第 1 页 / 共 34 页
第 2 页 / 共 34 页
第 3 页 / 共 34 页
第 4 页 / 共 34 页
第 5 页 / 共 34 页
第 6 页 / 共 34 页
第 7 页 / 共 34 页
第 8 页 / 共 34 页
第 9 页 / 共 34 页
第 10 页 / 共 34 页
第 11 页 / 共 34 页
第 12 页 / 共 34 页
第 13 页 / 共 34 页
第 14 页 / 共 34 页
第 15 页 / 共 34 页
第 16 页 / 共 34 页
第 17 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论-随机事件的独立性名词解释 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 18 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论-随机事件的独立性名词解释 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 19 页 / 共 34 页
第 20 页 / 共 34 页
第 21 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论-随机事件的独立性名词解释 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 22 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论-随机事件的独立性名词解释 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 23 页 / 共 34 页
第 24 页 / 共 34 页
第 25 页 / 共 34 页
第 26 页 / 共 34 页
第 27 页 / 共 34 页
第 28 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论-随机事件的独立性名词解释 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 29 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论-随机事件的独立性名词解释 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 30 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论-随机事件的独立性名词解释 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 31 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论-随机事件的独立性名词解释 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 32 页 / 共 34 页
第 33 页 / 共 34 页
第 34 页 / 共 34 页
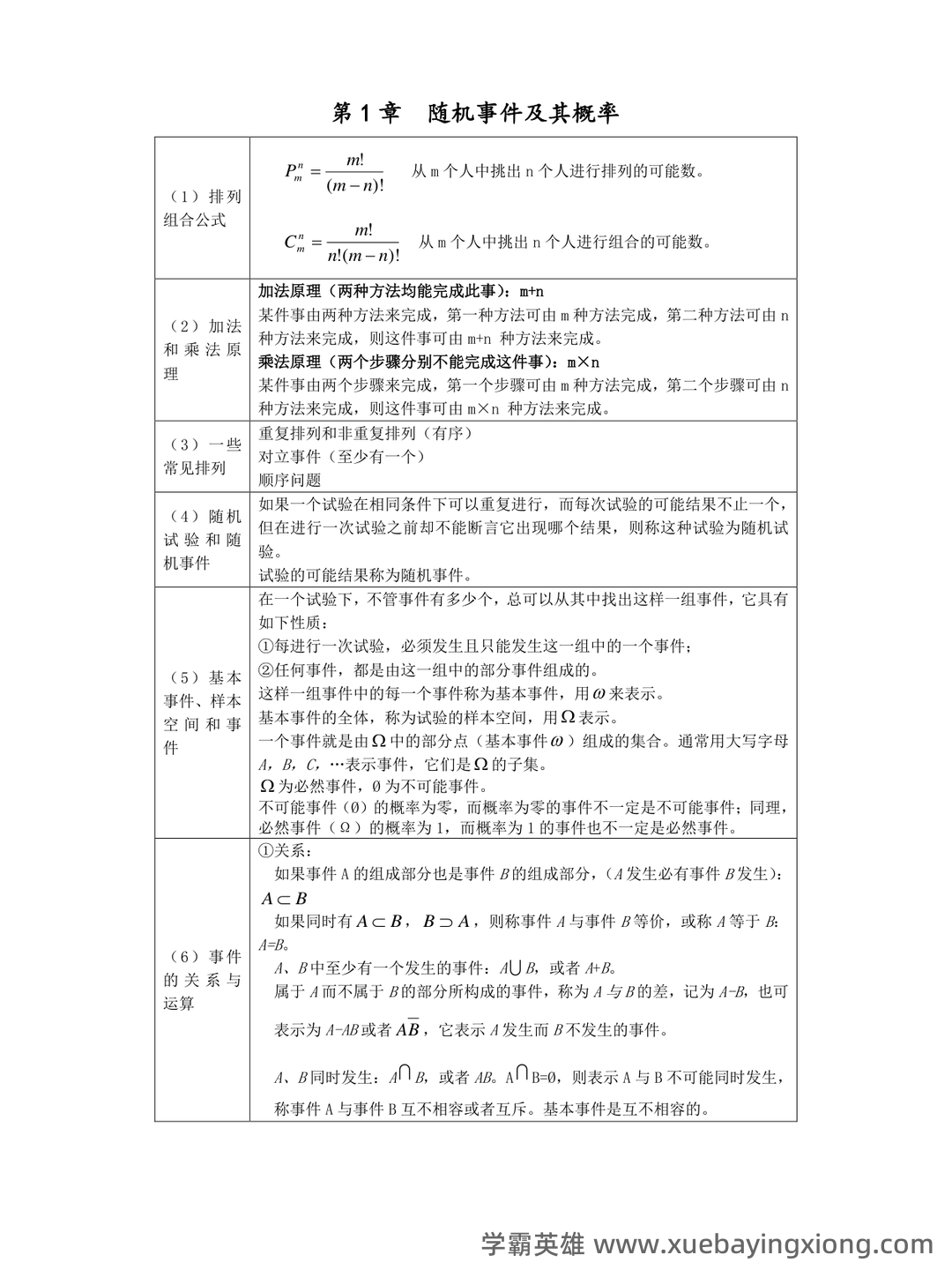
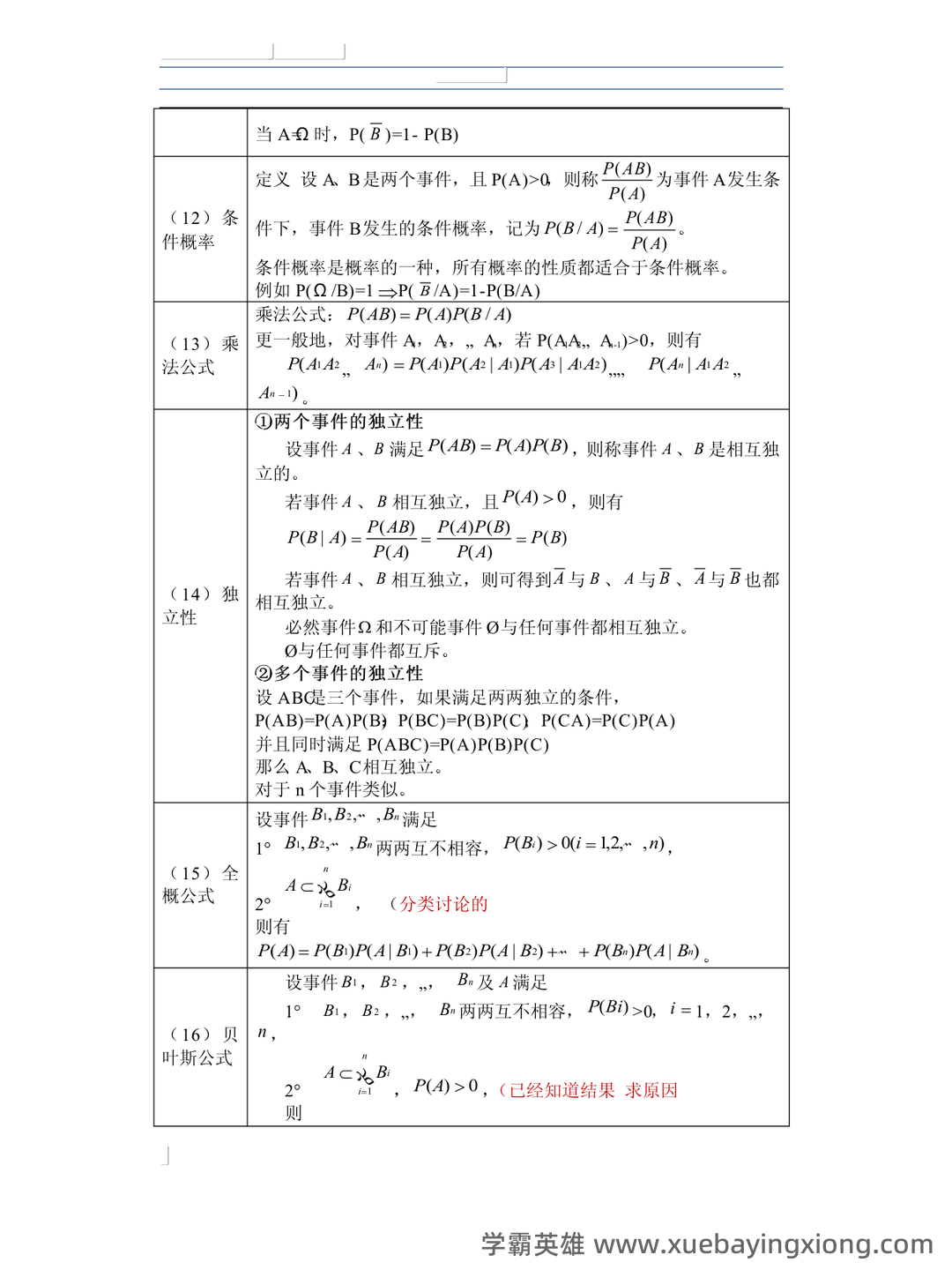
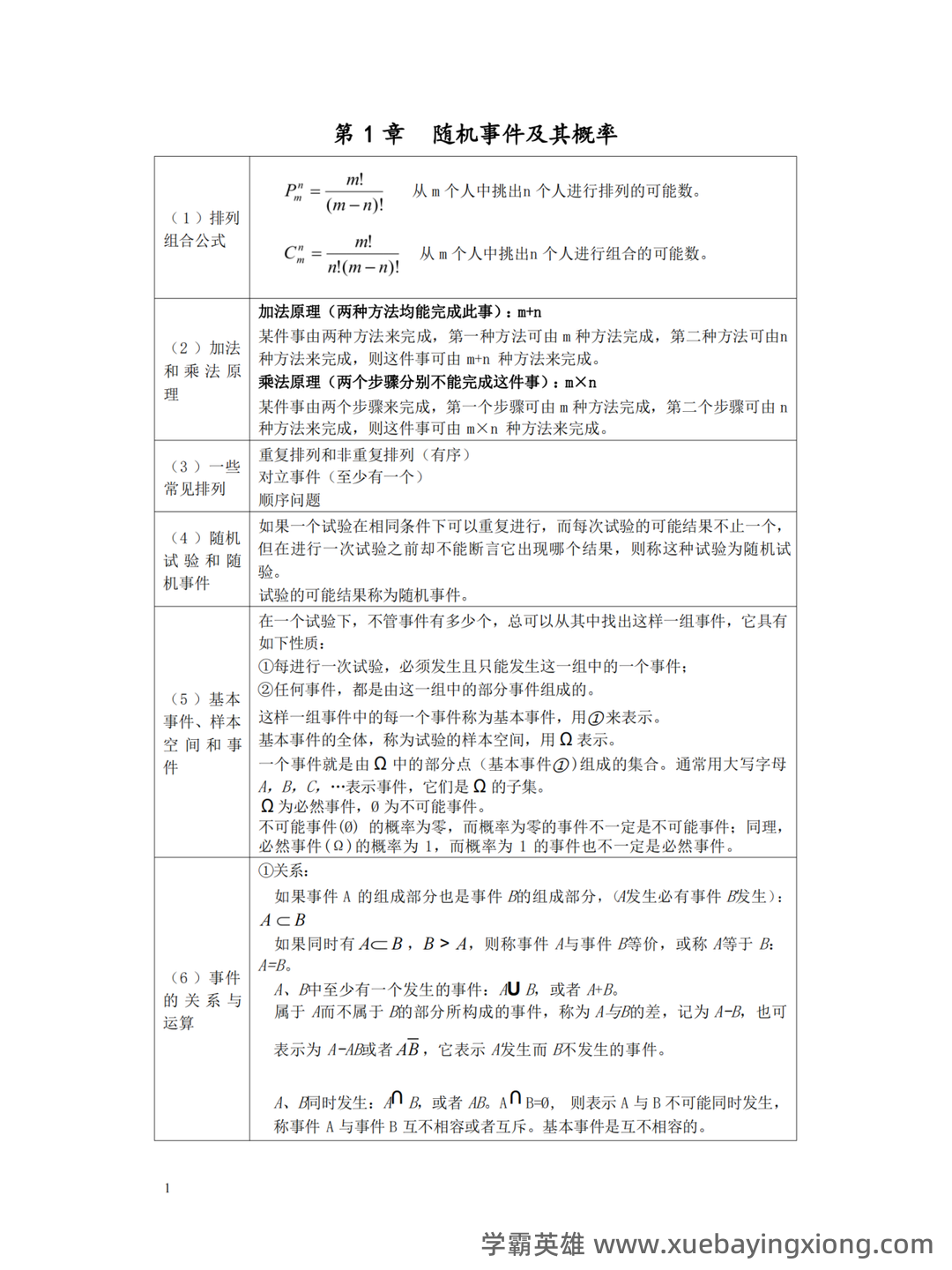
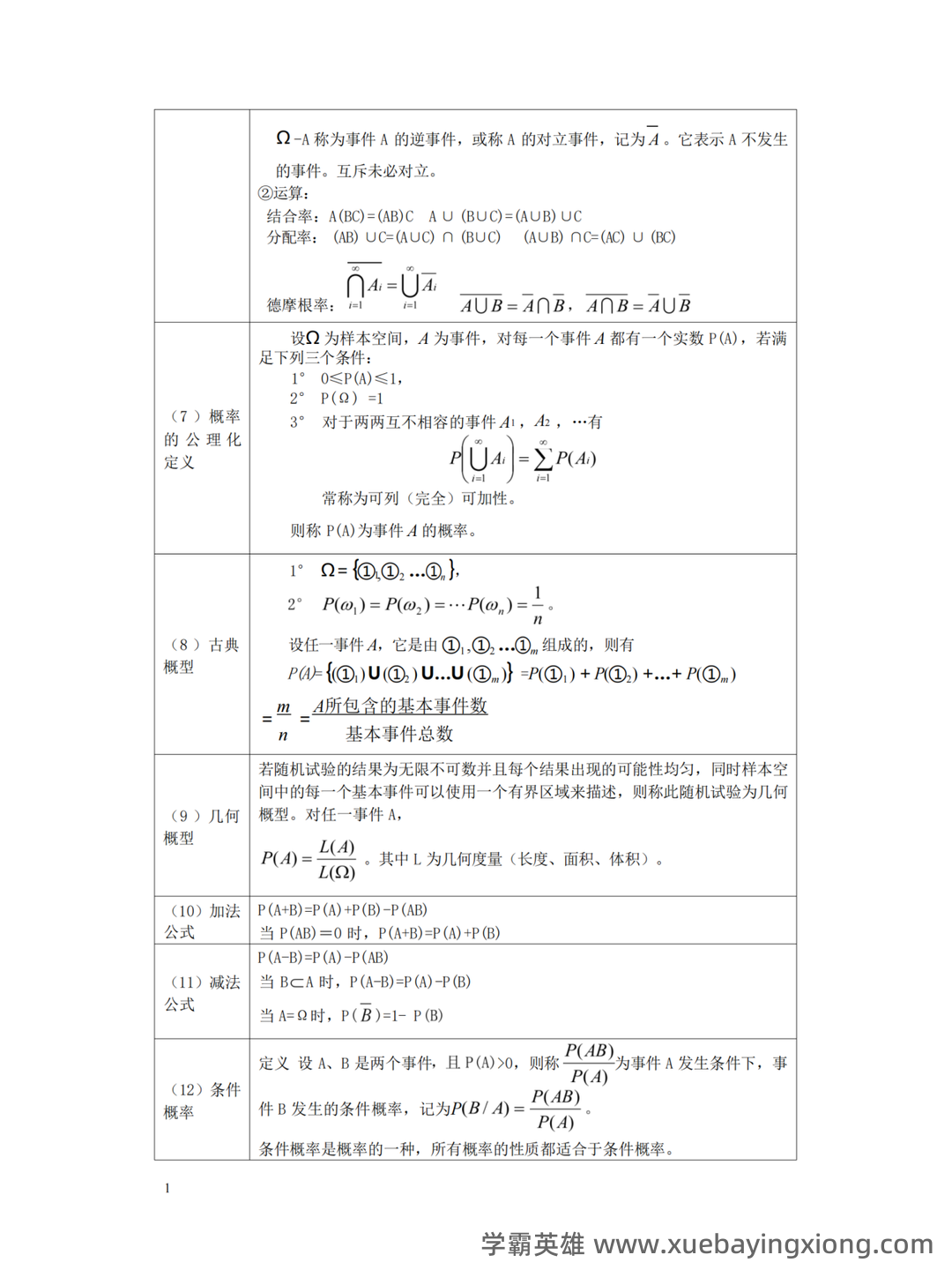
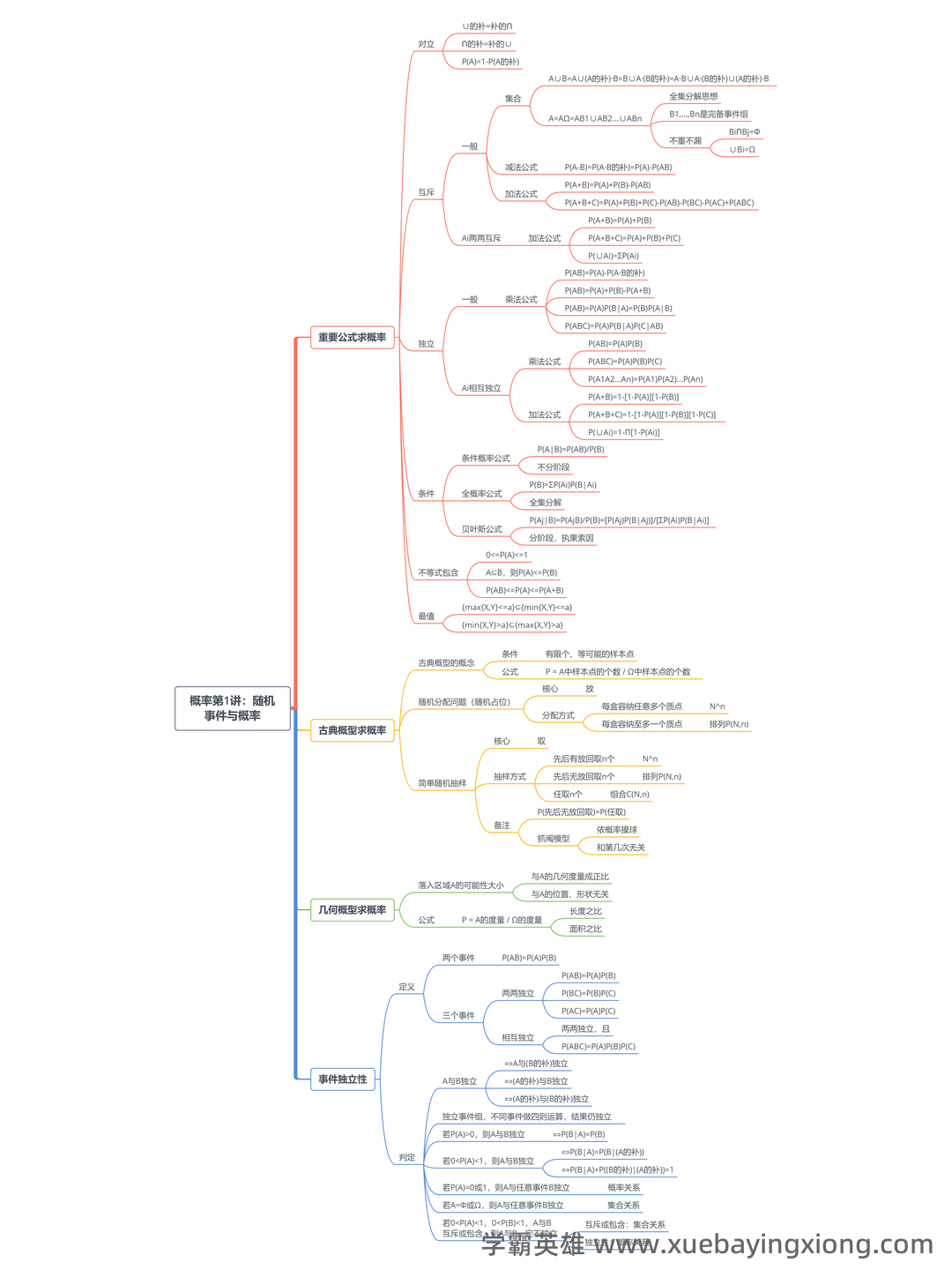
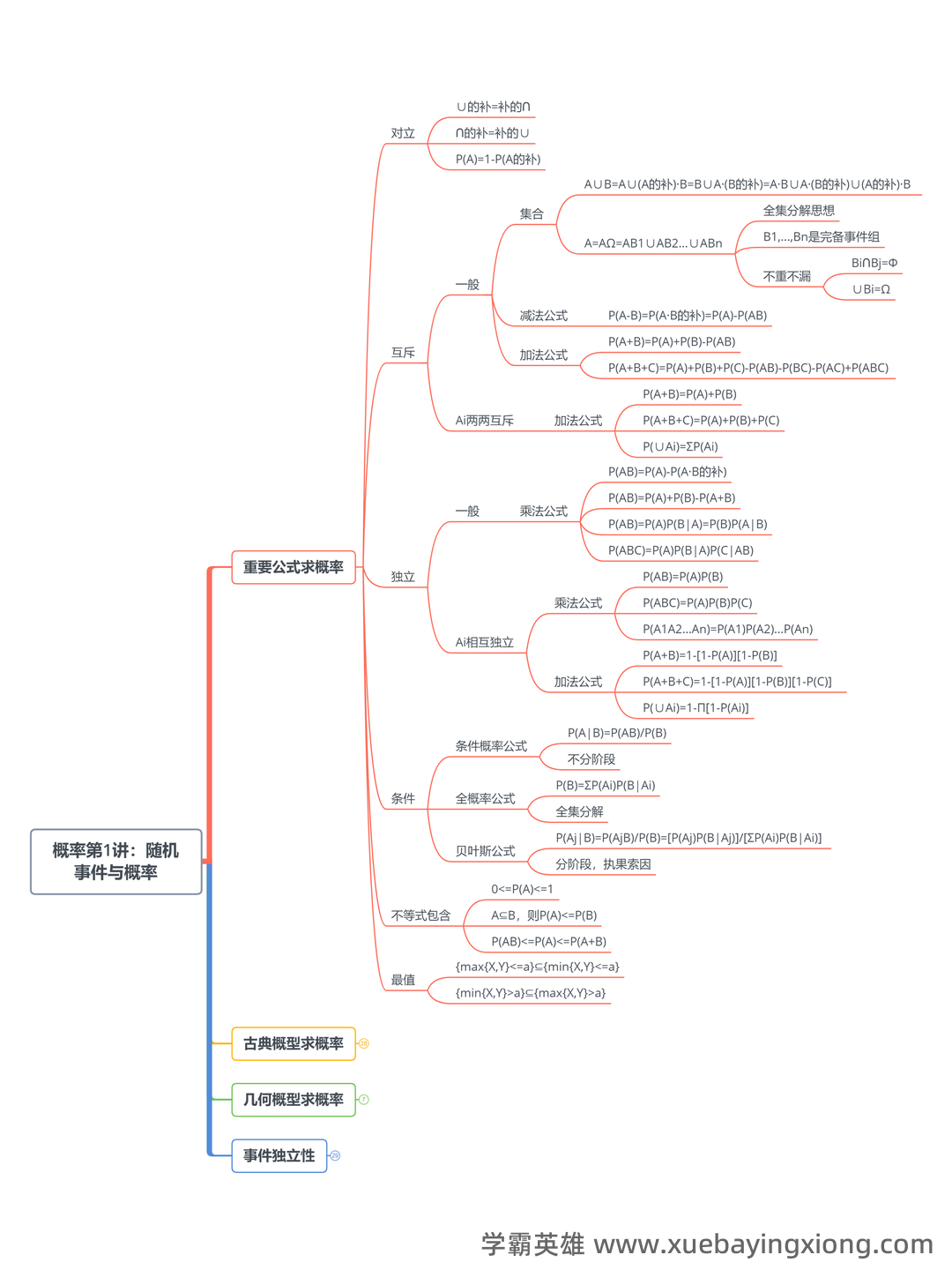
概率论-随机事件的独立性名词解释
--- 概率论，这个看似晦涩的学科，实际上就在我们生活的方方面面发挥着重要作用。它用数学的严谨逻辑去描述和理解不确定性，而“随机事件的独立性”则是概率论中一个至关重要的概念。 简单来说，如果两个事件是独立的，就意味着一个事件发生的概率，不会受到另一个事件发生或不发生的影响。换句话说，你知道一个事件发生的情况，就能完全确定另一个事件发生的概率，反之亦然。这与我们日常的直觉有些不同，毕竟很多时候，事物是相互关联的。 例如，抛硬币正面朝上和天气晴朗之间，通常是独立的。抛硬币的结果，并不取决于今天是否阳光明媚，反之亦然。当然，这需要基于足够多的样本数据来验证，避免出现偶然性的影响。 当然，现实生活中，很多事件并非完全独立。例如，股票价格的涨跌可能受到宏观经济形势的影响，而宏观经济形势又可能受到其他因素的影响。这种关联性构成了“相关性”，与“独立性”是完全相反的。 在概率论中，我们用“条件概率”来衡量事件之间的相关性。条件概率的计算公式可以帮助我们更好地理解和分析复杂系统中的相互关系。 理解独立性是学习概率论的基础，也是应用概率论解决实际问题的关键一步。 它不仅仅是数学概念，更是一种思维方式，帮助我们更好地认识和应对不确定性。
展开
概率论
2025-07-22
10次阅读