第 1 页 / 共 34 页
第 2 页 / 共 34 页
第 3 页 / 共 34 页
第 4 页 / 共 34 页
第 5 页 / 共 34 页
第 6 页 / 共 34 页
第 7 页 / 共 34 页
第 8 页 / 共 34 页
第 9 页 / 共 34 页
第 10 页 / 共 34 页
第 11 页 / 共 34 页
第 12 页 / 共 34 页
第 13 页 / 共 34 页
第 14 页 / 共 34 页
第 15 页 / 共 34 页
第 16 页 / 共 34 页
第 17 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "线性代数与概率论统计试卷模拟题及参考答案 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 18 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "线性代数与概率论统计试卷模拟题及参考答案 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 19 页 / 共 34 页
第 20 页 / 共 34 页
第 21 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "线性代数与概率论统计试卷模拟题及参考答案 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 22 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "线性代数与概率论统计试卷模拟题及参考答案 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 23 页 / 共 34 页
第 24 页 / 共 34 页
第 25 页 / 共 34 页
第 26 页 / 共 34 页
第 27 页 / 共 34 页
第 28 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "线性代数与概率论统计试卷模拟题及参考答案 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 29 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "线性代数与概率论统计试卷模拟题及参考答案 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 30 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "线性代数与概率论统计试卷模拟题及参考答案 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 31 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "线性代数与概率论统计试卷模拟题及参考答案 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 32 页 / 共 34 页
第 33 页 / 共 34 页
第 34 页 / 共 34 页
线性代数与概率论统计试卷模拟题及参考答案
线性代数与概率论统计试卷模拟题及参考答案 准备考试，你是不是也跟随着“概率论模拟题”的脚步，希望能通过练习来巩固知识，查漏补缺？ 线性代数和概率论是统计学和机器学习的基础，这套模拟试卷旨在帮助你更好地理解这两门学科的核心概念和方法。 首先，让我们回顾一下概率论的基本思想。概率论的核心在于用数学语言描述随机现象，并分析其规律。 从贝叶斯定理开始，理解事件发生的可能性，以及如何根据新的证据更新概率估计，是概率论的基础。 例如，在医学诊断中，医生会根据病人的症状、检查结果等信息，利用贝叶斯定理来计算患某种疾病的概率。 接下来，我们进入线性代数部分。 线性代数是概率论的数学工具。矩阵运算，向量空间，特征值和特征向量，这些概念在概率论中扮演着至关重要的角色。例如，在贝叶斯估计中，我们需要计算后验概率分布，这实际上涉及到矩阵的逆运算。 以下为试卷部分，包含题目和参考答案（仅供参考）： 题目一： (概率论) 假设一个袋子里有3个红球和5个白球，随机取出两个球，求取出的两个球颜色相同的概率。 参考答案： 该问题可以使用组合的知识来解决。 先从总球数中选取2个球的方法有C(8,2) = 28种。 取到两个红球的方法有C(3,2) = 3种。 所以概率为 3/28 。 题目二： (线性代数) 给定矩阵A = [[2, 1], [1, 1]]，求其行列式和逆矩阵。 参考答案： 行列式为 21 - 11 = 1。 逆矩阵为 (1/1) [[1, -1], [-1, 2]] = [[1, -1], [-1, 2]] 。 题目三： (统计学交叉) 在贝叶斯估计中，如果先验概率分布为高斯分布，那么后验概率分布也通常是高斯分布。请简述这种关系背后的数学原理。 参考答案： 这基于高斯分布的性质，以及贝叶斯定理的推导过程。具体来说，如果先验分布是高斯分布，并且似然函数也与高斯分布相关，则后验分布也会是高斯分布，并且其均值为先验均值的加权平均，方差为先验方差的加权平均，权重由先验概率和似然函数决定。 希望这套模拟试卷能帮助你更好地理解线性代数和概率论的关联，并为你的考试做好充分的准备！记住，熟能生巧，多做题才能真正掌握这些重要的知识。
展开
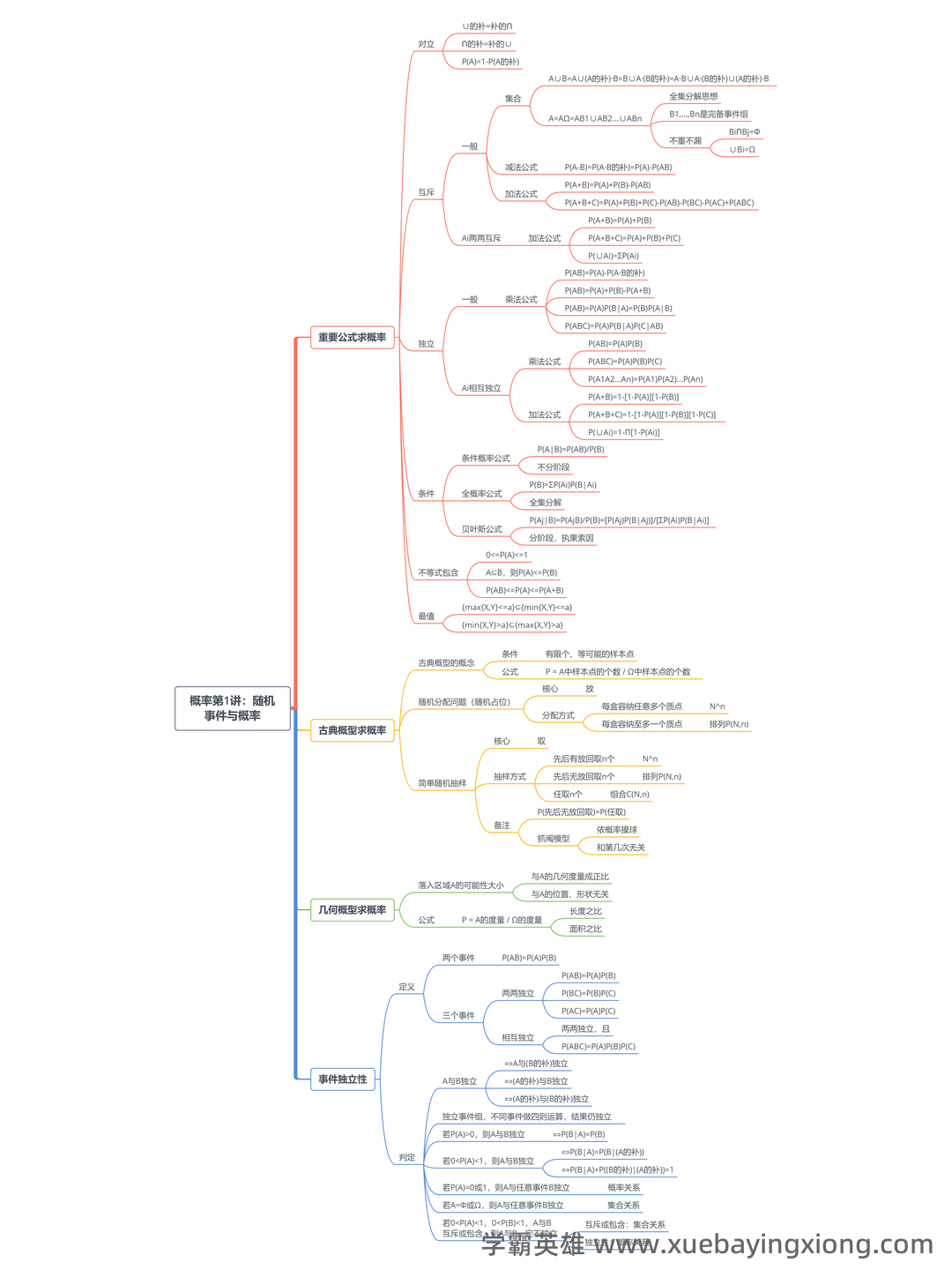
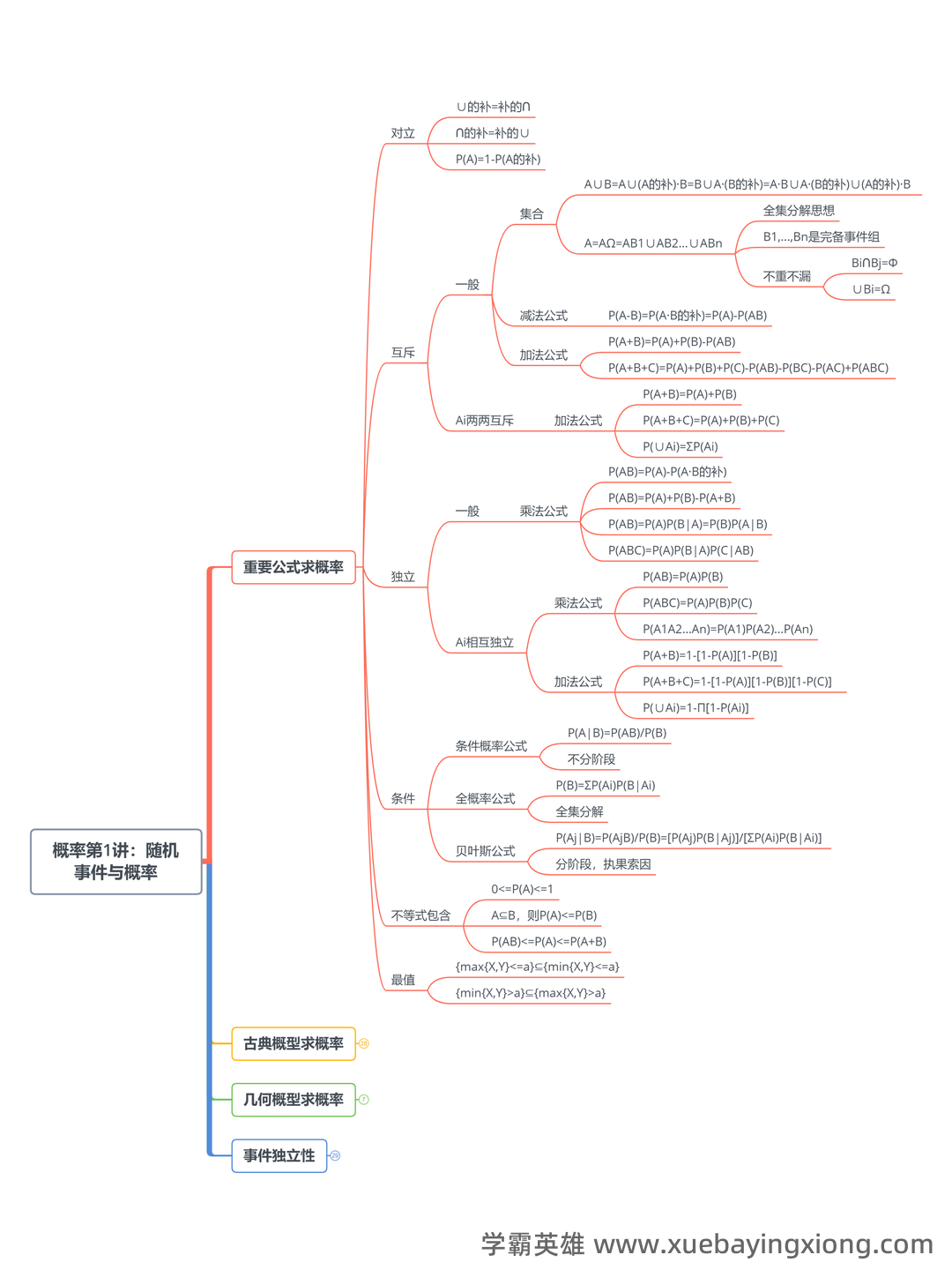
概率论
2025-07-22
9次阅读