第 1 页 / 共 34 页
第 2 页 / 共 34 页
第 3 页 / 共 34 页
第 4 页 / 共 34 页
第 5 页 / 共 34 页
第 6 页 / 共 34 页
第 7 页 / 共 34 页
第 8 页 / 共 34 页
第 9 页 / 共 34 页
第 10 页 / 共 34 页
第 11 页 / 共 34 页
第 12 页 / 共 34 页
第 13 页 / 共 34 页
第 14 页 / 共 34 页
第 15 页 / 共 34 页
第 16 页 / 共 34 页
第 17 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论速成复习指南：关键知识点总结 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 18 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论速成复习指南：关键知识点总结 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 19 页 / 共 34 页
第 20 页 / 共 34 页
第 21 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论速成复习指南：关键知识点总结 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 22 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论速成复习指南：关键知识点总结 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 23 页 / 共 34 页
第 24 页 / 共 34 页
第 25 页 / 共 34 页
第 26 页 / 共 34 页
第 27 页 / 共 34 页
第 28 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论速成复习指南：关键知识点总结 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 29 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论速成复习指南：关键知识点总结 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 30 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论速成复习指南：关键知识点总结 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 31 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论速成复习指南：关键知识点总结 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 32 页 / 共 34 页
第 33 页 / 共 34 页
第 34 页 / 共 34 页
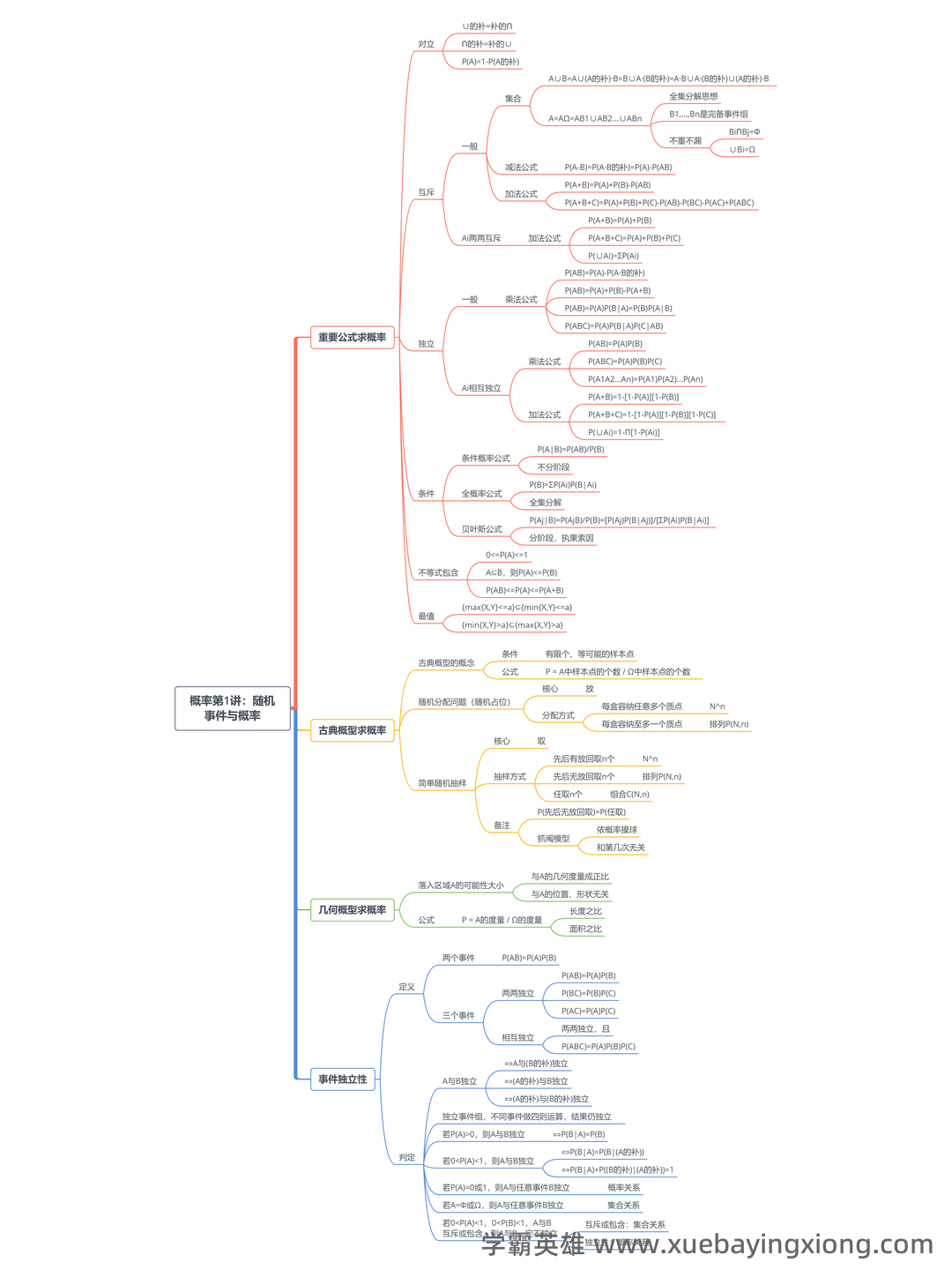
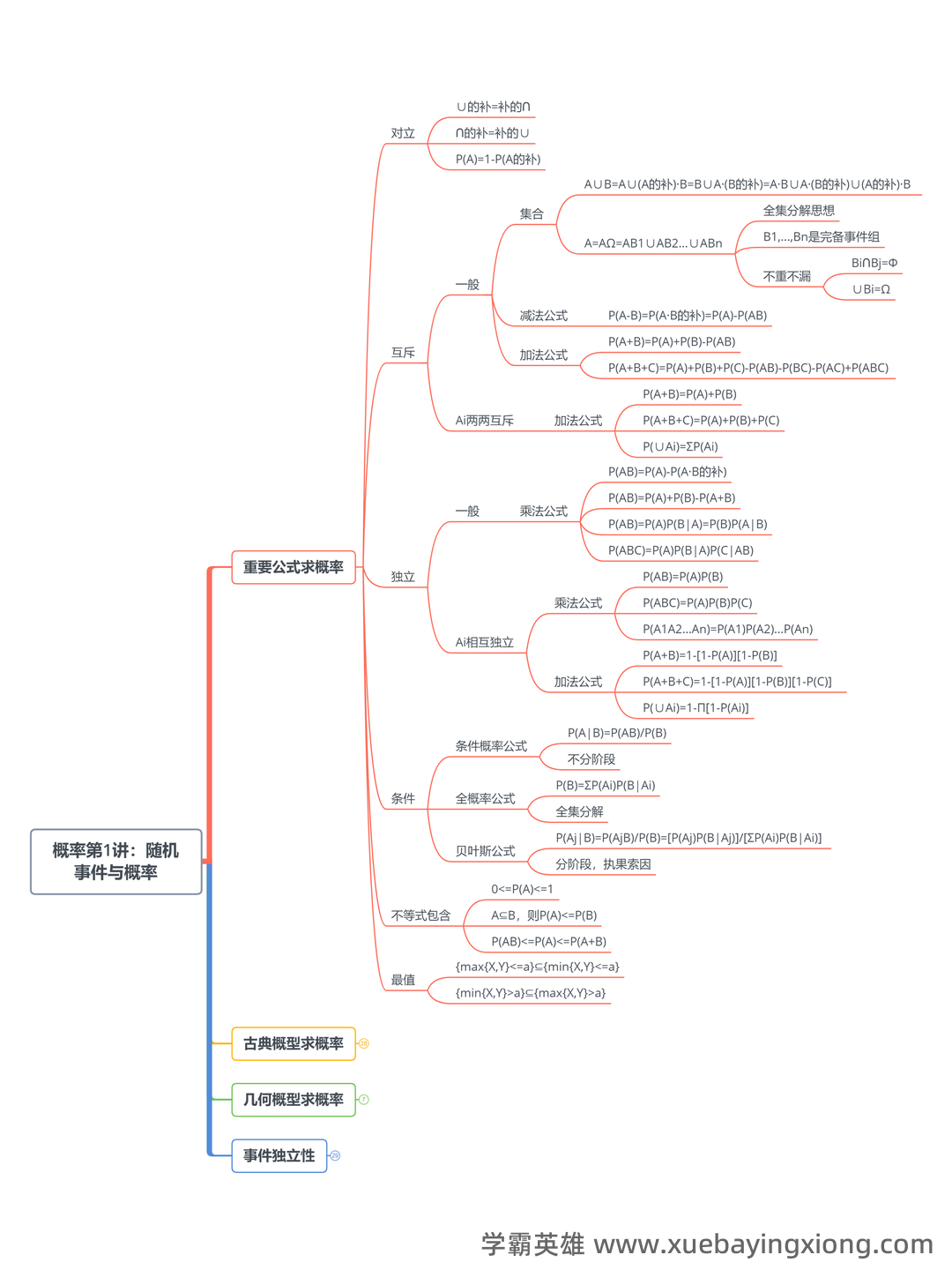
概率论速成复习指南：关键知识点总结
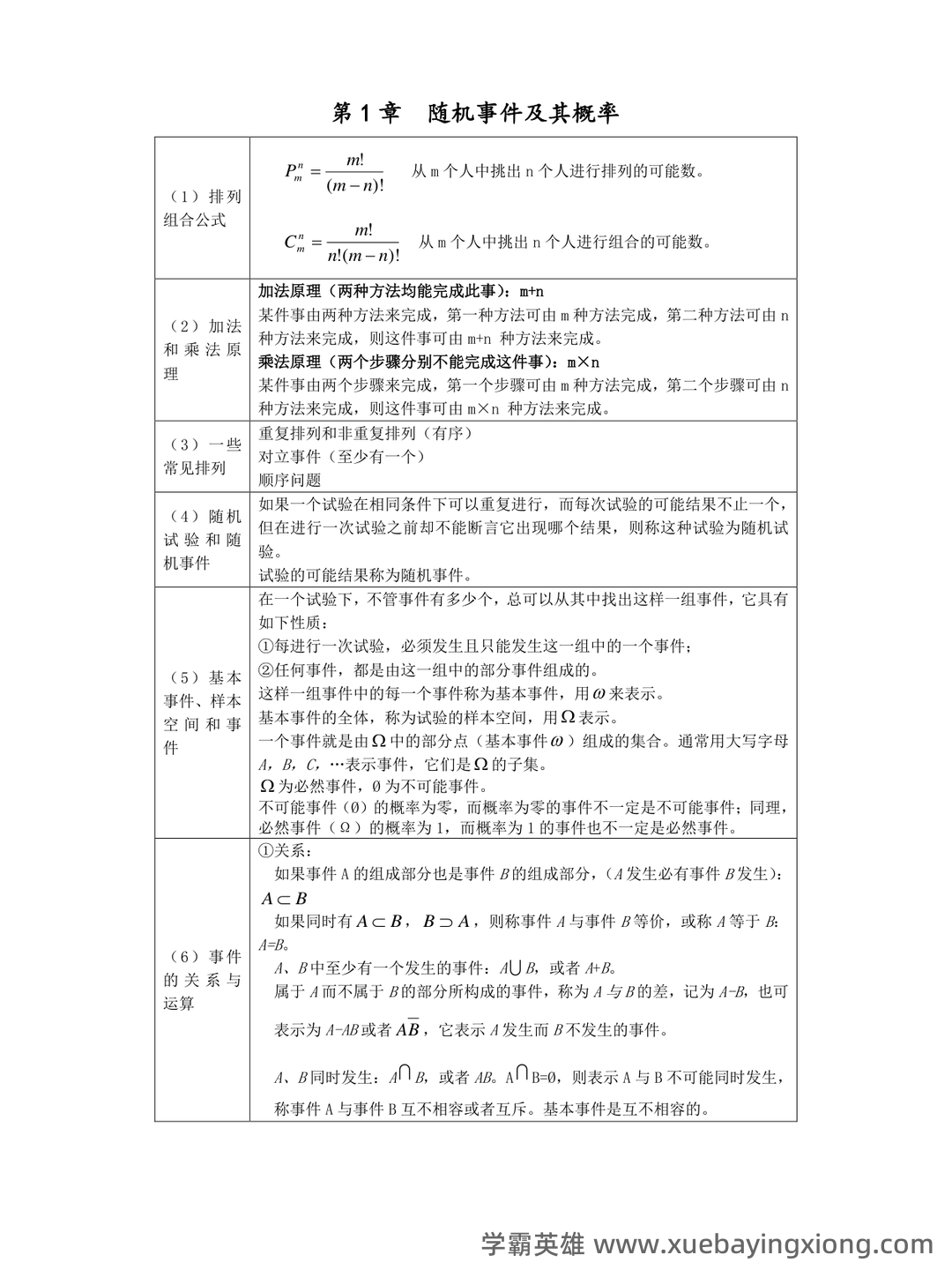
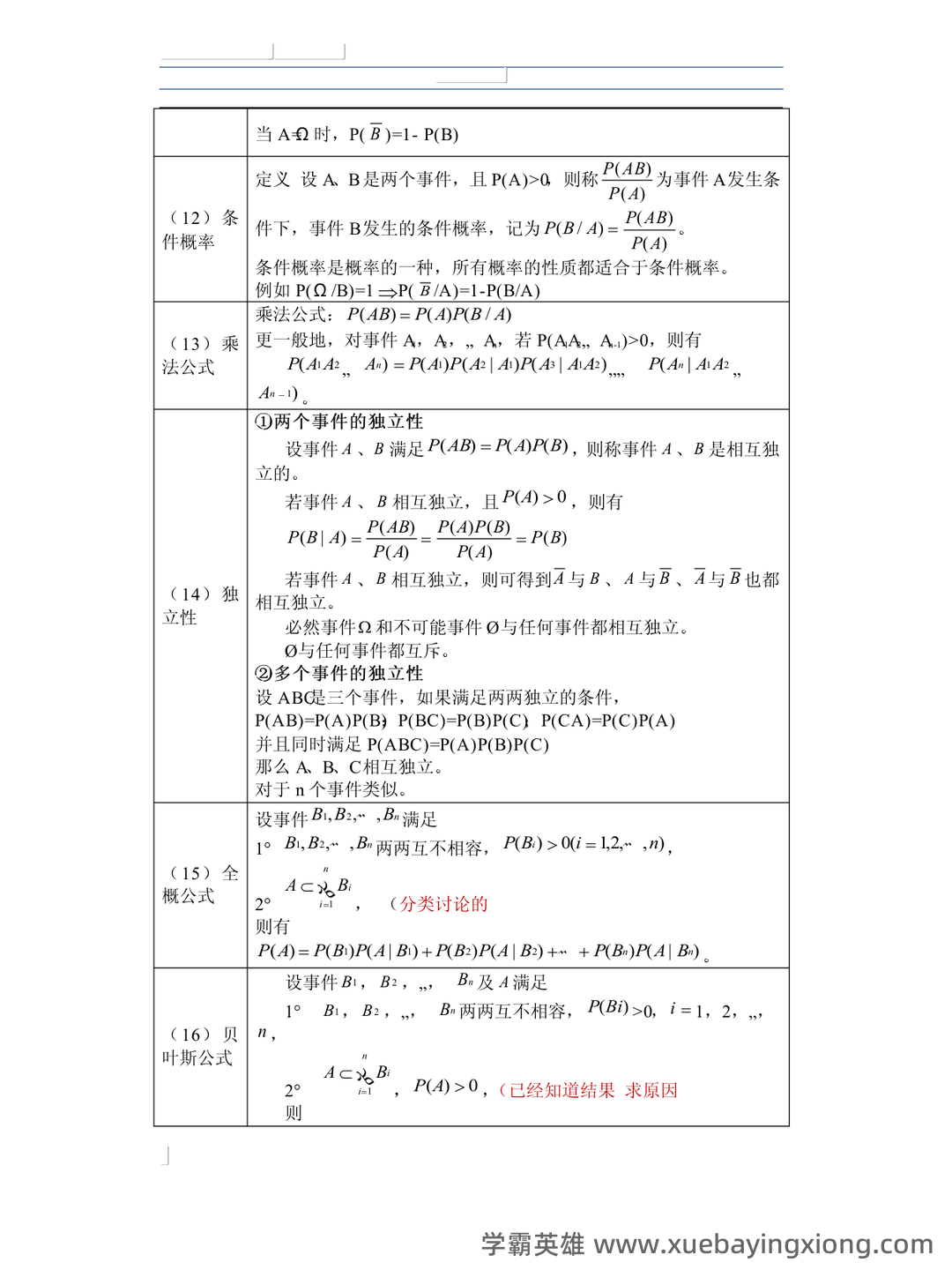
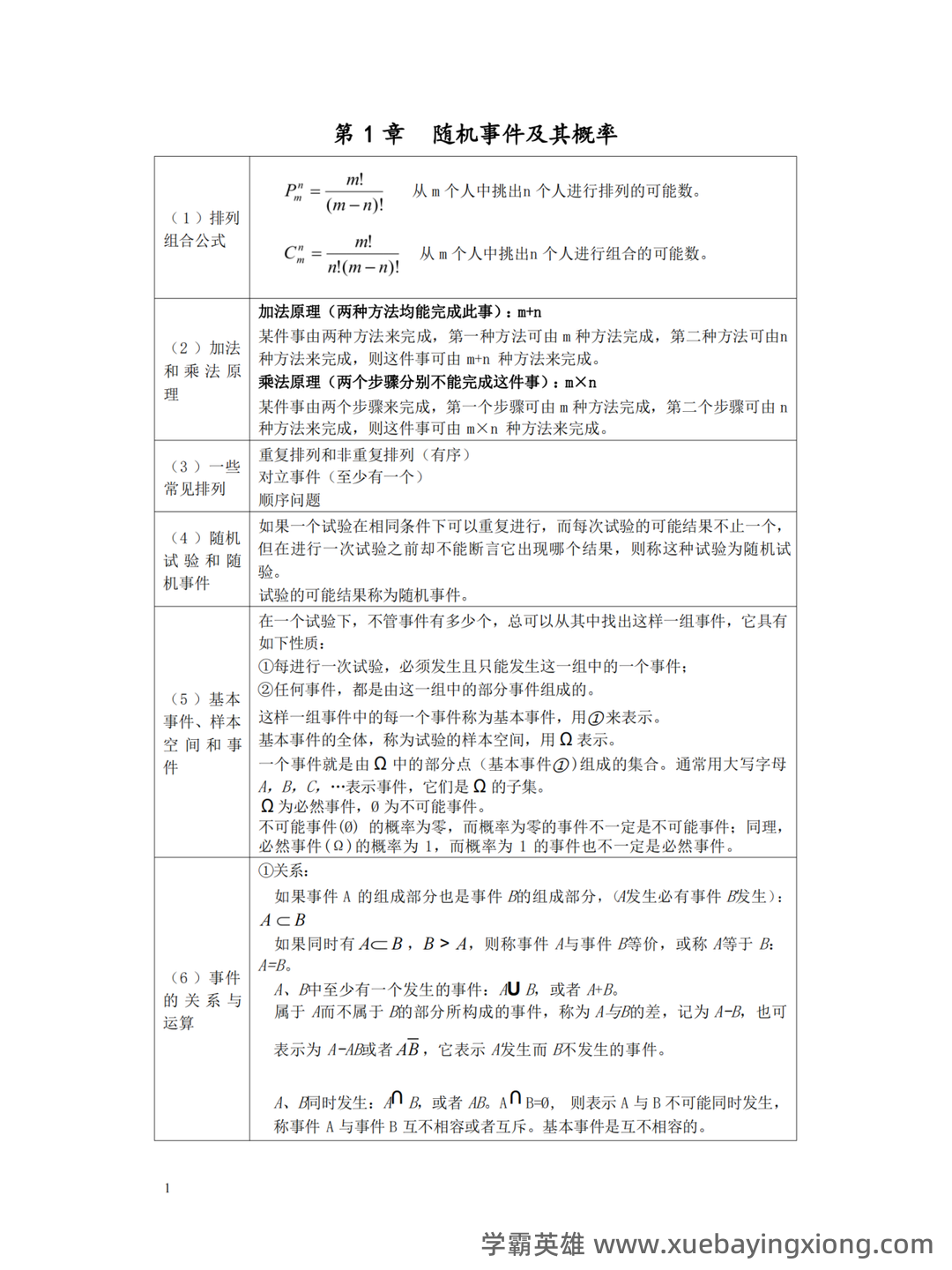
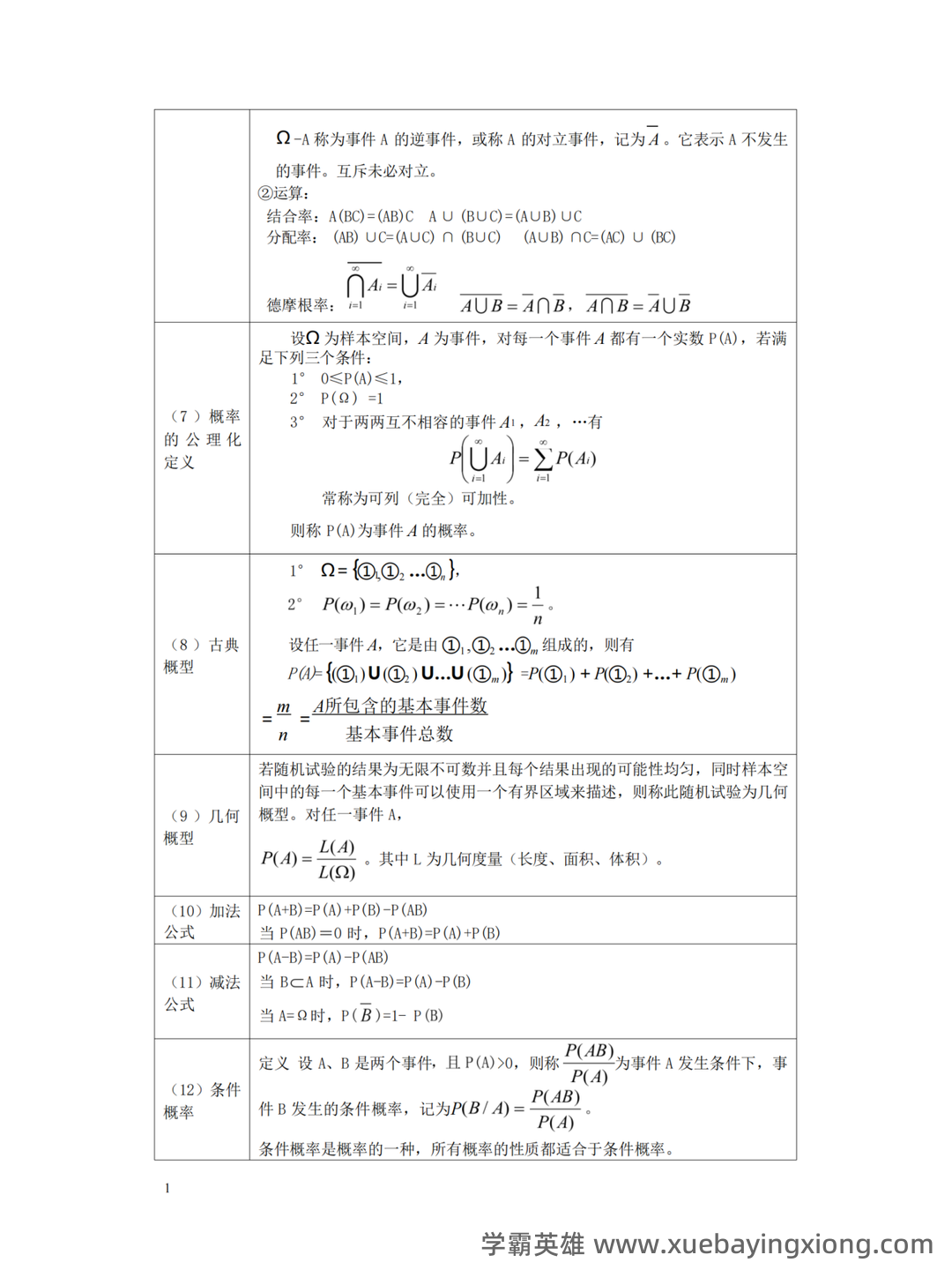
概率论速成复习指南：关键知识点总结 概率论是理解和预测不确定性事件的基础。对于需要快速复习的同学，掌握以下关键知识点至关重要。 1. 基本概念：概率的定义与计算 概率是指一个事件发生的可能性。简单的概率计算公式是： P(事件) = (事件中理想情况的数量) / (所有可能情况的总数)。例如，一枚公平的硬币落地正面朝上概率为 1/2。 2. 常用概率分布 伯努利分布： 用于描述只有两种可能结果（成功或失败）的事件，例如抛硬币或掷骰子。 二项分布： 用于描述重复进行多次伯努利试验的次数达到特定次数的概率。 正态分布： 广泛应用于自然科学和社会科学中，描述数据的集中趋势。 3. 条件概率与独立性 条件概率： 在已知某个事件已经发生的条件下，另一个事件发生的概率。公式为：P(A|B) = P(A∩B) / P(B)。 独立事件： 如果事件A的发生不影响事件B发生的概率，则A和B是独立的。 4. 常用定理与公式 全概率公式： P(A) = P(A|B1)P(B1) + P(A|B2)P(B2) + ... + P(A|Bn)P(Bn) （对所有可能的分离事件A的概率进行加权求和）。 贝叶斯定理： 用于计算在已知一些证据的情况下，某个假设的概率。 掌握这些核心概念和公式，能够快速回顾概率论的关键内容，为后续学习和应用打下坚实基础。对于需要短期内复习概率论的同学，建议重点关注以上内容，并结合实例进行练习。
展开
概率论
2025-04-17
16次阅读