机器学习相关 概率论重点笔记_joint probability怎么算 - 00_《概率论与数理统计》复习资料_封面首图_学霸英雄_www.xuebayingxiong.com
第 1 页 / 共 34 页
获取资料
学霸英雄

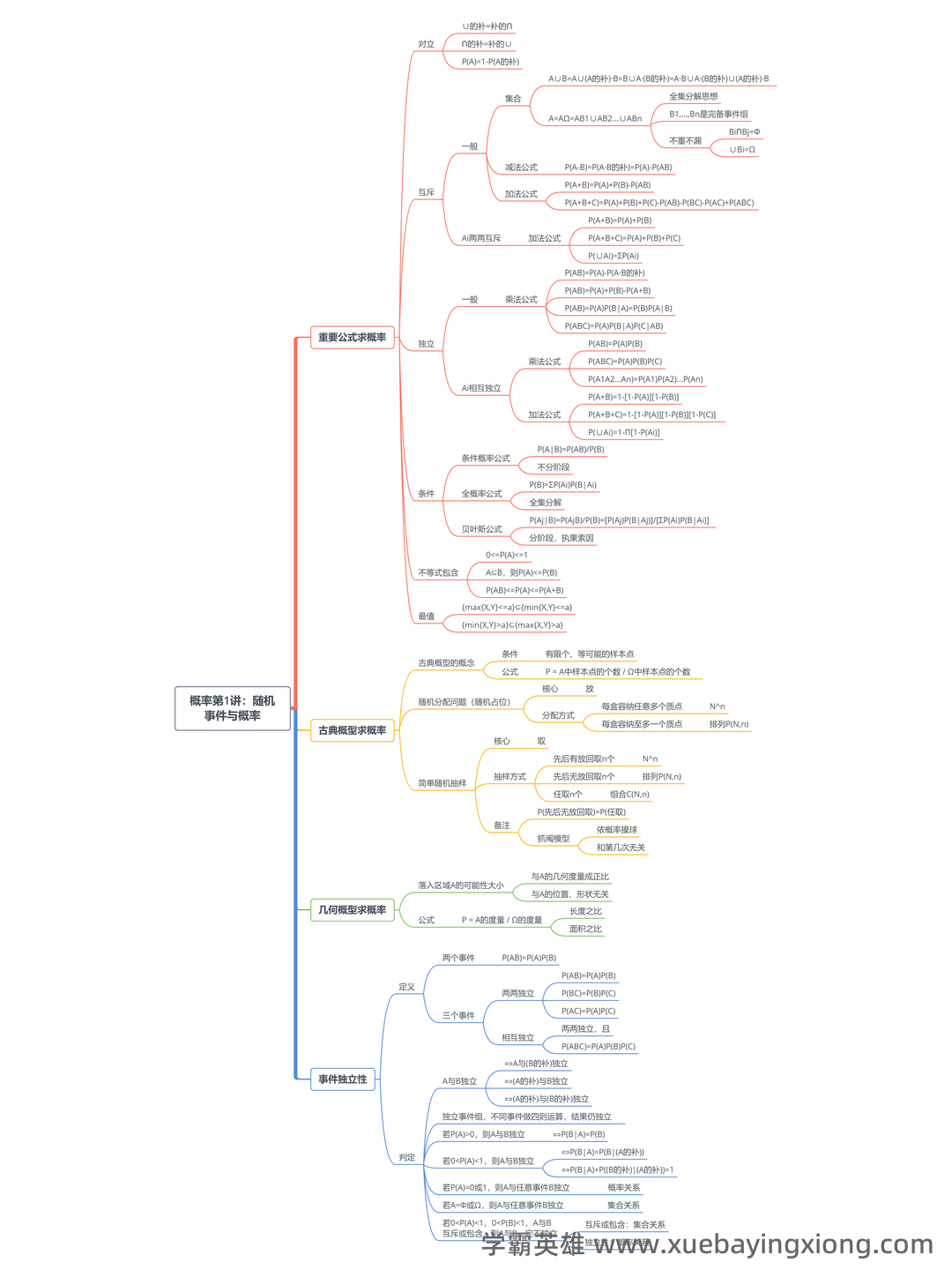
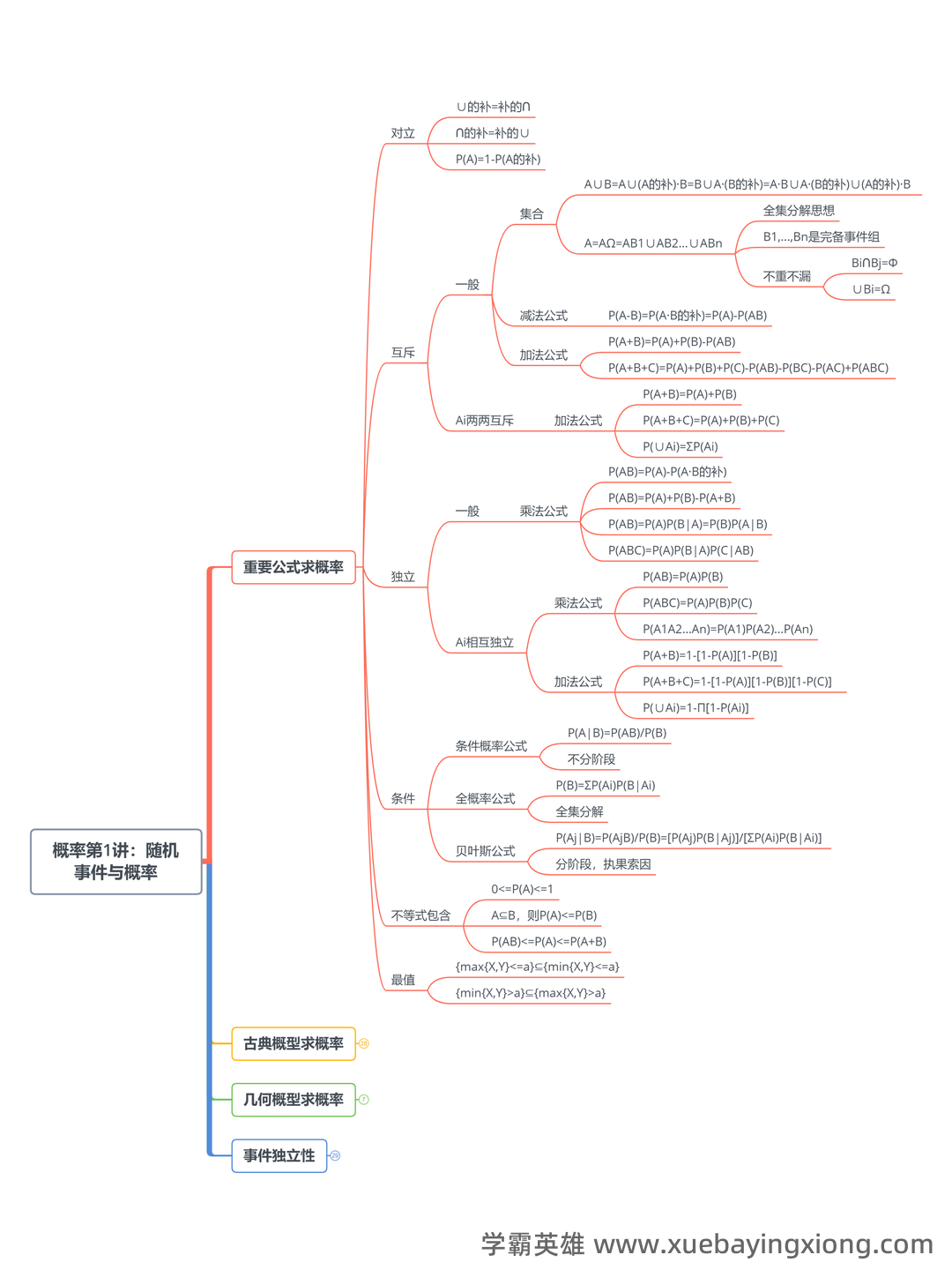
机器学习相关 概率论重点笔记_joint probability怎么算

机器学习相关 概率论重点笔记_joint probability怎么算 概率论是机器学习的基石，而当谈到联合概率的计算，更是深入理解模型运作的关键。 简单来说，概率论的核心在于描述不确定性，而联合概率则精确地捕捉了多个事件同时发生的可能性。 无论是贝叶斯定理还是各种生成模型，都离不开对联合概率的巧妙应用。 联合概率，记作P(A, B)，表示事件A和事件B同时发生的概率。 这与我们通常理解的条件概率有所不同。 条件概率是已知某个事件已经发生的情况下，另一个事件发生的概率，而联合概率则直接衡量了两个事件共同出现的情况。 记住这一点非常重要！ 那么，如何计算联合概率呢？ 最基本的方法是利用频率派生。 如果在大量试验中，事件A和B同时发生的次数与它们各自发生的次数相比较，那么它们的联合概率就可以近似地由比例关系来确定。 也就是说： P(A, B) = P(A) P(B|A) ，其中 P(B|A) 是在A已经发生的条件下，B发生的概率。 当然，实际应用中，很多情况下我们无法直接获得联合概率，而是需要通过其他方法进行推导。 例如，我们可以利用全概率公式来分解复杂的情况，或者采用各种蒙特卡洛模拟等方法进行估计。 搞清楚 P(A, B) 与 P(A|B) 和 P(B) 的关系，是解决联合概率问题的关键。 总而言之，联合概率的概念及其计算方法，是机器学习中一个至关重要的组成部分。 掌握了它的精髓，你才能更深入地理解和应用各种机器学习算法。 展开
#概率论笔记 #概率论重点 #jointprobability #概率论公式 #机器学习概率论 #概率论讲解 #概率论教程
概率论
2025-07-22
12次阅读

相关文章

概率论—期末复习笔记（自用）

概率论和数理统计期末考试题及答案（最全）

怎么学好概率论，期末考试83分以上？