第 1 页 / 共 34 页
第 2 页 / 共 34 页
第 3 页 / 共 34 页
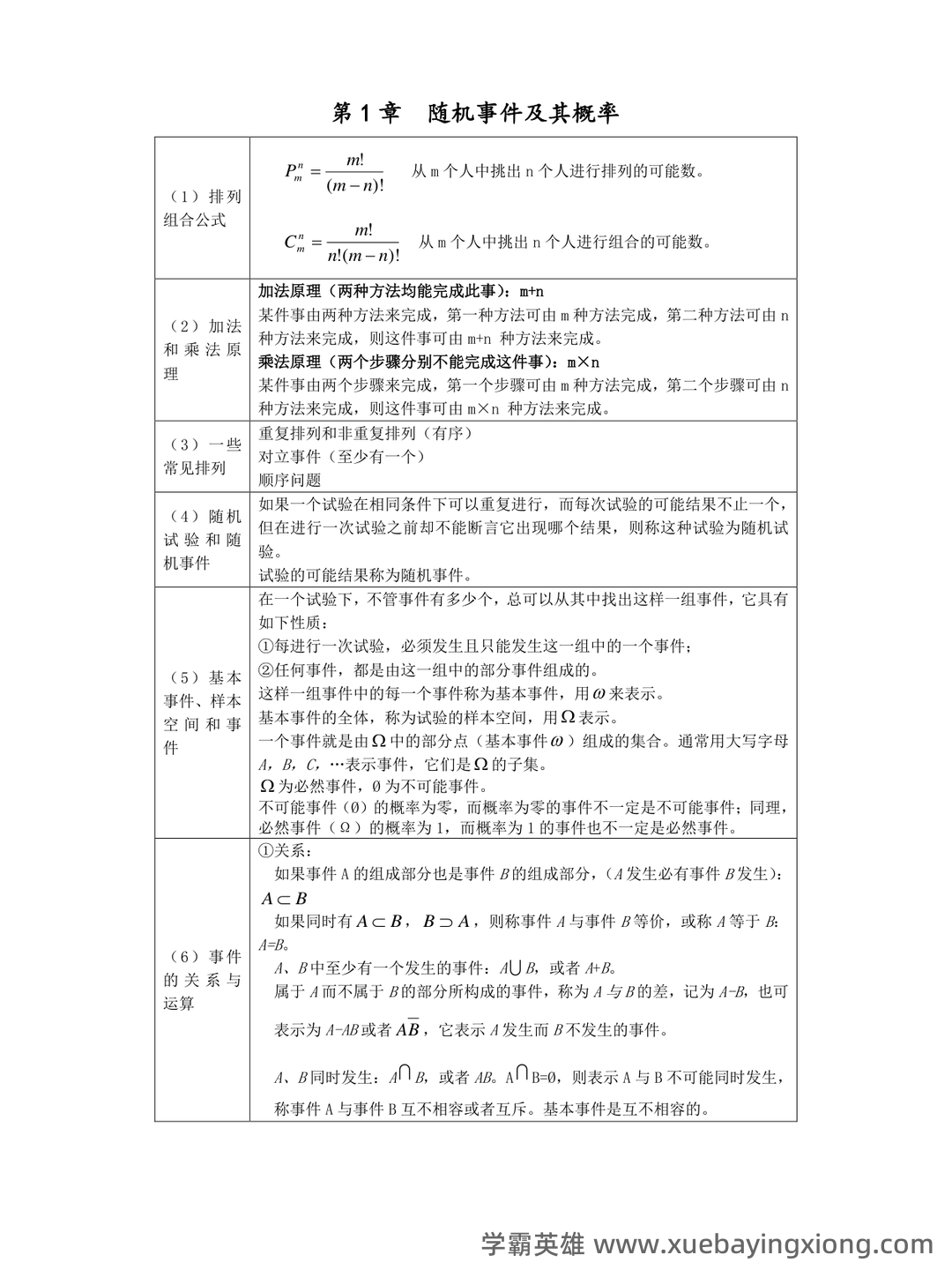
第 4 页 / 共 34 页
第 5 页 / 共 34 页
第 6 页 / 共 34 页
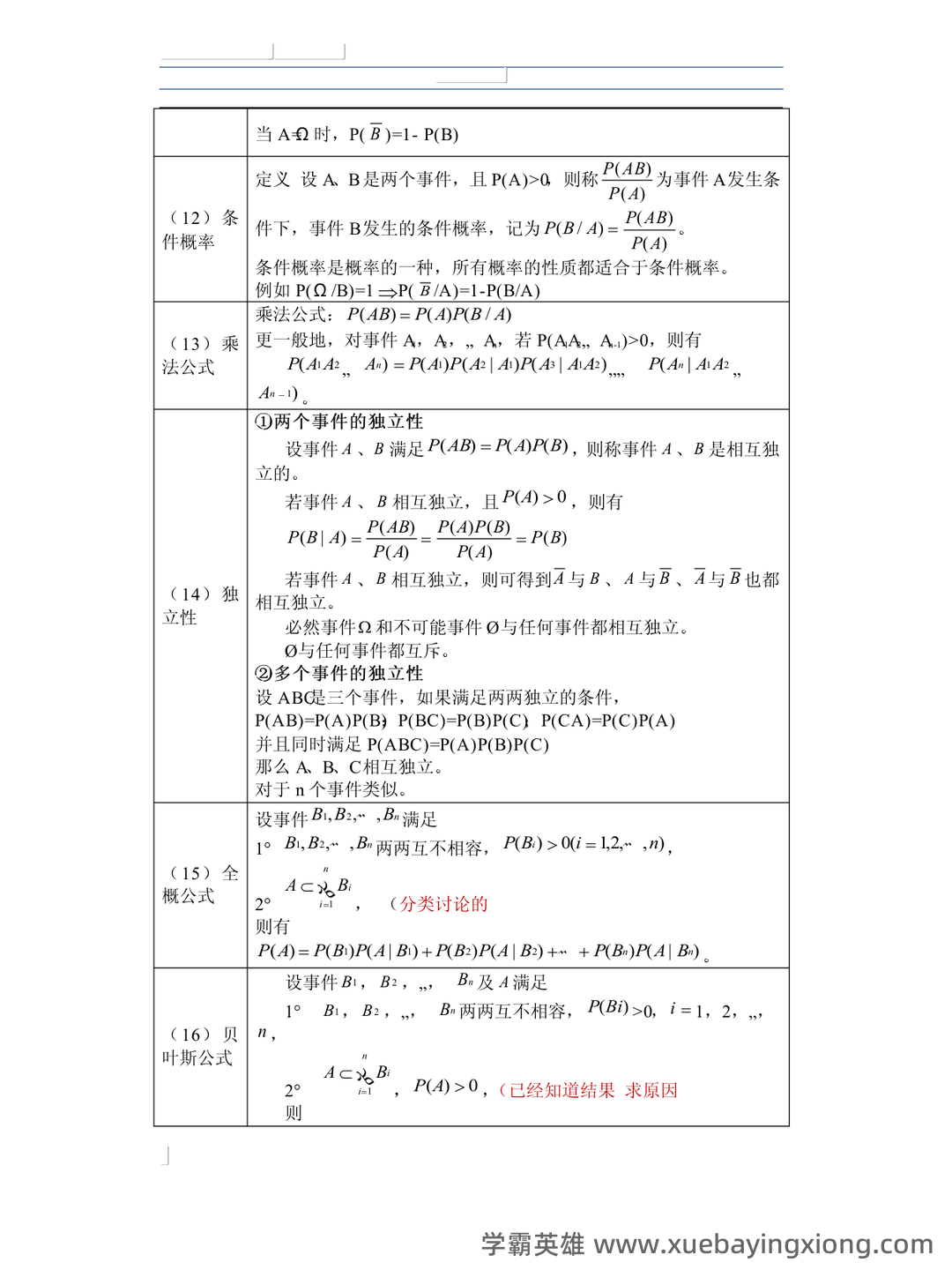
第 7 页 / 共 34 页
第 8 页 / 共 34 页
第 9 页 / 共 34 页
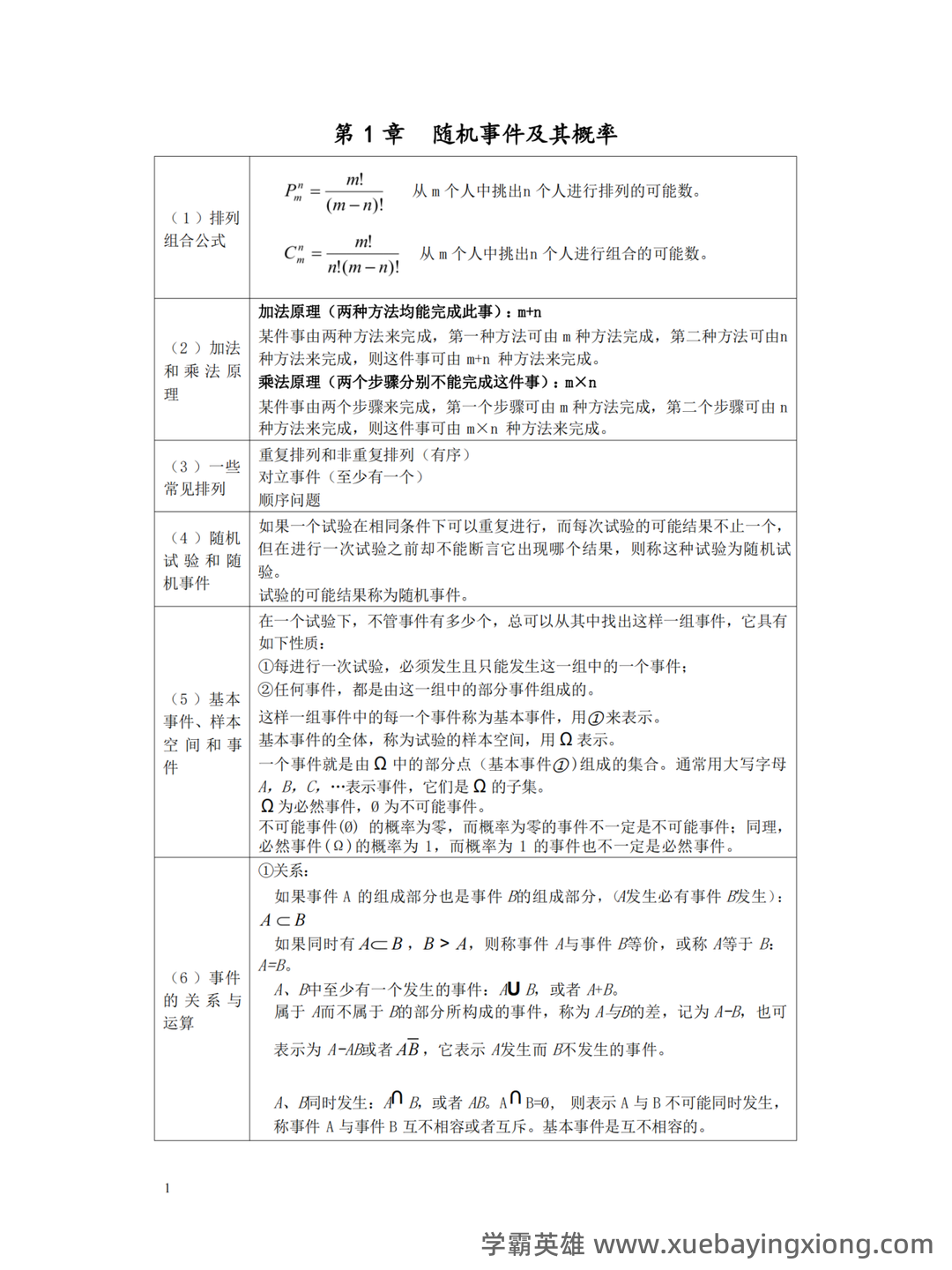
第 10 页 / 共 34 页
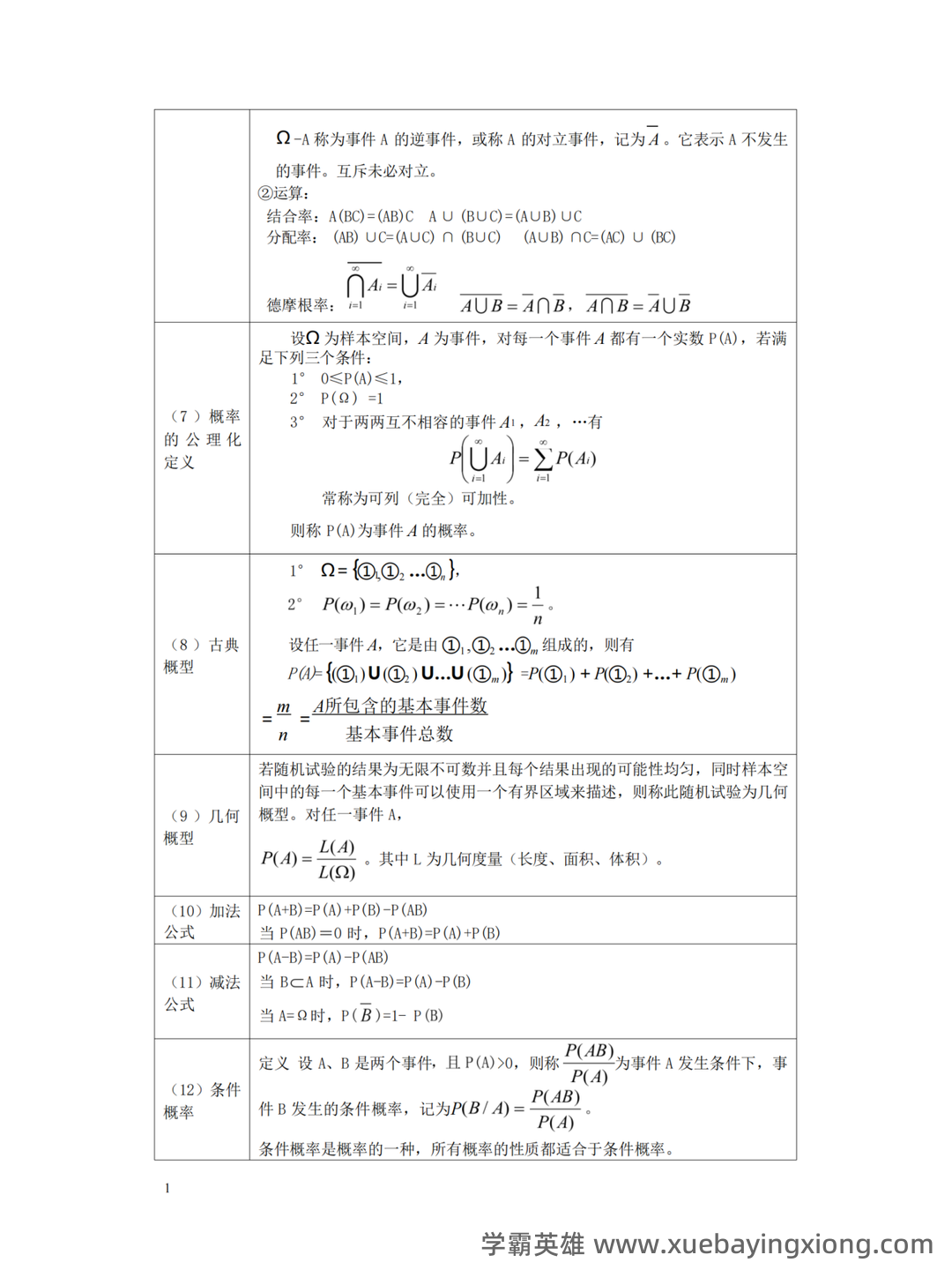
第 11 页 / 共 34 页
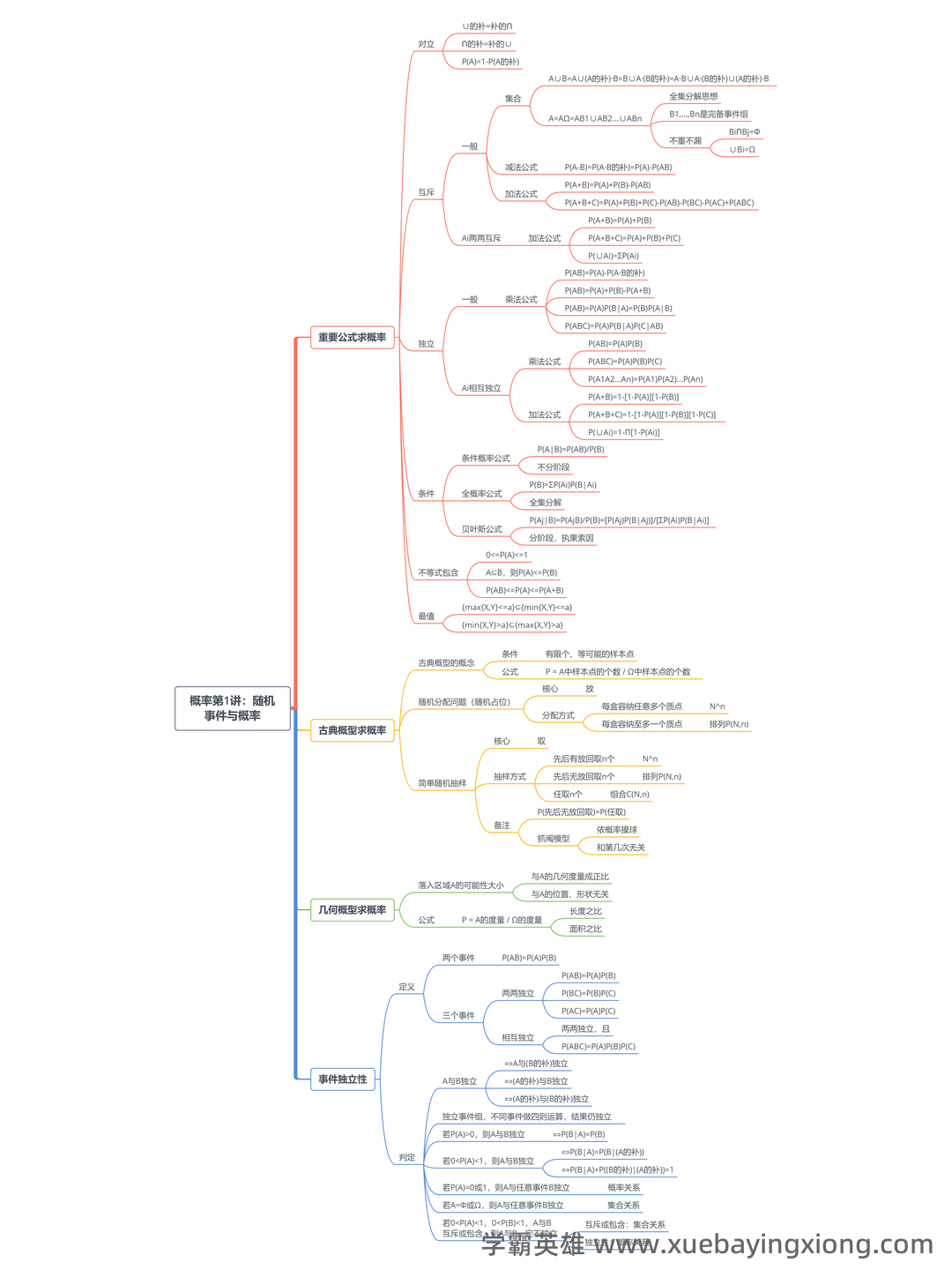
第 12 页 / 共 34 页
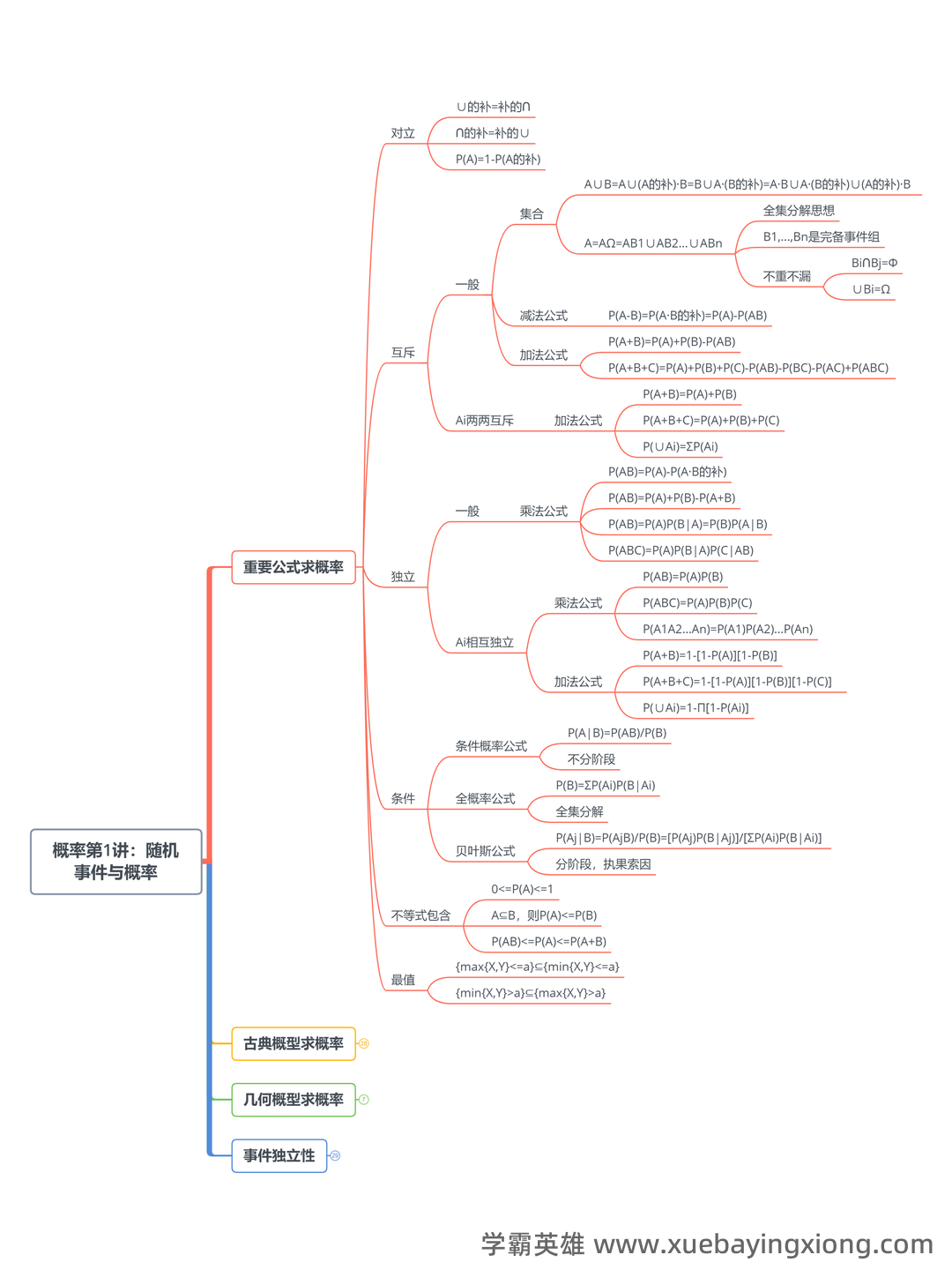
第 13 页 / 共 34 页
第 14 页 / 共 34 页
第 15 页 / 共 34 页
第 16 页 / 共 34 页
第 17 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论总复习（Probability） - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 18 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论总复习（Probability） - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 19 页 / 共 34 页
第 20 页 / 共 34 页
第 21 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论总复习（Probability） - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 22 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论总复习（Probability） - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 23 页 / 共 34 页
第 24 页 / 共 34 页
第 25 页 / 共 34 页
第 26 页 / 共 34 页
第 27 页 / 共 34 页
第 28 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论总复习（Probability） - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 29 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论总复习（Probability） - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 30 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论总复习（Probability） - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 31 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论总复习（Probability） - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 32 页 / 共 34 页
第 33 页 / 共 34 页
第 34 页 / 共 34 页
概率论总复习（Probability）
概率论总复习（Probability） 概率论，看似抽象，实则贯穿于我们生活的方方面面。从天气预报到股票市场，甚至我们日常的决策，都离不开概率的考量。 简单来说，它研究的是随机事件发生的可能性。 就像抛硬币，正面朝上的概率是1/2，反面朝上的概率也是1/2，这两者互为对立，且概率之和必然等于1。 核心概念之一是“随机变量”。 随机变量是指在随机实验中，可以取得各种可能值的变量。 比如，掷骰子，点数1到6的概率，都可以用随机变量来描述。 随机变量可以分为离散型和连续型。 离散型变量只能取有限个或可数个值，如骰子的点数； 连续型变量则可以取任何一个值，比如人的身高。 “概率分布”是概率论中的重要工具。它描述了随机变量可能取值的概率情况。 常见的概率分布包括伯努利分布、二项分布、正态分布等等。 正态分布，又被称为“钟形曲线”，在许多自然现象中都扮演着关键角色，比如人类的身高、体重等。 “贝叶斯定理”则允许我们根据新的证据更新对某个事件的信念。 换句话说，它告诉我们如何从先验知识中，结合新的观察结果，推算出更准确的概率估计。 掌握贝叶斯定理，如同掌握了一把钥匙，可以帮助我们更好地理解和处理不确定性。 “条件概率”是另一个重要的概念。 它描述了在已知某个事件已经发生的条件下，另一个事件发生的概率。 比如，已知某人是男性的条件下，他患某种疾病的概率，就属于条件概率的范畴。 总之，概率论不仅仅是数学的一个分支，更是一种思考方式，一种处理不确定性问题的能力。 希望这次复习能够帮助你更深入地理解概率论的精髓。
展开
概率论
2025-07-22
8次阅读