第 1 页 / 共 34 页
第 2 页 / 共 34 页
第 3 页 / 共 34 页
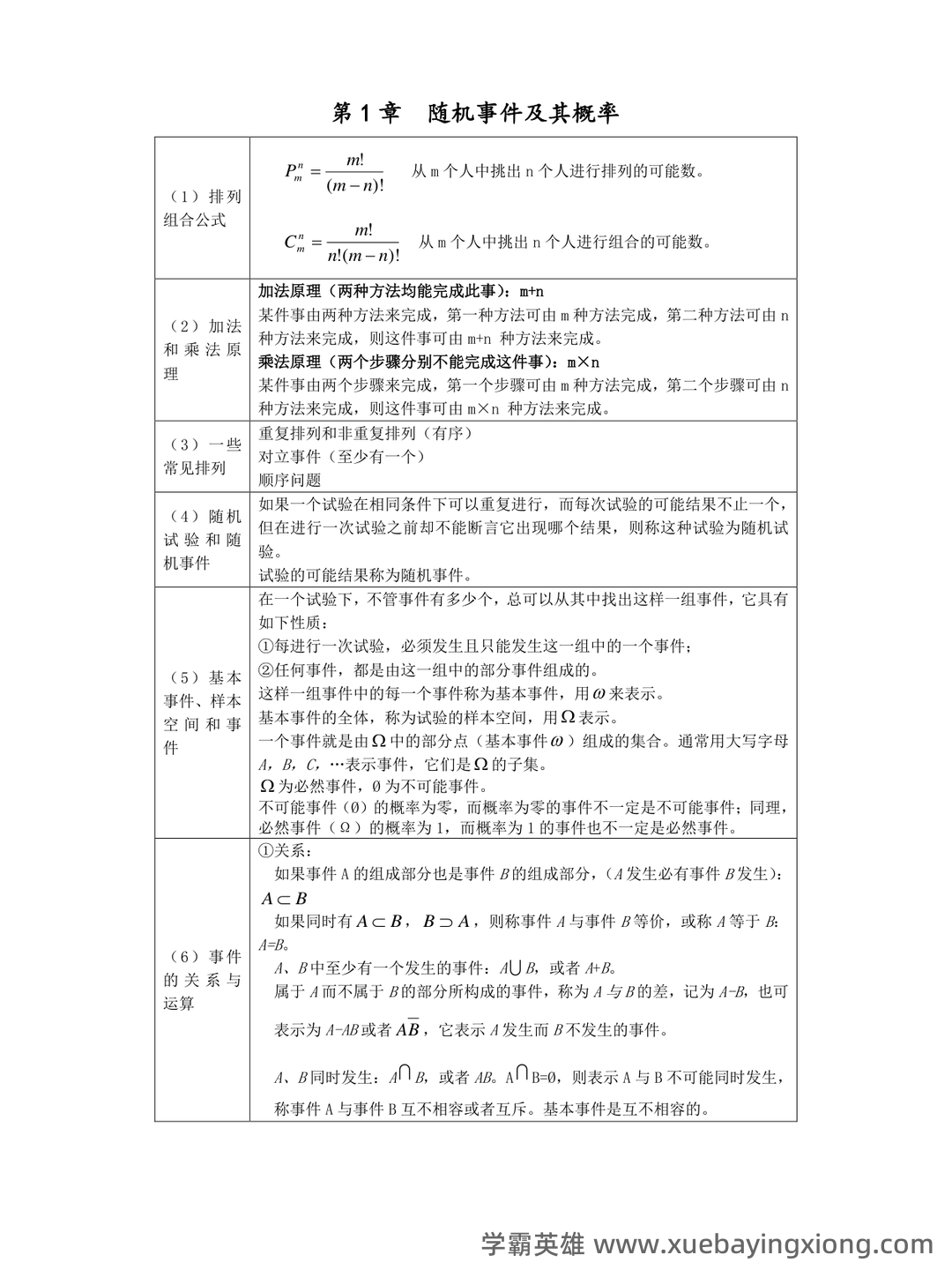
第 4 页 / 共 34 页
第 5 页 / 共 34 页
第 6 页 / 共 34 页
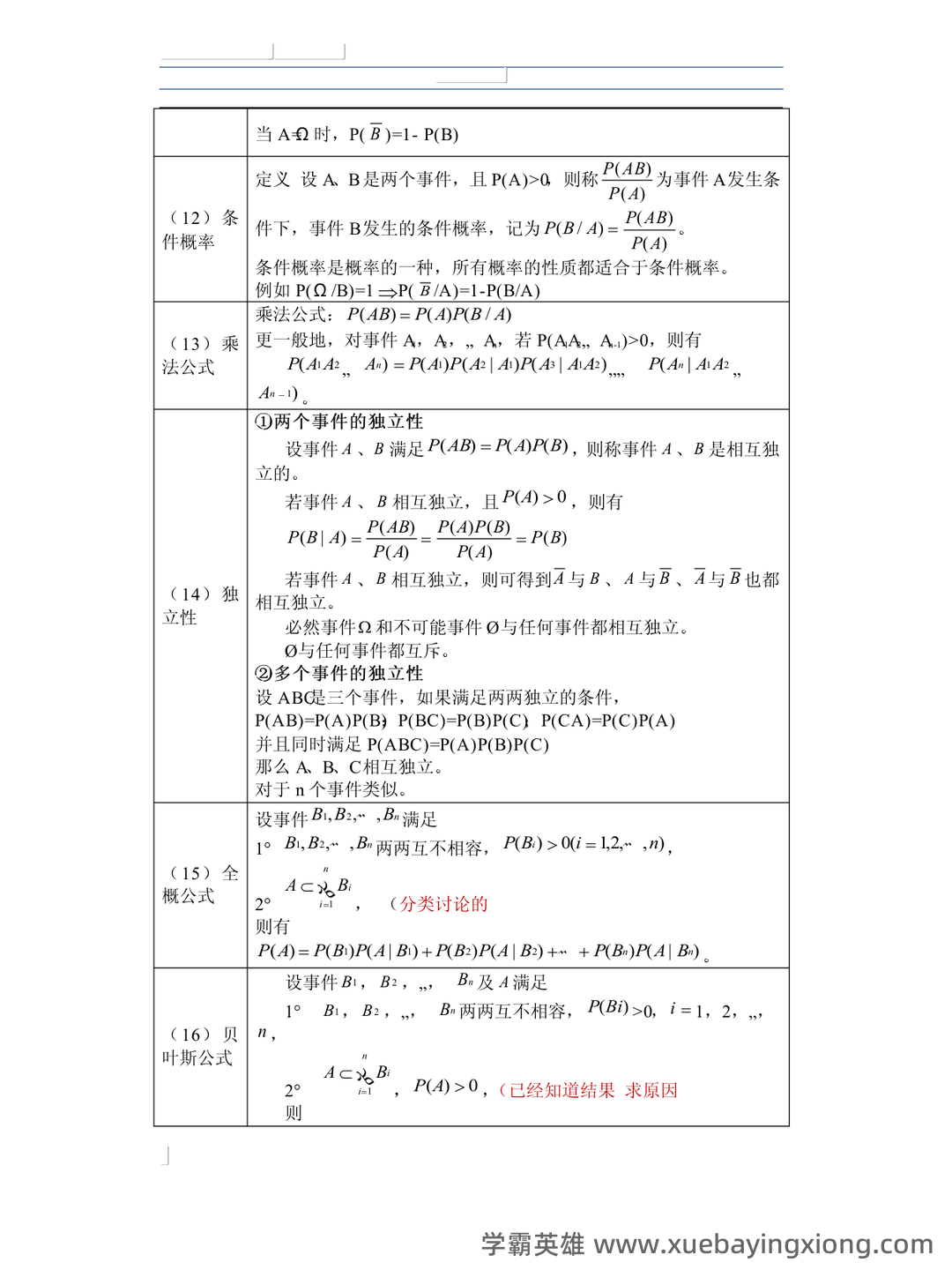
第 7 页 / 共 34 页
第 8 页 / 共 34 页
第 9 页 / 共 34 页
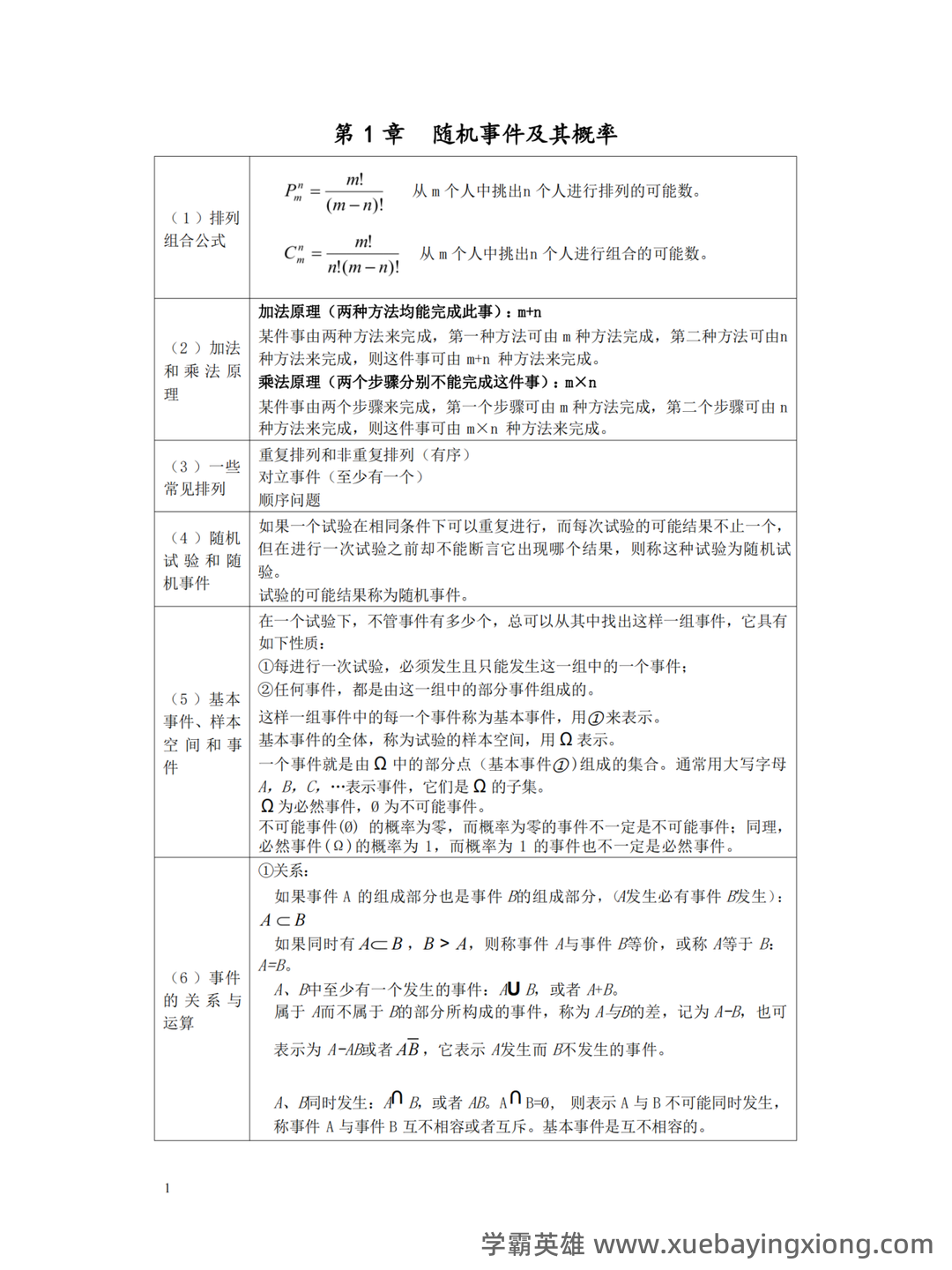
第 10 页 / 共 34 页
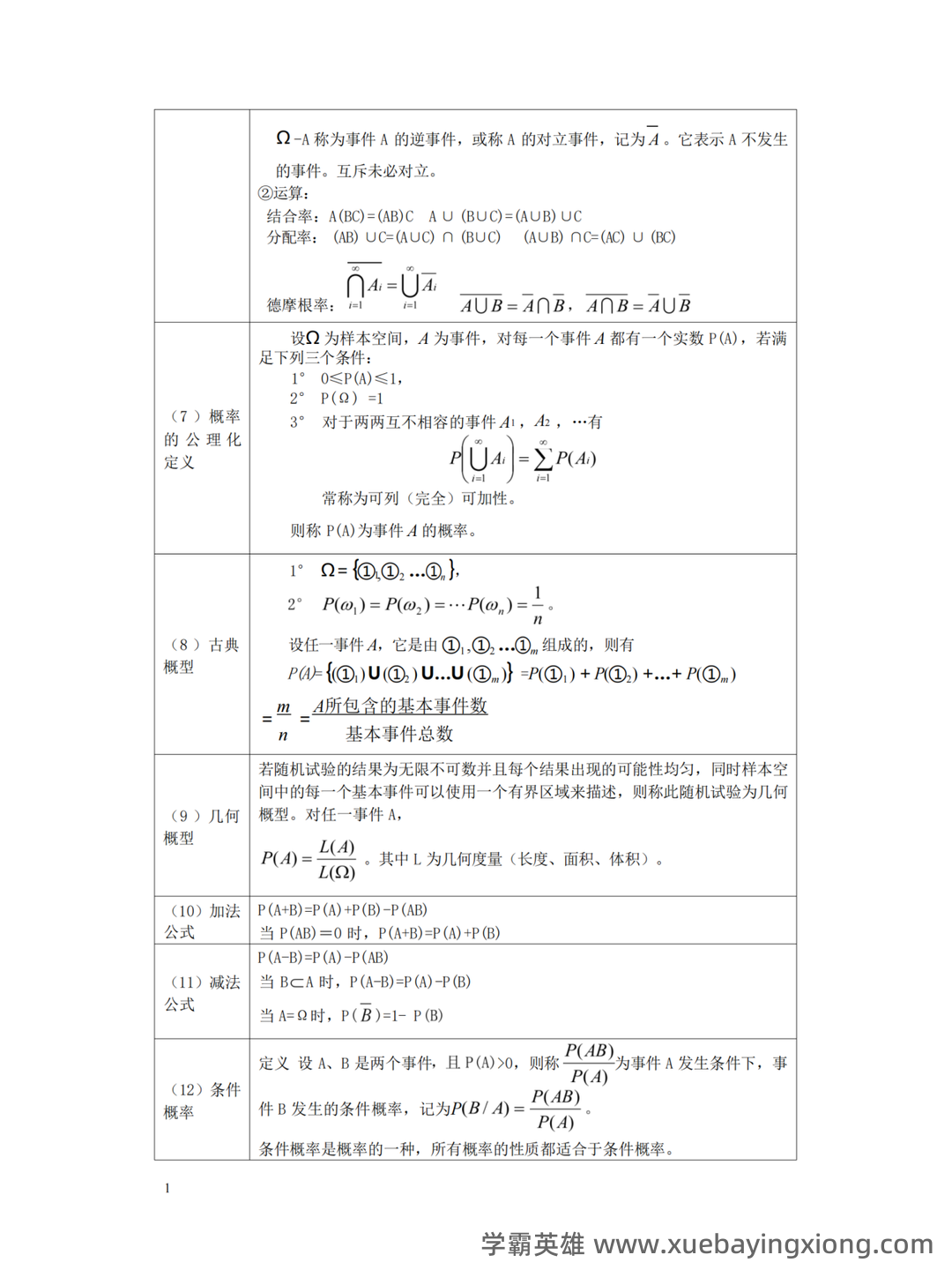
第 11 页 / 共 34 页
第 12 页 / 共 34 页
第 13 页 / 共 34 页
第 14 页 / 共 34 页
第 15 页 / 共 34 页
第 16 页 / 共 34 页
第 17 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (7)——Kolmogorov大数定律 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 18 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (7)——Kolmogorov大数定律 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 19 页 / 共 34 页
第 20 页 / 共 34 页
第 21 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (7)——Kolmogorov大数定律 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 22 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (7)——Kolmogorov大数定律 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 23 页 / 共 34 页
第 24 页 / 共 34 页
第 25 页 / 共 34 页
第 26 页 / 共 34 页
第 27 页 / 共 34 页
第 28 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (7)——Kolmogorov大数定律 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 29 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (7)——Kolmogorov大数定律 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 30 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (7)——Kolmogorov大数定律 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 31 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (7)——Kolmogorov大数定律 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 32 页 / 共 34 页
第 33 页 / 共 34 页
第 34 页 / 共 34 页
概率论复习笔记 (7)——Kolmogorov大数定律
概率论复习笔记 (7)——Kolmogorov大数定律 数学的世界总是充满着令人惊叹的规律，而Kolmogorov大数定律，无疑是概率论中最核心、也最迷人的定理之一。 简单来说，它告诉我们，当实验次数足够多时，随机变量的实际值会越来越接近其期望值。 这听起来似乎很直观，但其数学证明却充满了精妙。 在概率论中，我们经常会遇到“随机变量”的概念，例如抛硬币的结果（正面或反面）、掷骰子的点数等。这些都是随机变量，其值是不确定的，但我们可以通过统计的方法来估计其平均值，也就是期望值。 搜索词条“概率论”中，关于期望值的定义和计算方法都非常重要。 Kolmogorov大数定律的核心在于，这种“足够多”的次数，实际上并没有一个明确的数字上限。 随着实验次数的增加，随机变量的分布会越来越接近正态分布（如果满足正态分布假设），从而使得实际观测到的值与期望值之间的偏差越来越小。 这就像在扔硬币时，你扔了无数次，正面和反面的比例会越来越接近 50/50。 这个定律的应用非常广泛。 比如，在金融领域，我们可以利用大数定律来分析股票价格的波动，在医疗领域，可以利用大量患者的数据来评估某种疾病的发生率等等。 搜索词条“概率论”中，关于大数定律的理解，对于分析实际问题至关重要。 值得注意的是，大数定律并不能保证每次实验的结果都接近期望值，它只是在大量实验中，平均来看，结果会趋于稳定。 它强调的是统计规律的力量，告诉我们即使是随机事件，在足够大的样本量下，也能呈现出一定的规律性。 理解这个定律，是掌握概率论的关键一步。
展开
概率论
2025-07-22
9次阅读