第 1 页 / 共 34 页
第 2 页 / 共 34 页
第 3 页 / 共 34 页
第 4 页 / 共 34 页
第 5 页 / 共 34 页
第 6 页 / 共 34 页
第 7 页 / 共 34 页
第 8 页 / 共 34 页
第 9 页 / 共 34 页
第 10 页 / 共 34 页
第 11 页 / 共 34 页
第 12 页 / 共 34 页
第 13 页 / 共 34 页
第 14 页 / 共 34 页
第 15 页 / 共 34 页
第 16 页 / 共 34 页
第 17 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (4)——概率的公理化定义延伸 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 18 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (4)——概率的公理化定义延伸 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 19 页 / 共 34 页
第 20 页 / 共 34 页
第 21 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (4)——概率的公理化定义延伸 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 22 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (4)——概率的公理化定义延伸 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 23 页 / 共 34 页
第 24 页 / 共 34 页
第 25 页 / 共 34 页
第 26 页 / 共 34 页
第 27 页 / 共 34 页
第 28 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (4)——概率的公理化定义延伸 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 29 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (4)——概率的公理化定义延伸 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 30 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (4)——概率的公理化定义延伸 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 31 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论复习笔记 (4)——概率的公理化定义延伸 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 32 页 / 共 34 页
第 33 页 / 共 34 页
第 34 页 / 共 34 页
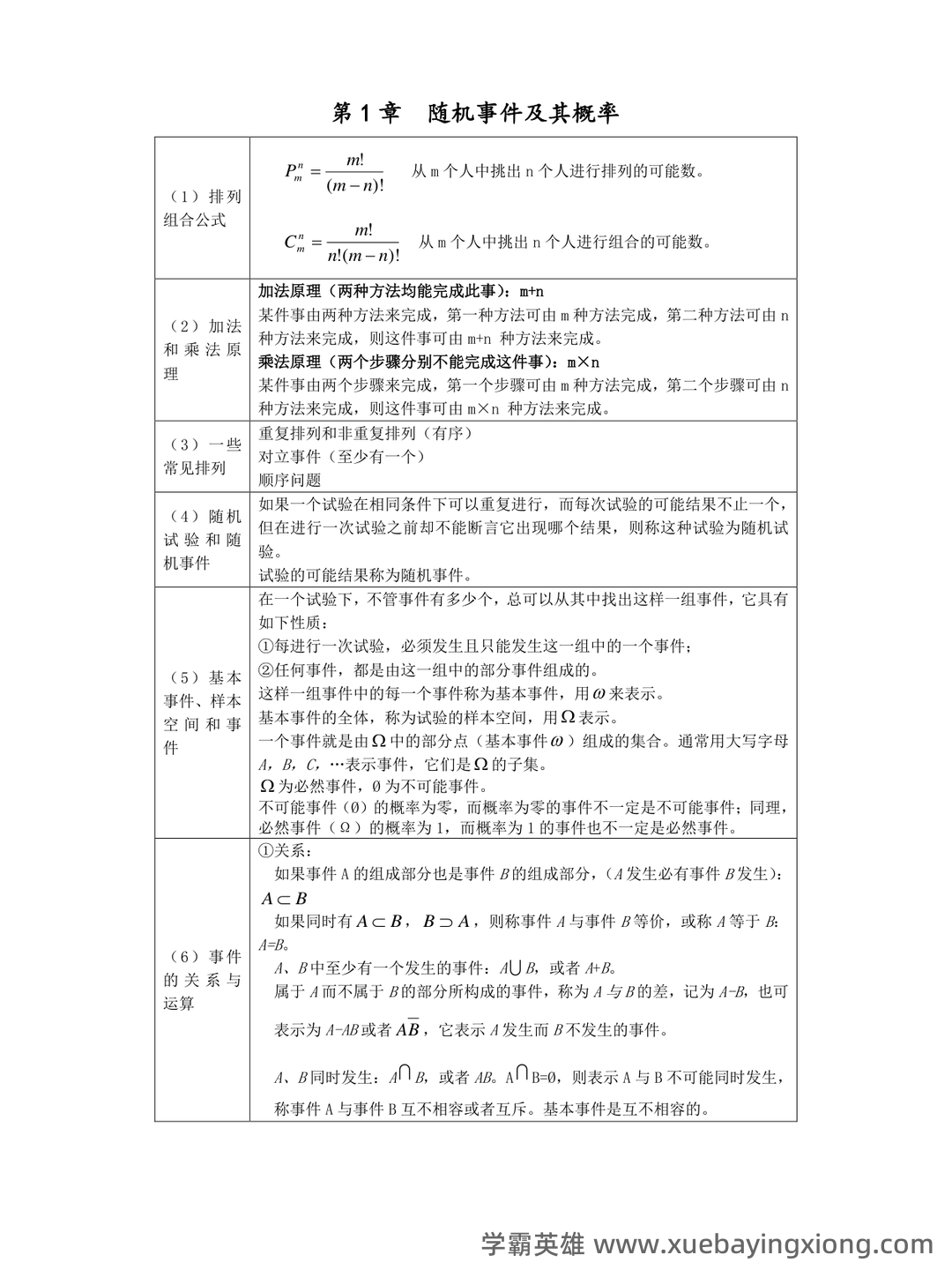
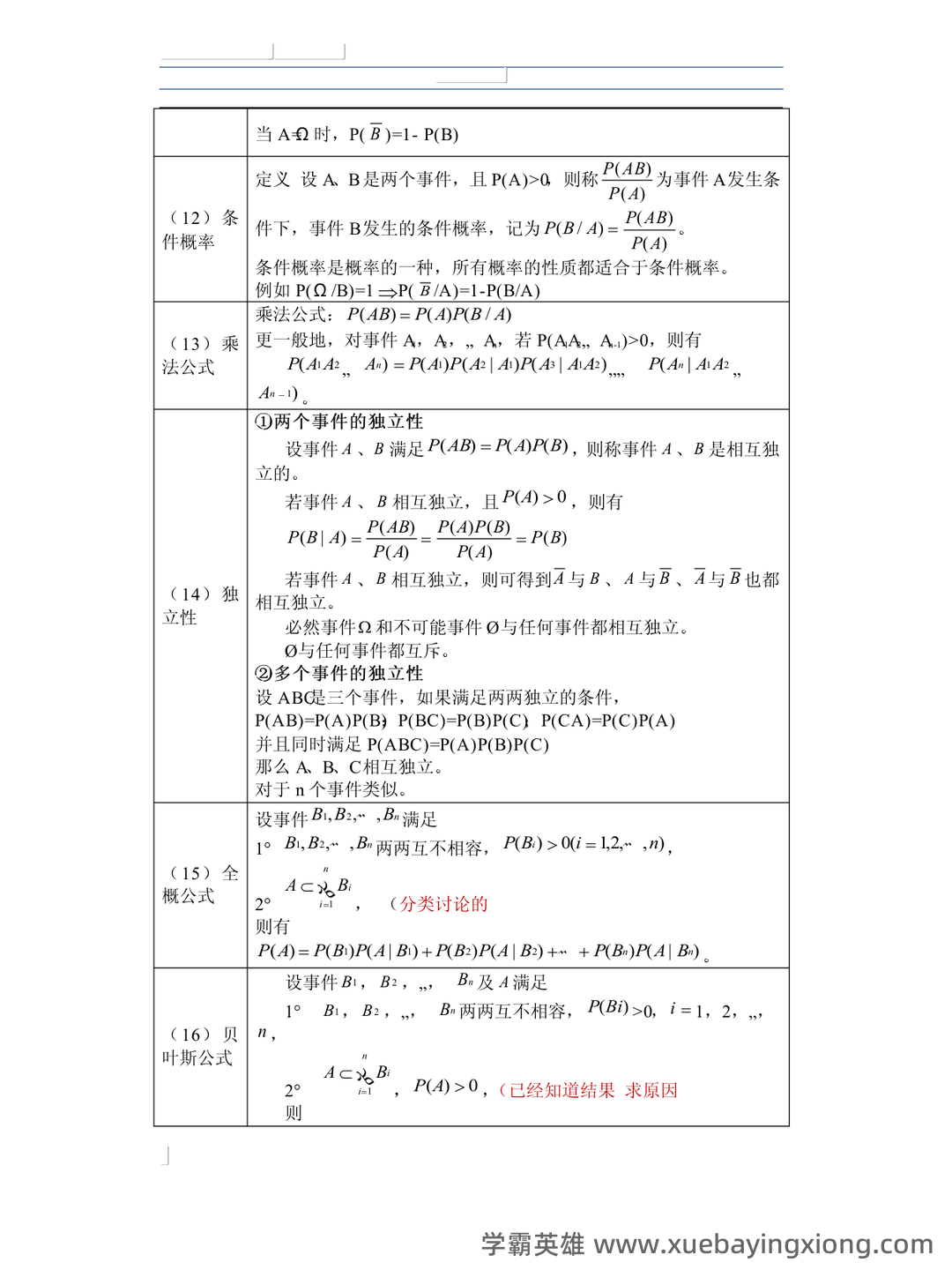
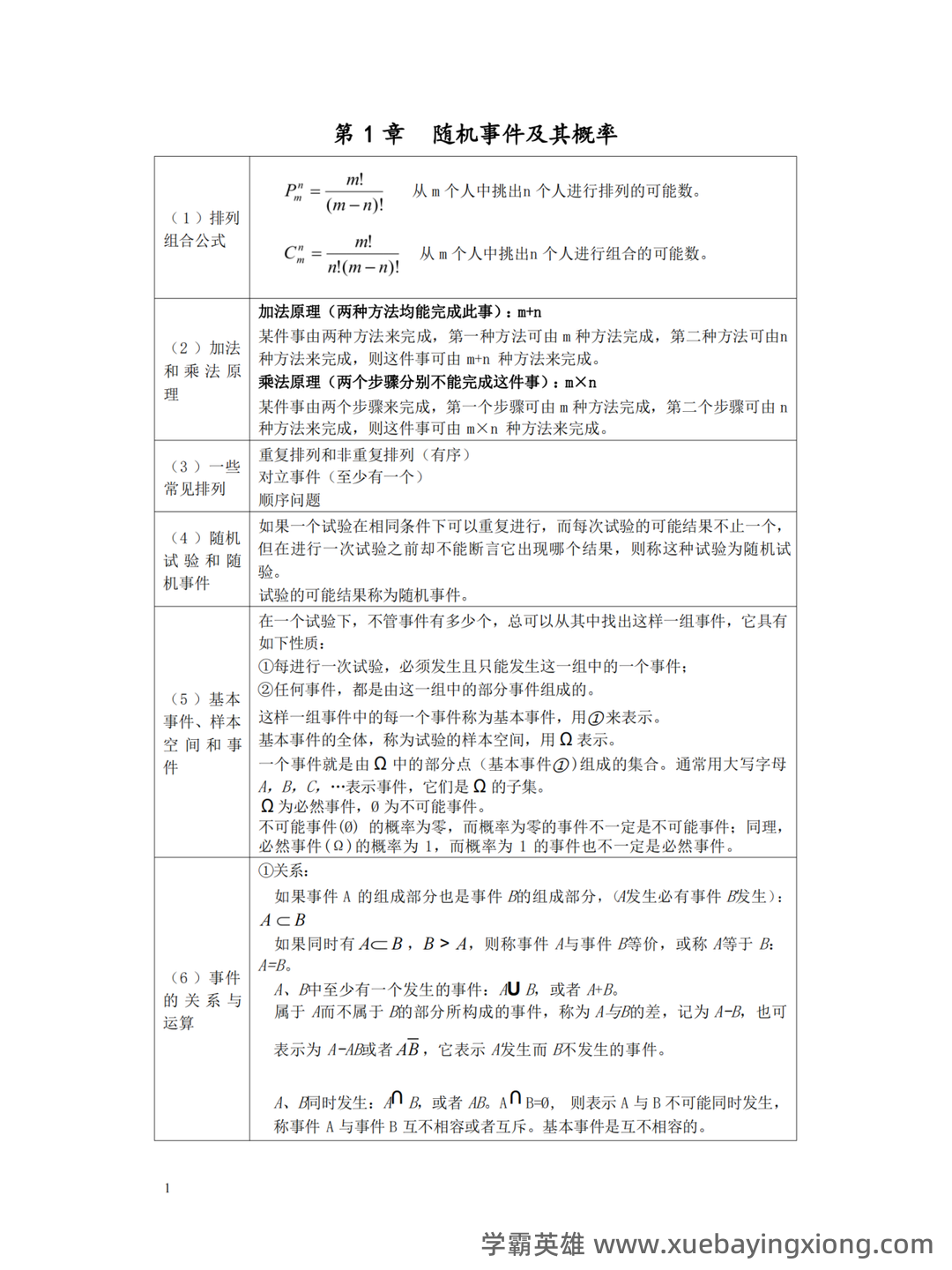
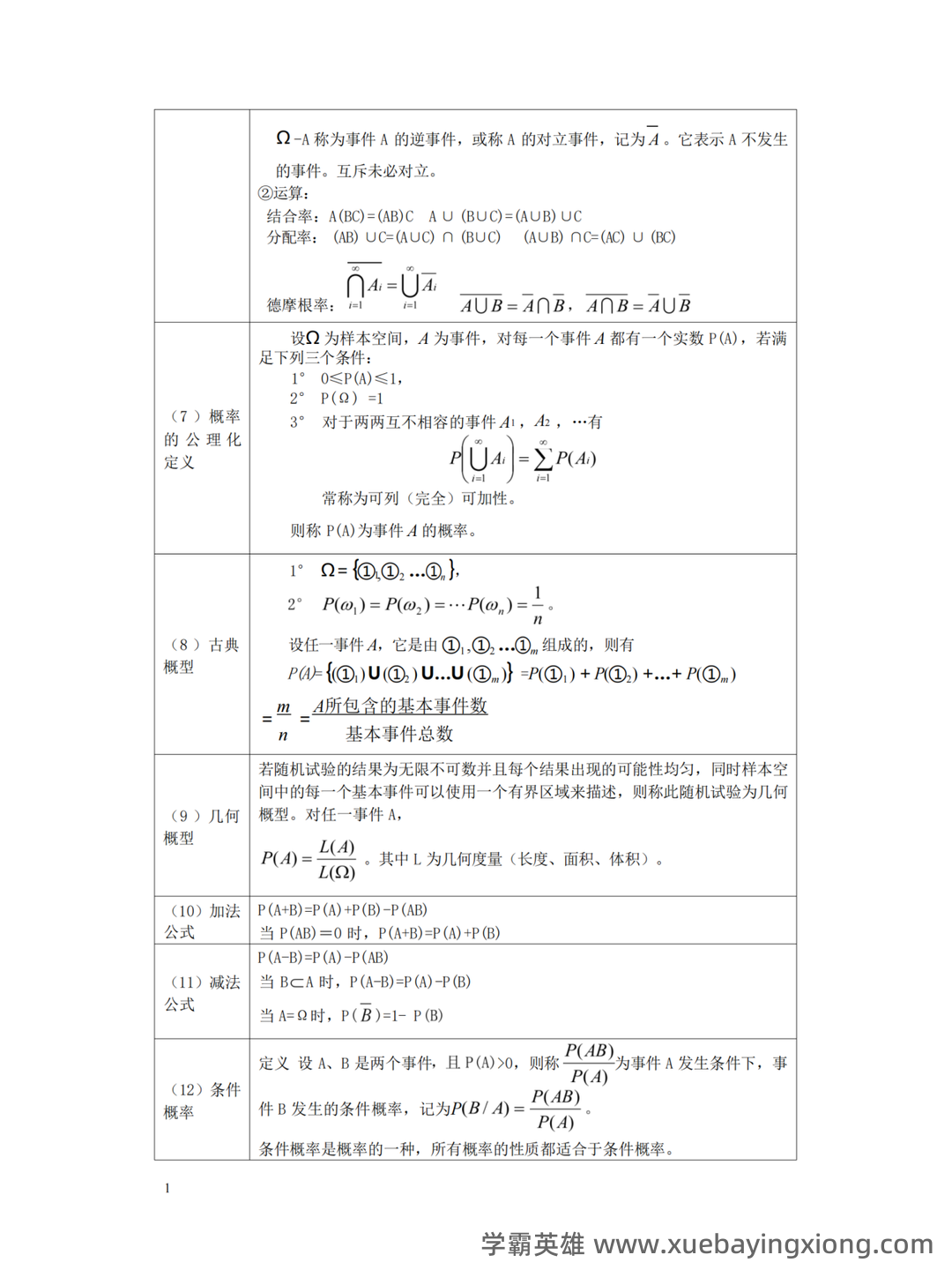
概率论复习笔记 (4)——概率的公理化定义延伸
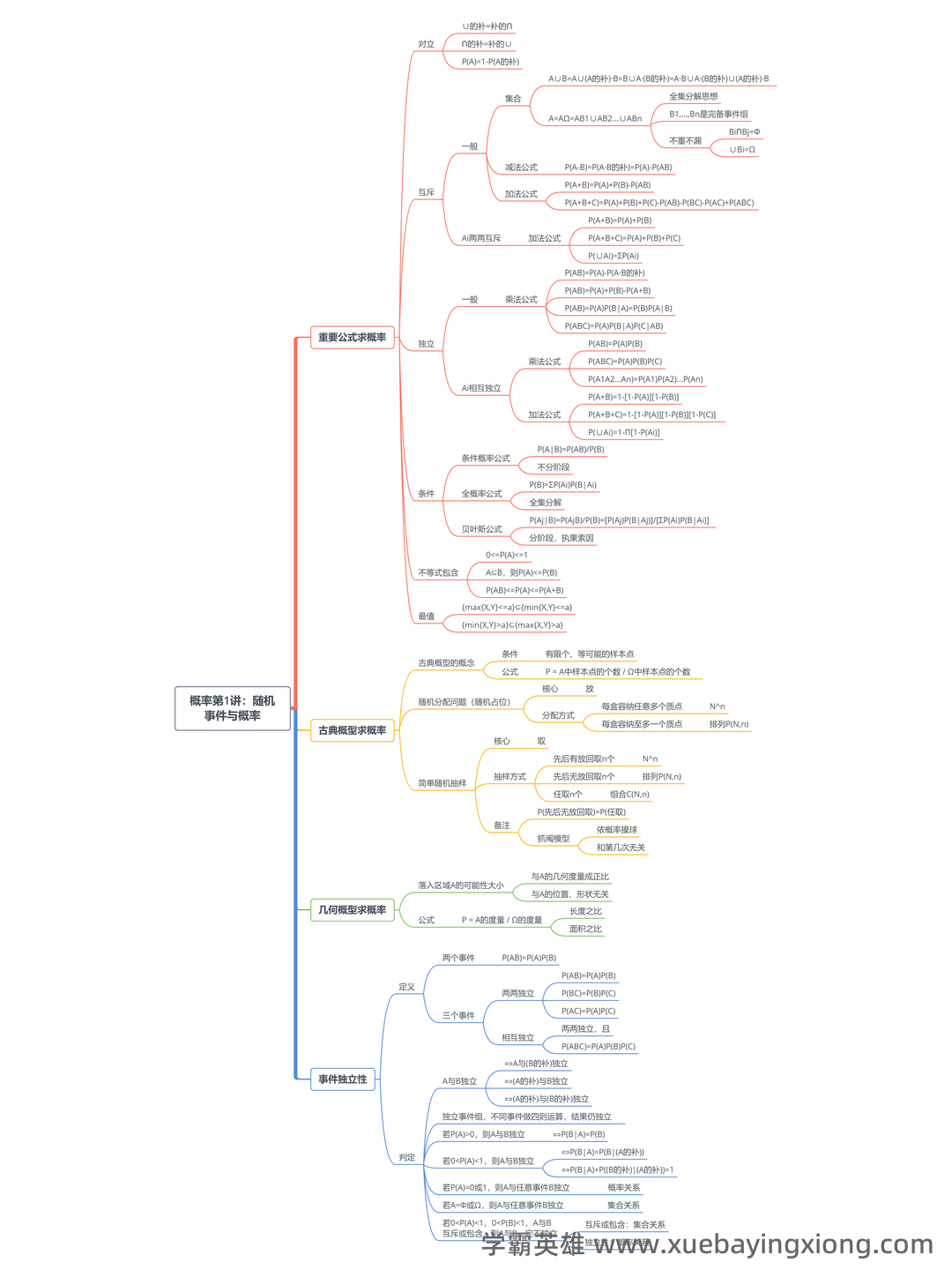
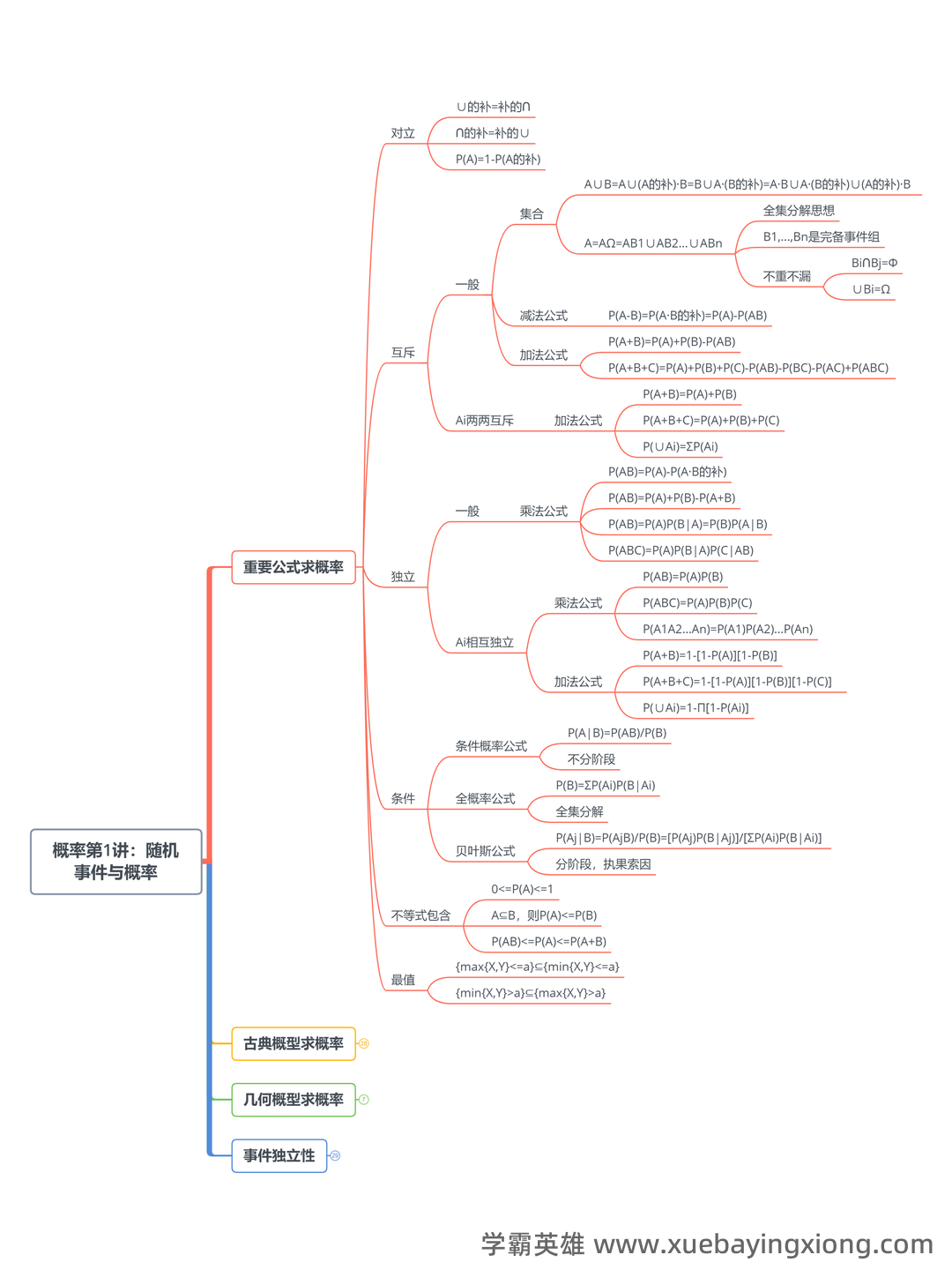
概率论复习笔记 (4)——概率的公理化定义延伸 概率论，这门看似抽象的学科，其实在根基上建立在几个核心公理之上。之前的笔记我们回顾了“样本空间”、“事件”、“概率”的基本概念，这些都是概率论构建逻辑框架的基石。但仅仅定义这些概念还远远不够，真正的突破在于对概率的更深层理解——公理化定义。 按照经典概率论的定义，一个随机实验的结果是完全随机的，意味着所有可能的结果都具有相同的概率。也就是说，对于一个事件A，P(A) = n/N，其中n是事件A中成功的次数，N是实验所有可能结果的总数。这个定义简洁明了，但同时也隐含了“均一分布”的假设，即每个结果发生的概率相等。这有点像说，抛硬币，每一面朝上的概率都是1/2，这在现实中可能并非总是如此。 然而，这种公理化的定义在很多情况下都非常实用，尤其是在解决各种随机现象时。例如，在模拟掷骰子，我们可以假设骰子的每个面都有相同的概率，然后通过大量的模拟来估计期望值。 这种方法虽然简化了问题，但仍然依赖于概率的公理化定义作为基础。 值得注意的是，现代概率论也存在其他形式的定义，比如频率学派的定义，它认为概率是长期实验中事件发生频率的极限。 但无论采用哪种定义， 概率的公理化基础始终是概率论的起点，也是我们理解和应用概率论的根本。
展开
概率论
2025-07-22
7次阅读