第 1 页 / 共 34 页
第 2 页 / 共 34 页
第 3 页 / 共 34 页
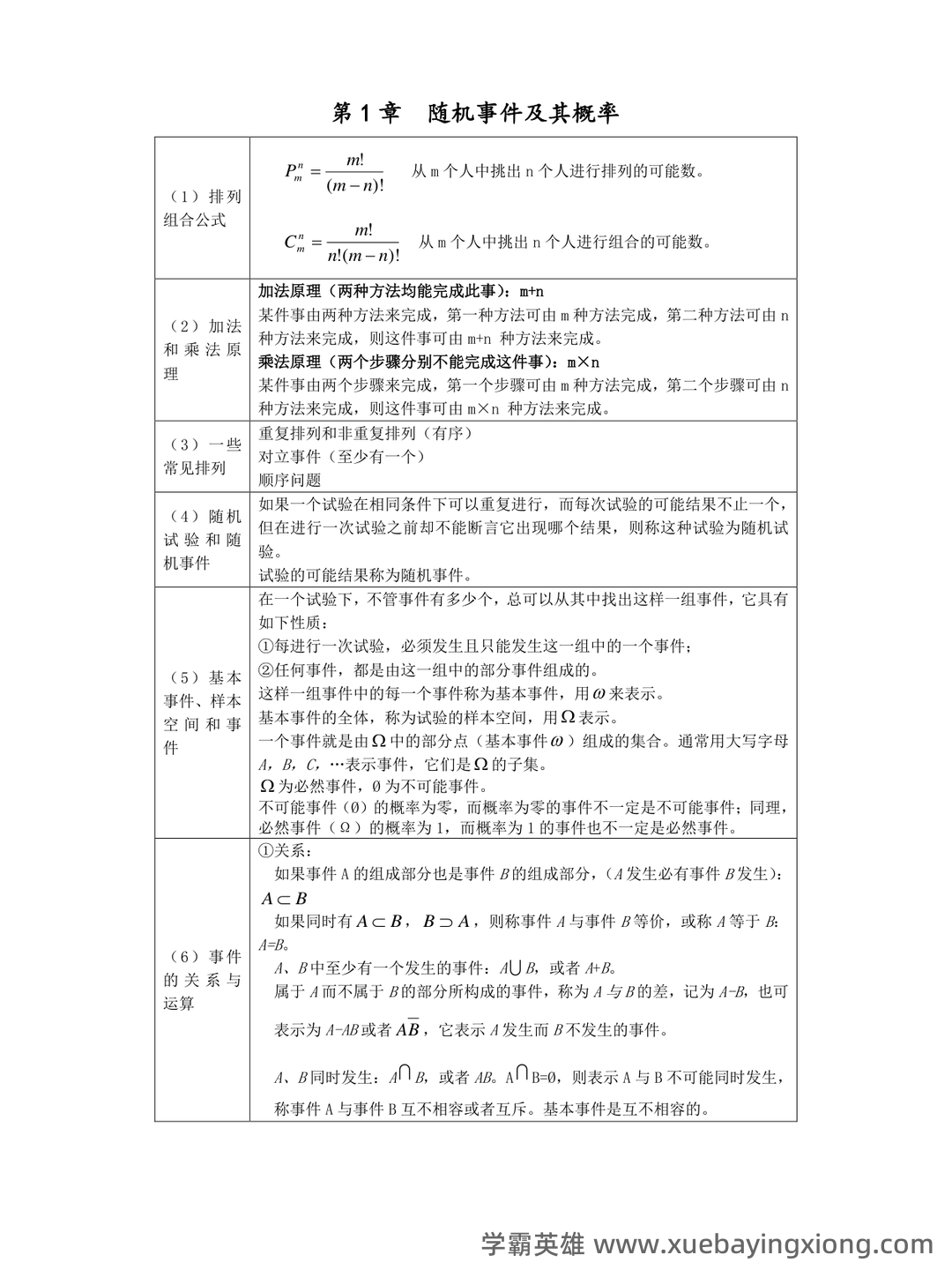
第 4 页 / 共 34 页
第 5 页 / 共 34 页
第 6 页 / 共 34 页
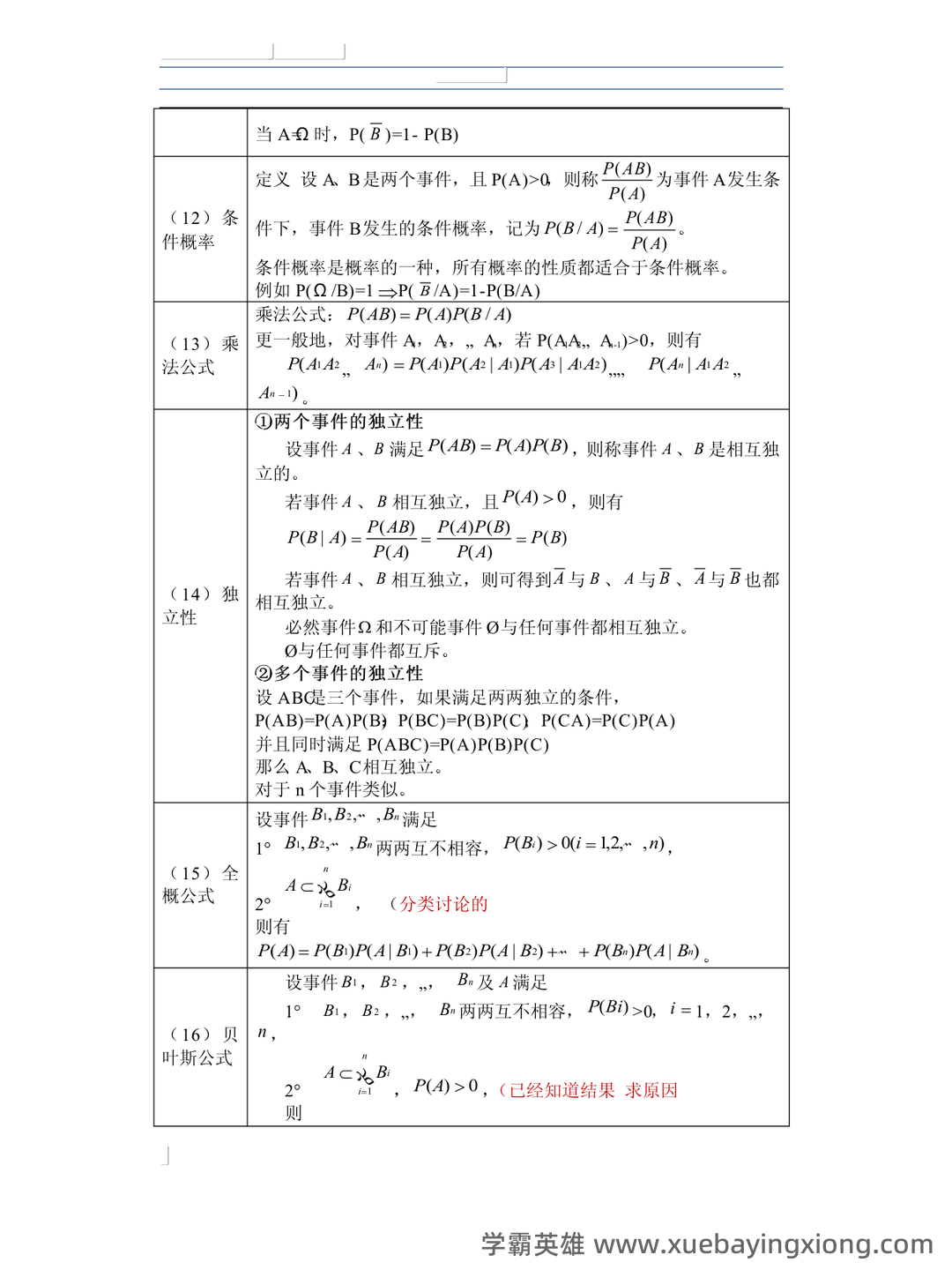
第 7 页 / 共 34 页
第 8 页 / 共 34 页
第 9 页 / 共 34 页
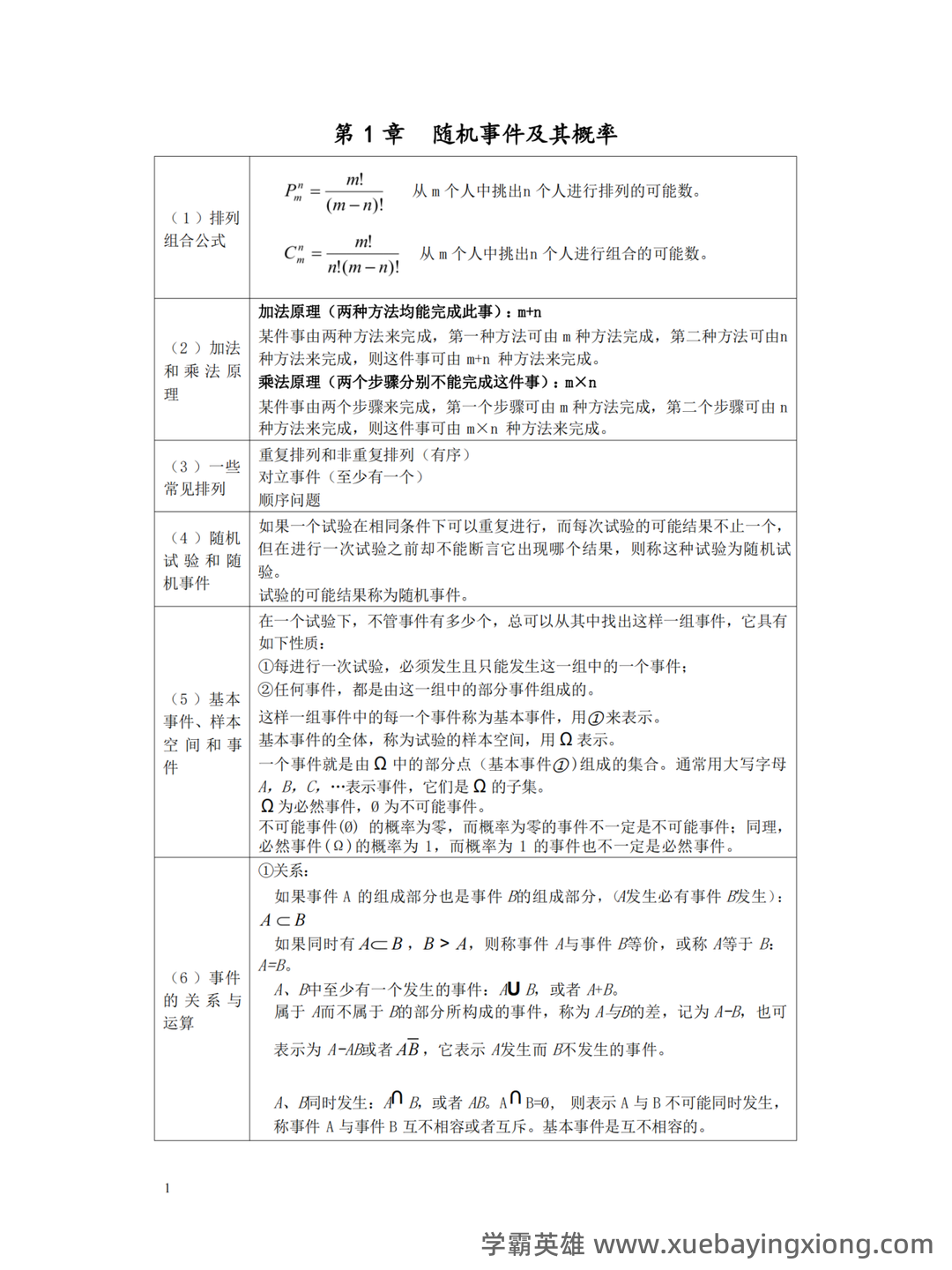
第 10 页 / 共 34 页
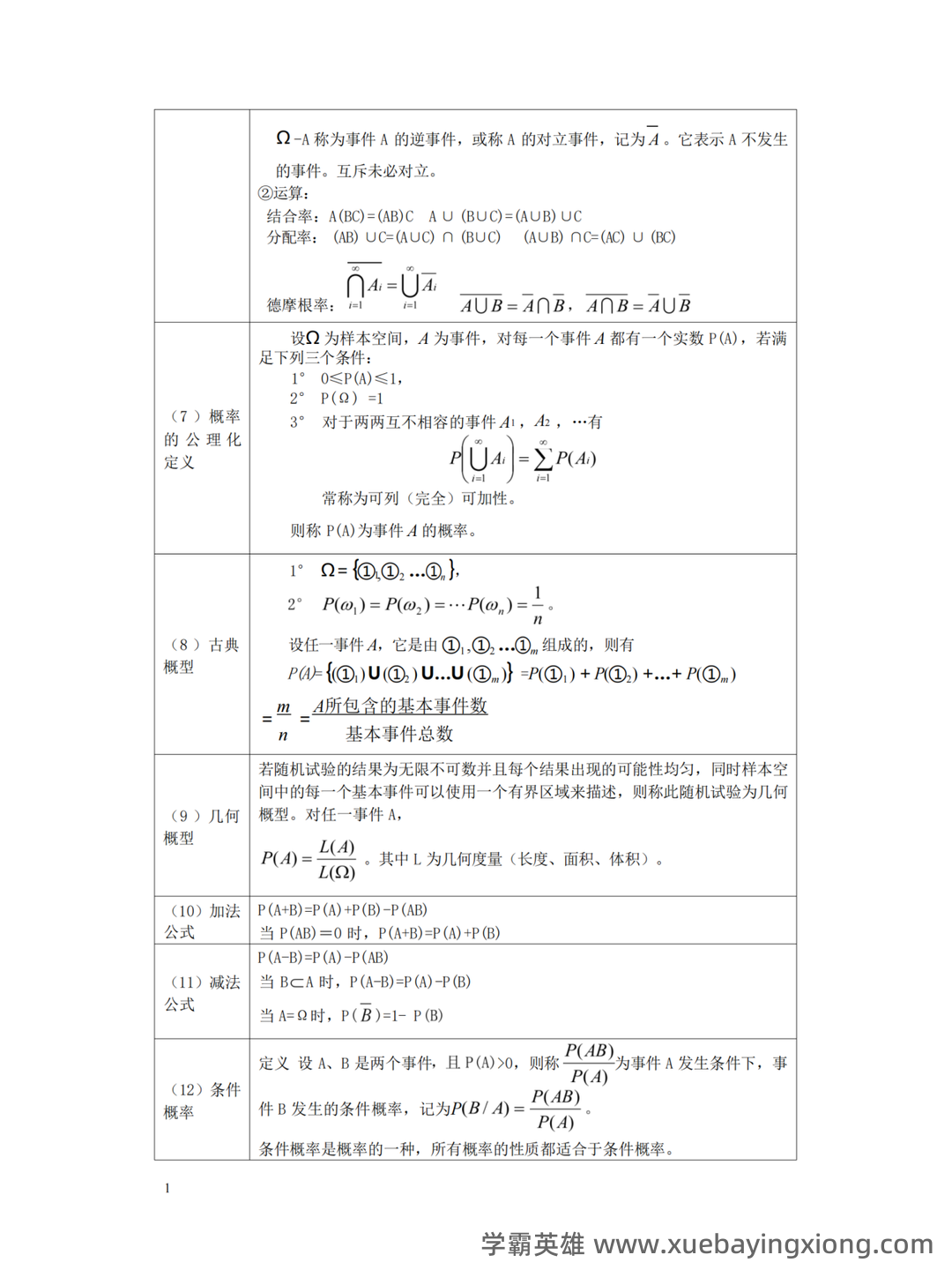
第 11 页 / 共 34 页
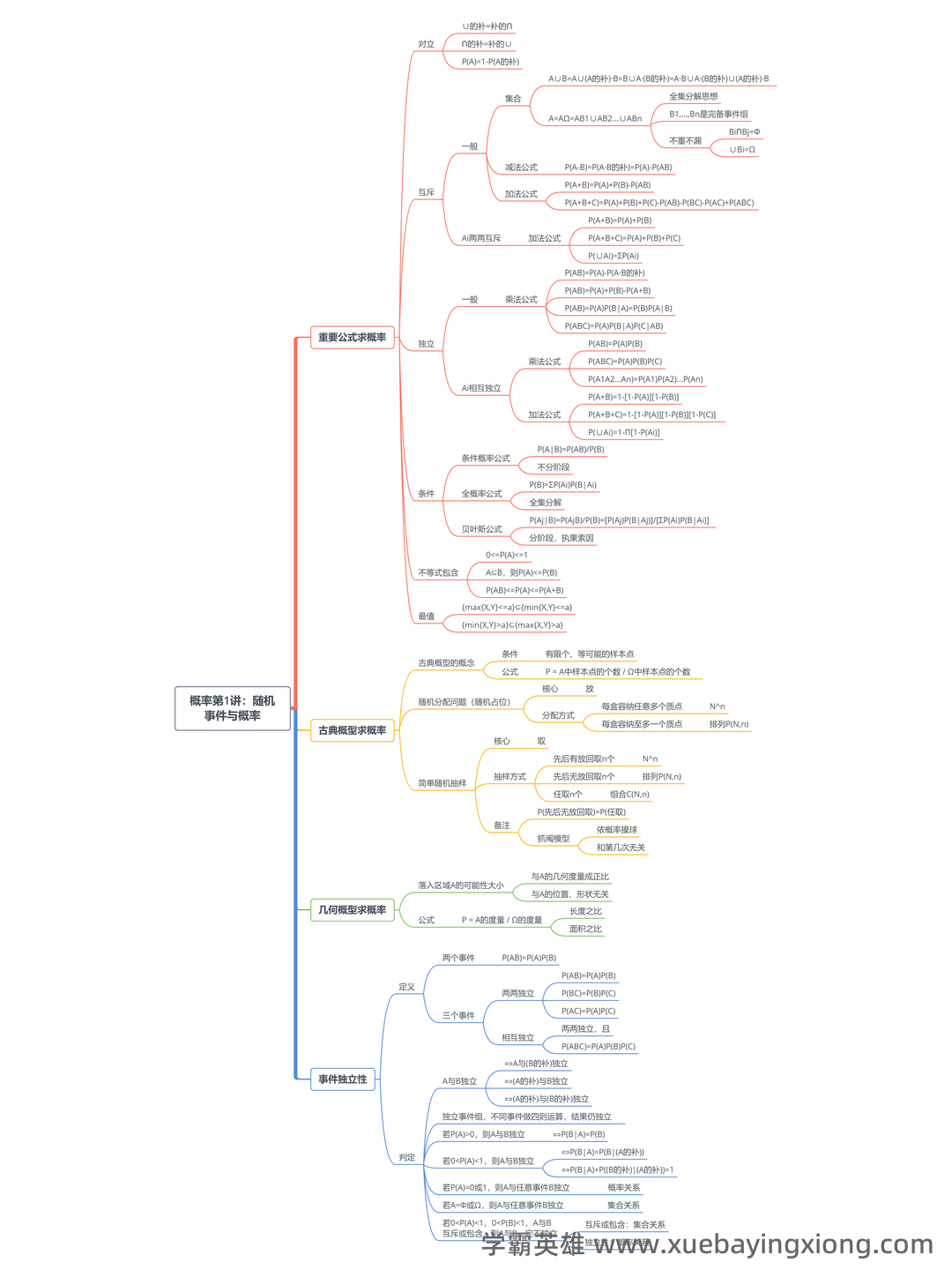
第 12 页 / 共 34 页
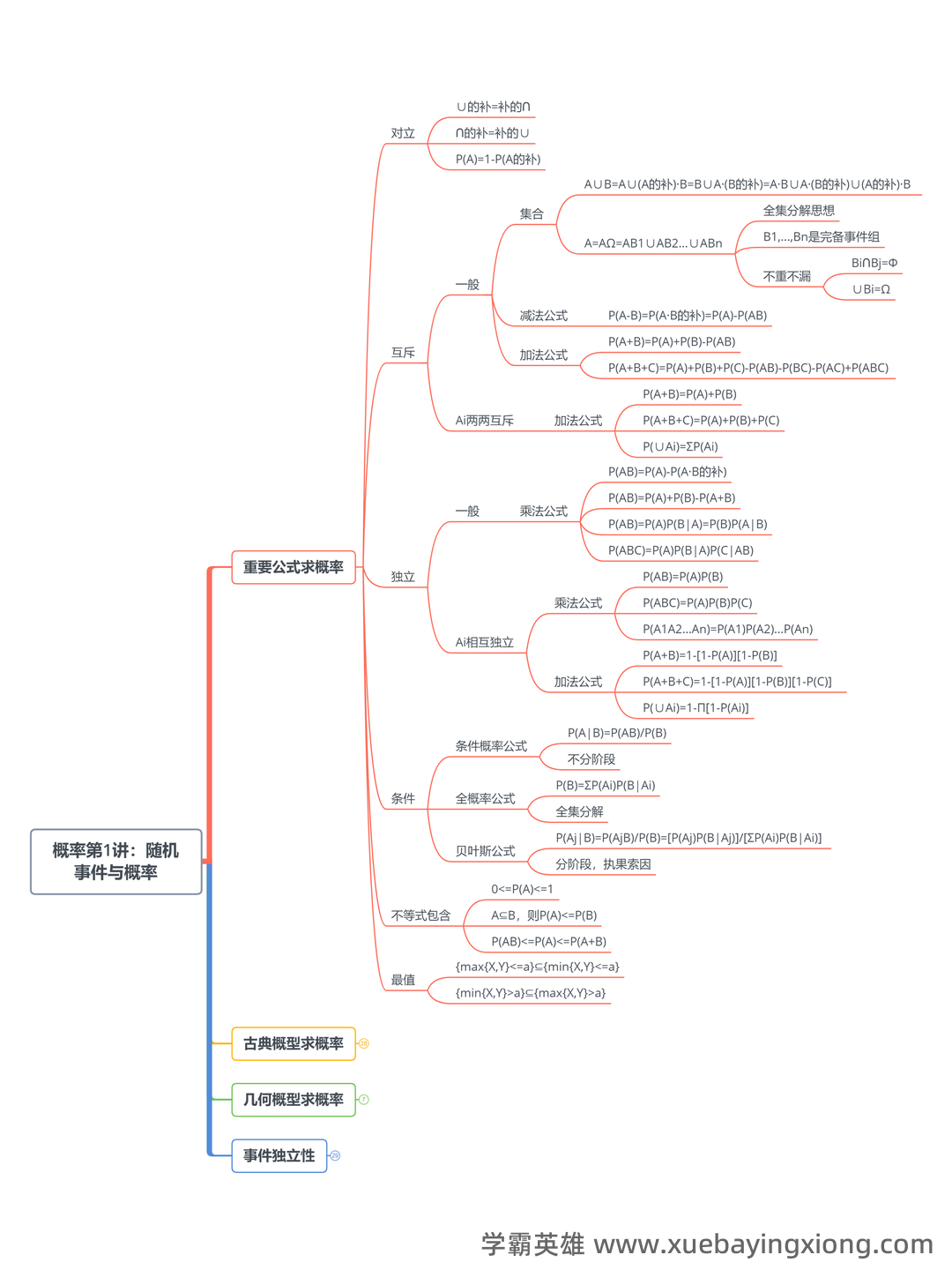
第 13 页 / 共 34 页
第 14 页 / 共 34 页
第 15 页 / 共 34 页
第 16 页 / 共 34 页
第 17 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】期末不挂科复习笔记_已知fx(x)求fy(y) - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 18 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】期末不挂科复习笔记_已知fx(x)求fy(y) - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 19 页 / 共 34 页
第 20 页 / 共 34 页
第 21 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】期末不挂科复习笔记_已知fx(x)求fy(y) - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 22 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】期末不挂科复习笔记_已知fx(x)求fy(y) - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 23 页 / 共 34 页
第 24 页 / 共 34 页
第 25 页 / 共 34 页
第 26 页 / 共 34 页
第 27 页 / 共 34 页
第 28 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】期末不挂科复习笔记_已知fx(x)求fy(y) - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 29 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】期末不挂科复习笔记_已知fx(x)求fy(y) - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 30 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】期末不挂科复习笔记_已知fx(x)求fy(y) - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 31 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】期末不挂科复习笔记_已知fx(x)求fy(y) - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 32 页 / 共 34 页
第 33 页 / 共 34 页
第 34 页 / 共 34 页
【概率论与数理统计】期末不挂科复习笔记_已知fx(x)求fy(y)
【概率论与数理统计】期末不挂科复习笔记_已知fx(x)求fy(y) 概率论，简直就是统计学的心脏。掌握它，就像学会了读懂世界运行的规律。特别是要记住，概率论的核心在于建立数学模型，用数学语言描述和分析随机现象。 这次复习，咱们重点突破已知fx(x)求fy(y)这个常见问题。 首先，概率论的基础是联合概率分布。 假设我们已知随机变量X和Y的联合概率密度函数 fx(x) 和 fy(y)。 解决这个问题，关键在于利用条件概率的定义。 记住，条件概率的公式是：P(A|B) = P(A∩B) / P(B)， 换句话说，P(A|B) 表示在已知B发生的条件下，A发生的概率。 接下来，求 fy(y) 的关键在于理解 fx(x) 和 fy(y) 之间的关系。 很多时候，我们需要知道 fx(x) 是关于 X 的，而 fy(y) 是关于 Y 的。所以，要想求 fy(y)，我们常常需要将 fx(x) 转化为关于 y 的形式。 具体步骤通常是：将 fx(x) 表示为 y 关于 x 的函数，例如 y = g(x)。 然后，利用条件概率公式，结合 fy(y) 的定义，就可以得到 fy(y) 的表达式。 这需要一定的逻辑思维和代数运算能力。 别忘了，在计算过程中，务必检查所有变量的单位是否一致，确保结果的合理性。 解决这类问题，多做一些练习，熟能生巧！ 相信通过这次复习，你一定能轻松应对期末考试，不再为期末成绩发愁！
展开
概率论
2025-07-22
7次阅读