《概率论与数理统计》知识点总结(详细).pdf
《概率论与数理统计》复习提纲.pdf
《概率论与数理统计》练+答案.pdf
《概率论与数理统计》思维导图.pdf
《概率论与数理统计》公式整理.pdf
《概率论与数理统计》知识点(详细).pdf
《概率论与数理统计》复习资料.pdf
《概率论与数理统计》练(含答案).pdf
《概率论与数理统计》复习串讲笔记.pdf
《概率论与数理统计》知识点总结（超详细）.pdf
《概率论与数理统计》期末考试题.pdf
《概率论与数理统计》知识点总结.pdf
《概率论与数理统计》公式.pdf
《概率论与数理统计》笔记.pdf
《概率论与数理统计》知识点.pdf
《概率论与数理统计》练(附答案).pdf
《概率论与数理统计》提纲.pdf
第 1 页 / 共 1 页
概率论期末复习资料：思维导图+复习重点梳理
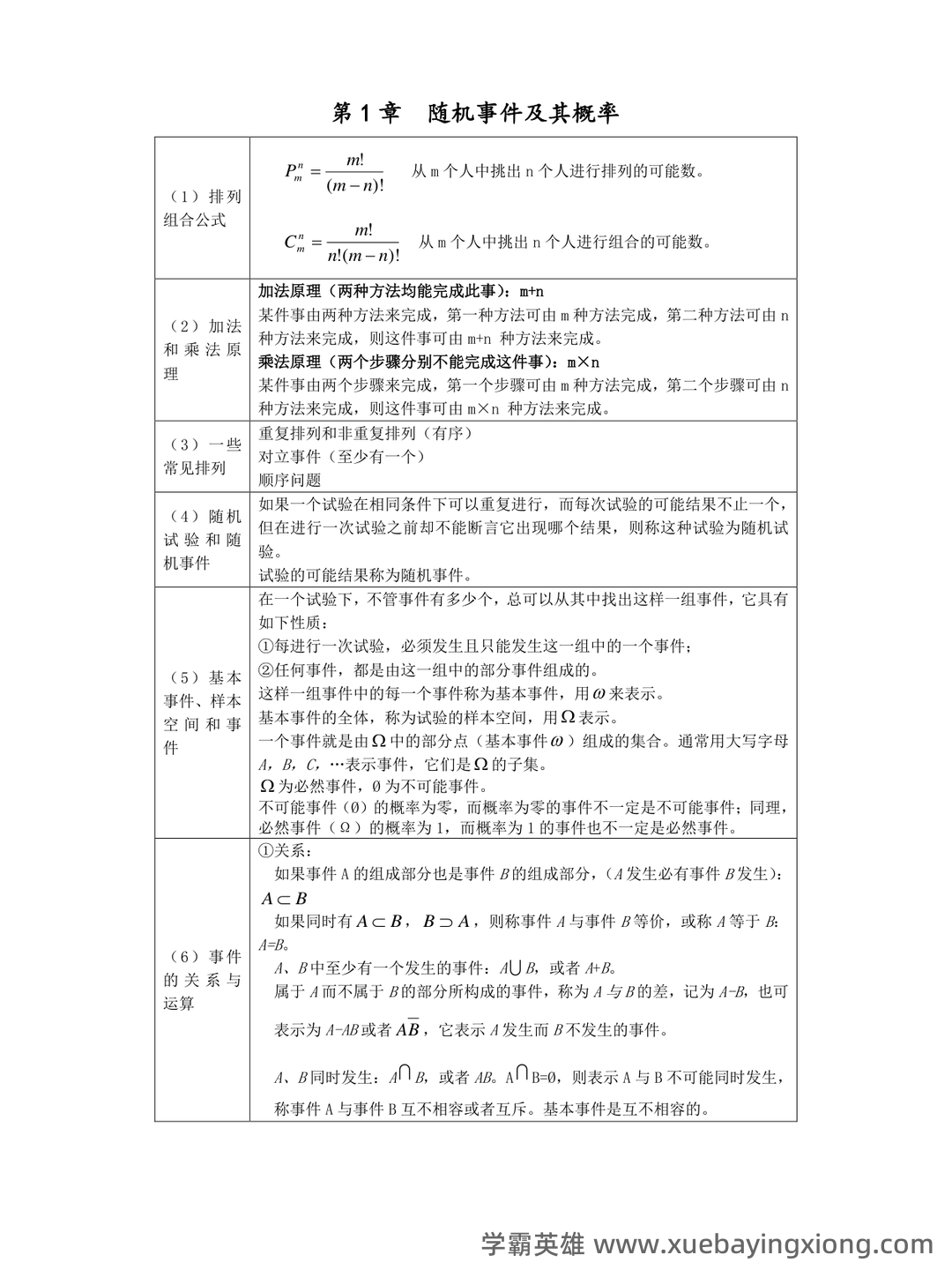
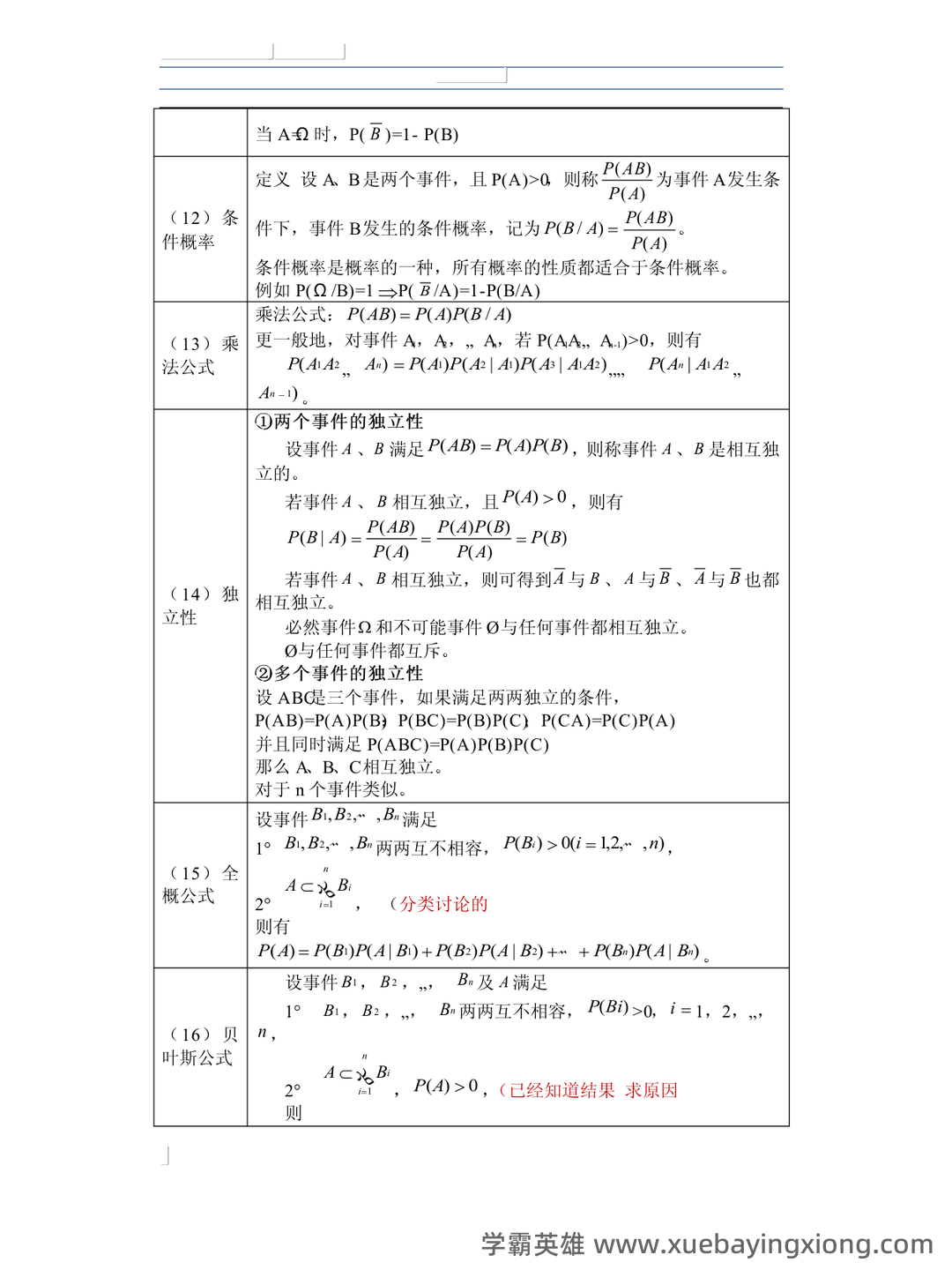
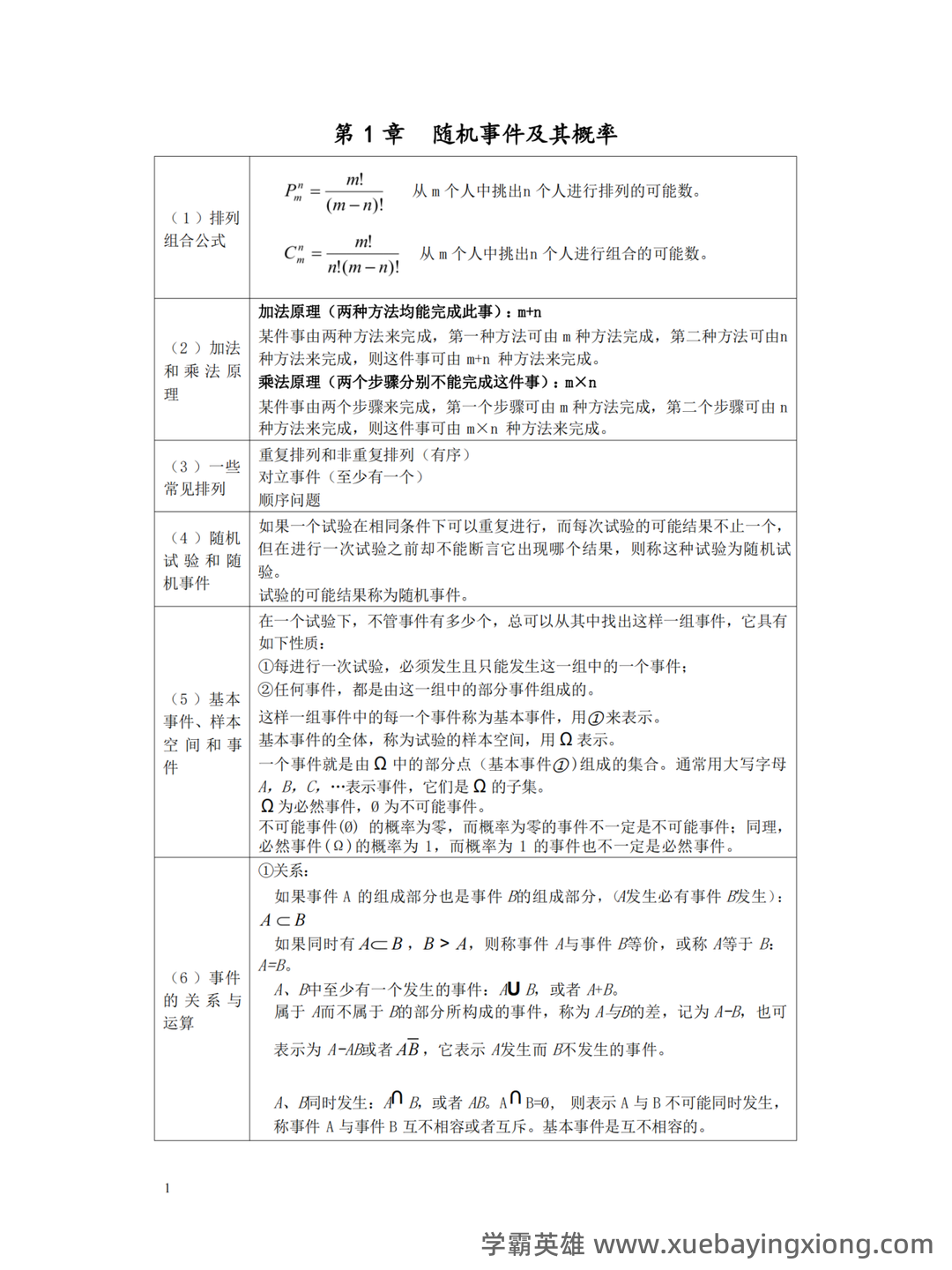
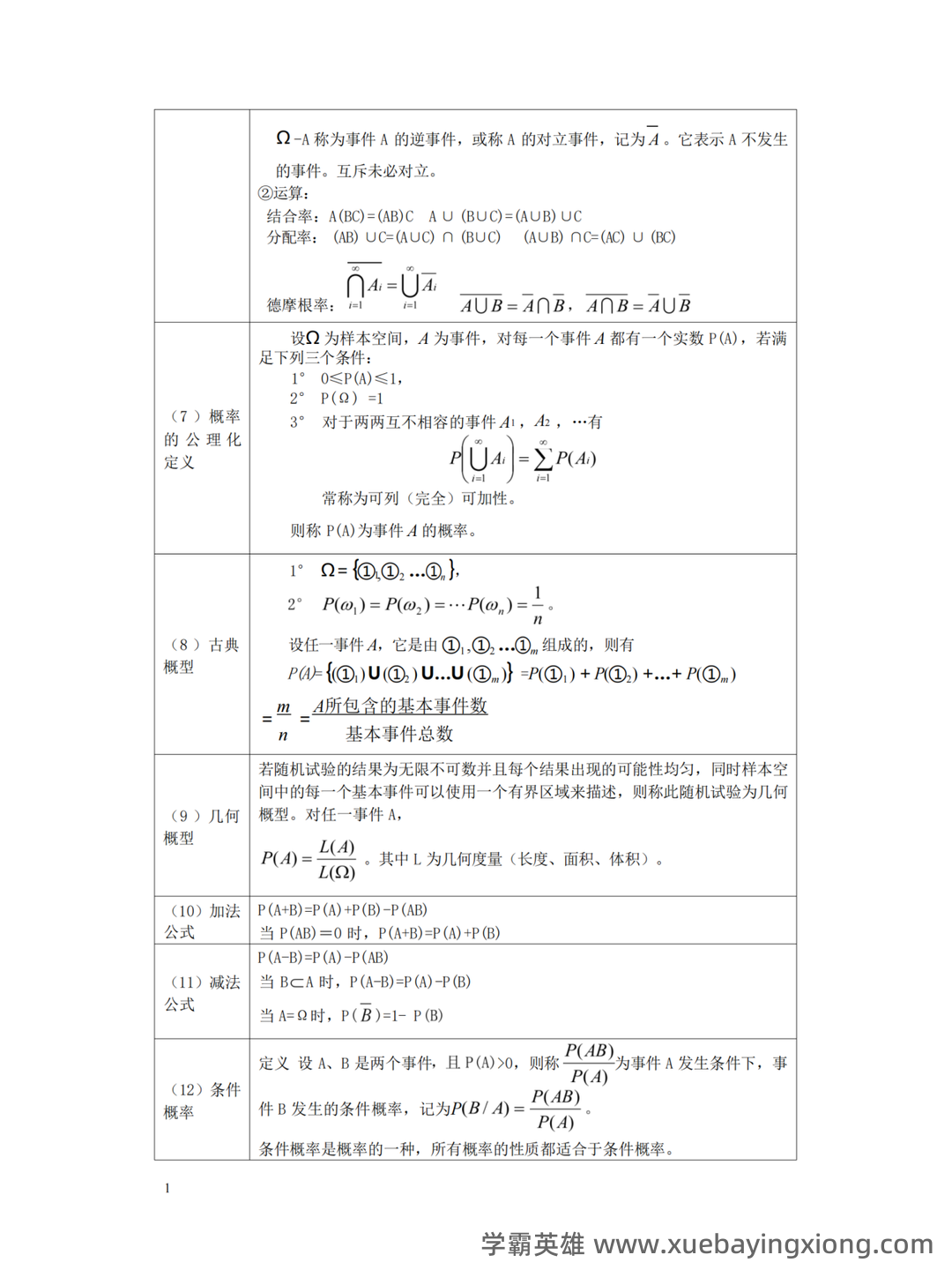
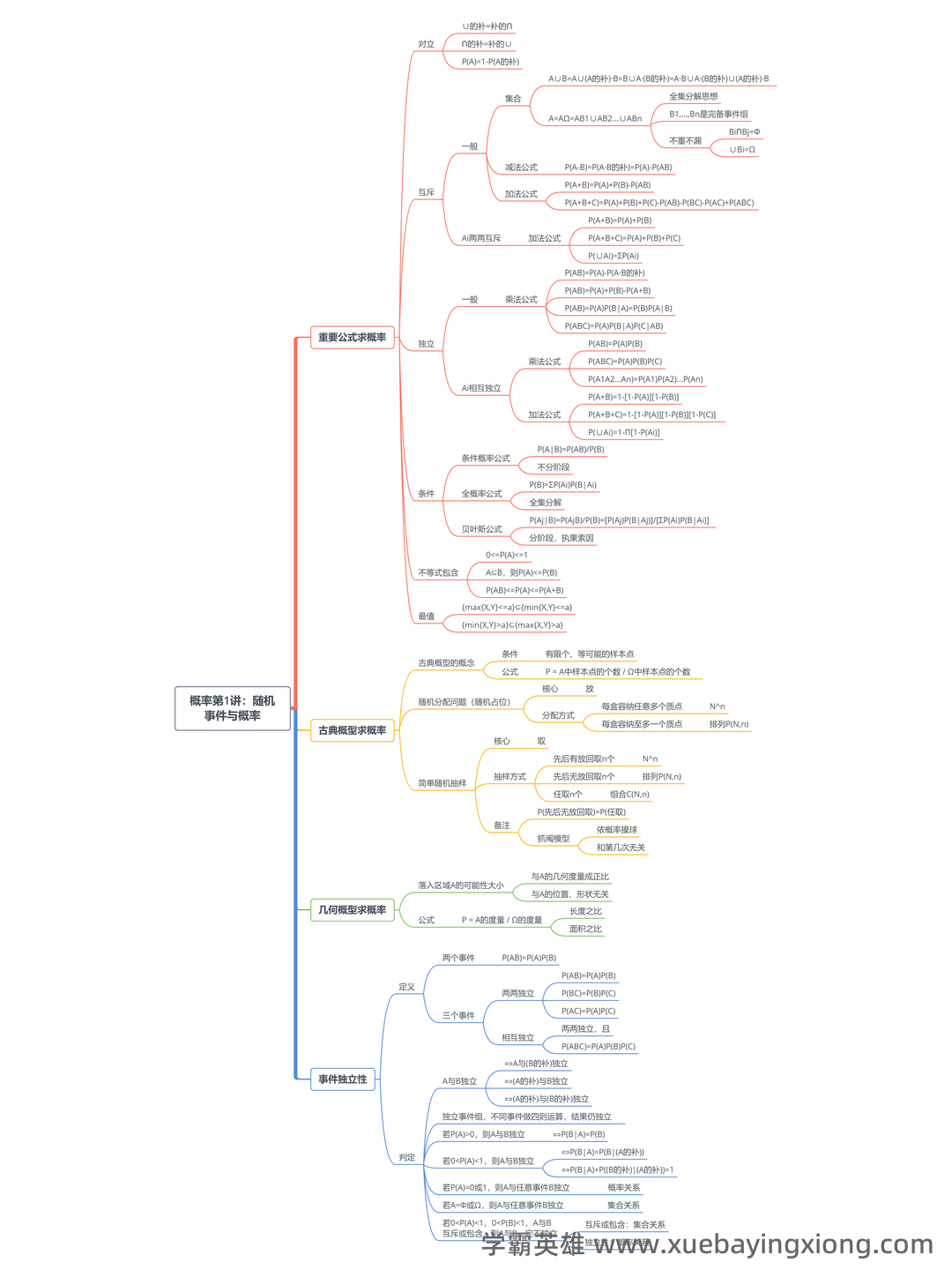
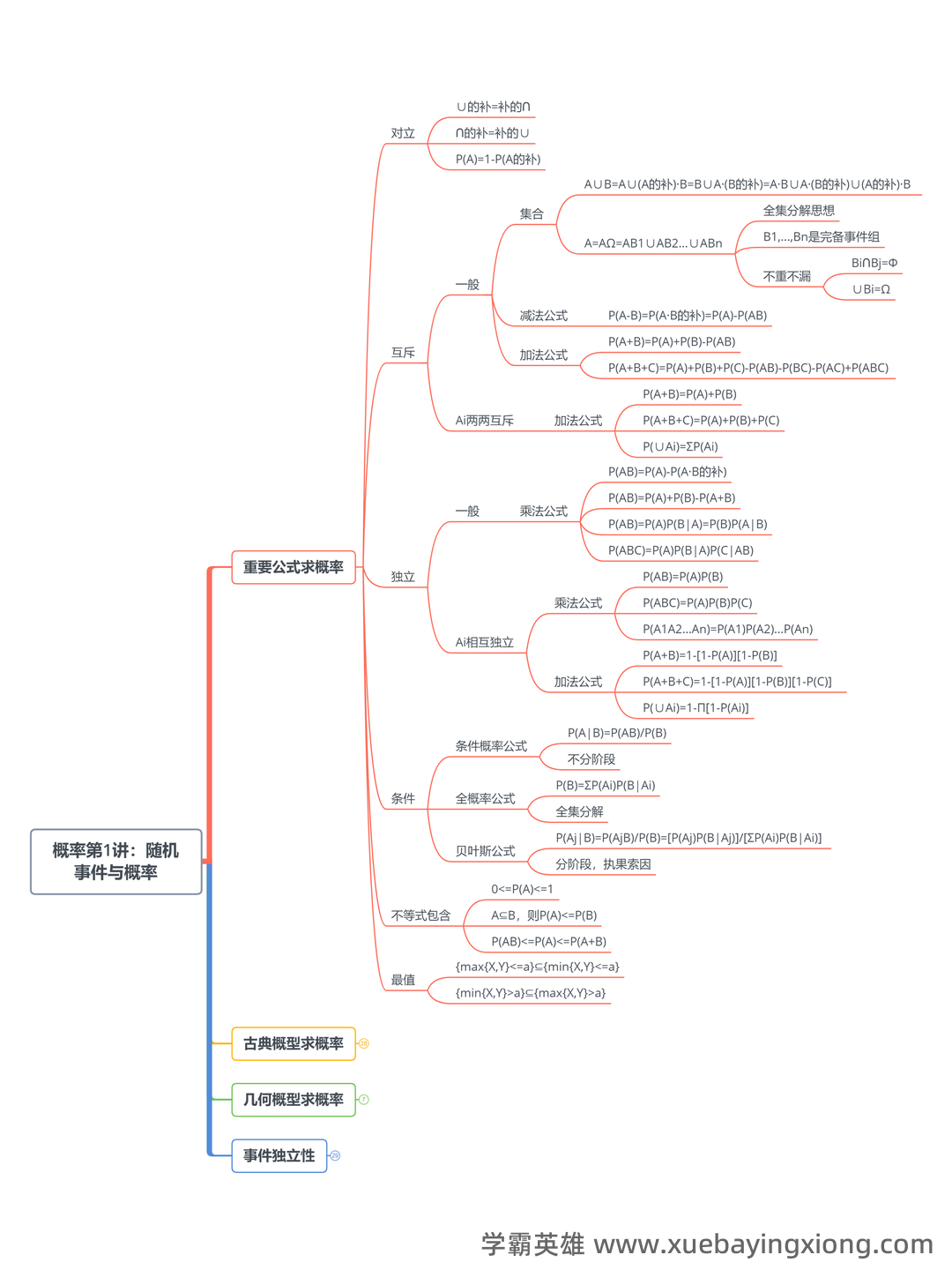
概率论期末复习资料：思维导图+复习重点梳理 准备期末概率论考试，时间紧迫？掌握好概率论核心概念，提升应试信心，这份期末复习资料能帮你事半功倍。我们将以思维导图的形式，结合关键复习重点，构建一个高效的学习框架。 一、思维导图构建 首先，我们将概率论的主要内容概括为以下几个核心节点： 概率基础: 包括概率的定义、概率事件、样本空间、古典概率、频率概率等。 条件概率: 核心概念是“条件概率公式”P(A|B) = P(A∩B) / P(B)，理解其与全概率公式的联系至关重要。 贝叶斯定理: 作为条件概率的延伸，贝叶斯定理提供了一个更新概率的途径，公式为：P(A|B) = [P(B|A)P(A)] / P(B)。 随机变量: 区分离散型和连续型随机变量，理解其概率分布（如二项分布、正态分布等）。 期望、方差、协方差: 概率论中的重要量，理解它们在分析随机变量中的作用。 二、复习重点梳理 1. 概率定义理解: 概率是衡量事件发生的可能性大小的量，不同类型的概率（如古典概率、频率概率）的区别和联系。 2. 条件概率的应用: 多做条件概率相关的例题，熟练掌握条件概率公式的应用场景。 3. 贝叶斯定理的意义: 理解贝叶斯定理是如何利用先验概率和后验概率进行概率更新的，尤其要注意其在实际应用中的价值。 4. 概率分布的掌握: 熟悉常见概率分布的公式和性质，并能进行简单的概率计算。 5. 随机变量的期望和方差: 掌握计算随机变量期望和方差的步骤，并了解它们在统计推断中的作用。 这份复习资料旨在帮助你快速掌握概率论的关键概念和技巧，祝你期末考试顺利！
展开
概率论
2025-04-17
2次阅读