第 1 页 / 共 34 页
第 2 页 / 共 34 页
第 3 页 / 共 34 页
第 4 页 / 共 34 页
第 5 页 / 共 34 页
第 6 页 / 共 34 页
第 7 页 / 共 34 页
第 8 页 / 共 34 页
第 9 页 / 共 34 页
第 10 页 / 共 34 页
第 11 页 / 共 34 页
第 12 页 / 共 34 页
第 13 页 / 共 34 页
第 14 页 / 共 34 页
第 15 页 / 共 34 页
第 16 页 / 共 34 页
第 17 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计复习整理 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 18 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计复习整理 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 19 页 / 共 34 页
第 20 页 / 共 34 页
第 21 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计复习整理 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 22 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计复习整理 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 23 页 / 共 34 页
第 24 页 / 共 34 页
第 25 页 / 共 34 页
第 26 页 / 共 34 页
第 27 页 / 共 34 页
第 28 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计复习整理 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 29 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计复习整理 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 30 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计复习整理 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 31 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计复习整理 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 32 页 / 共 34 页
第 33 页 / 共 34 页
第 34 页 / 共 34 页
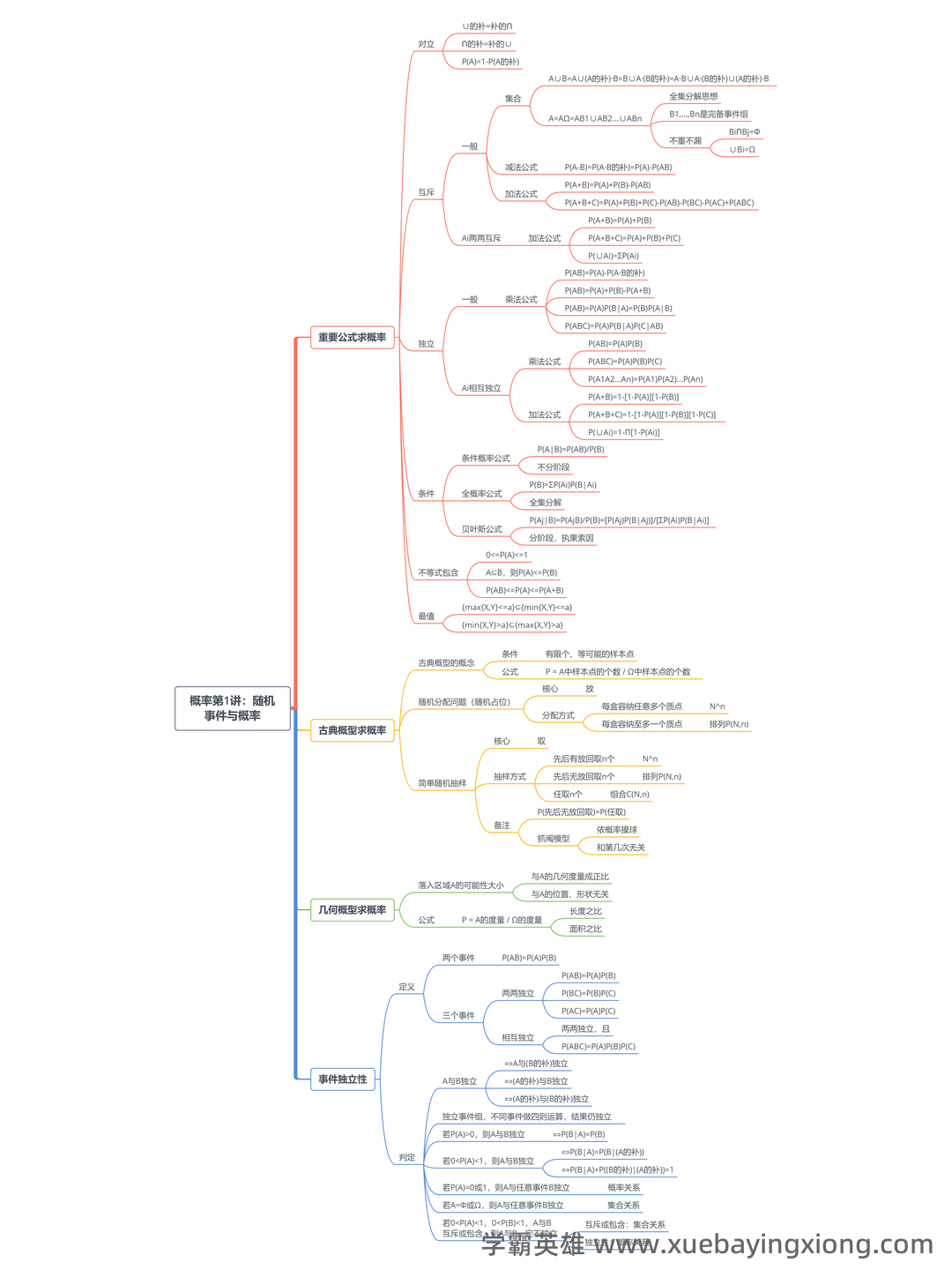
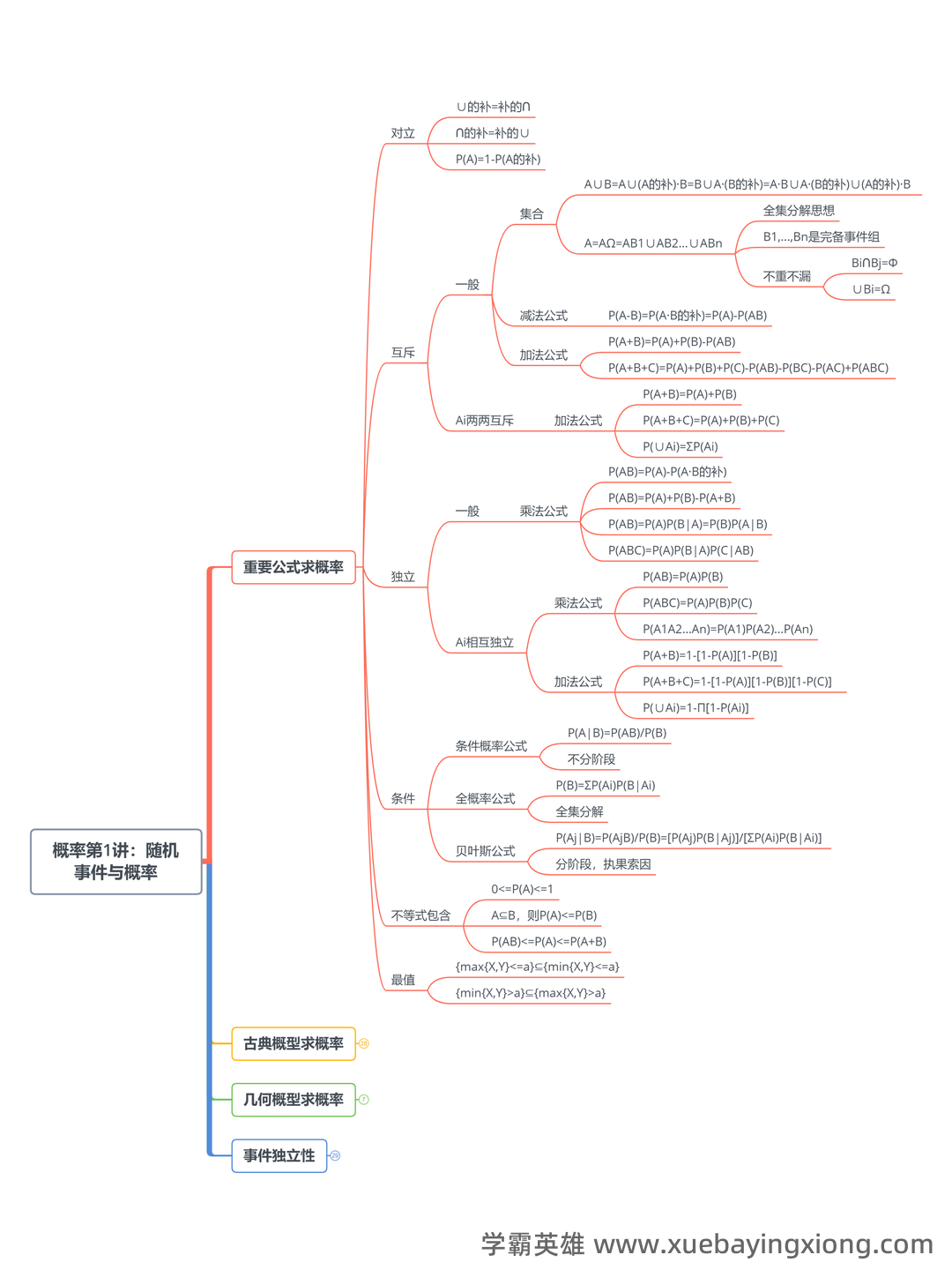
概率论与数理统计复习整理
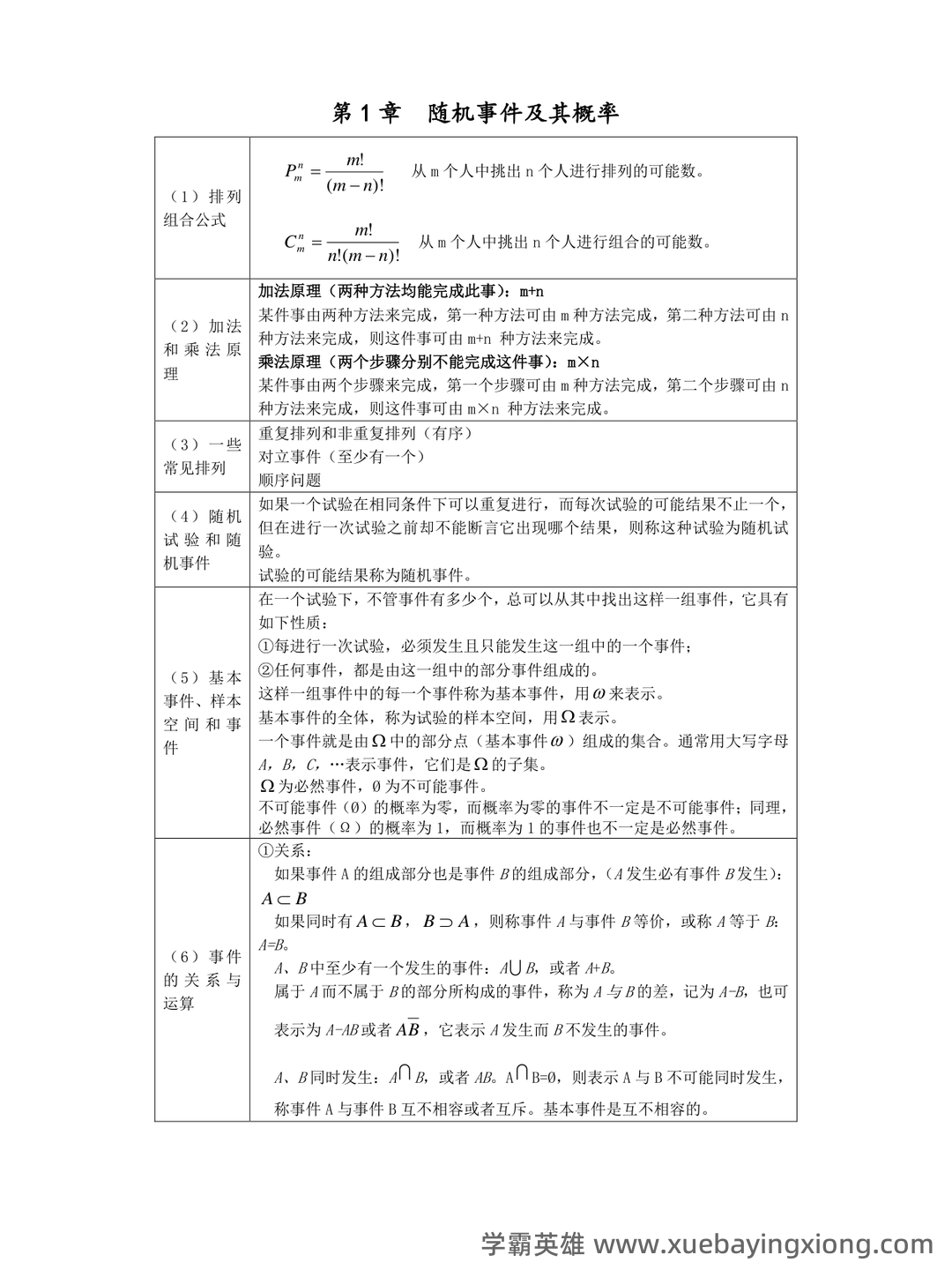
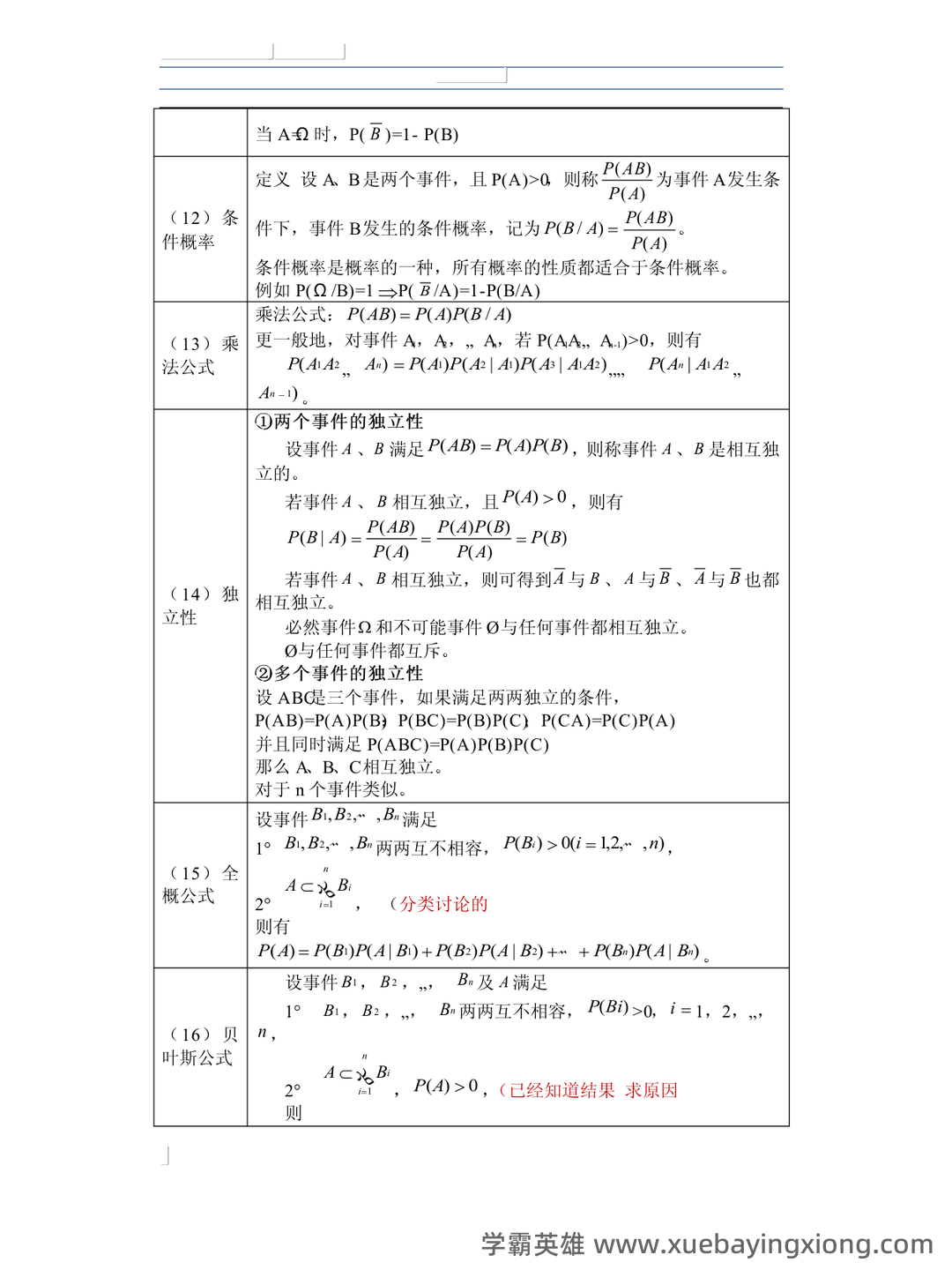
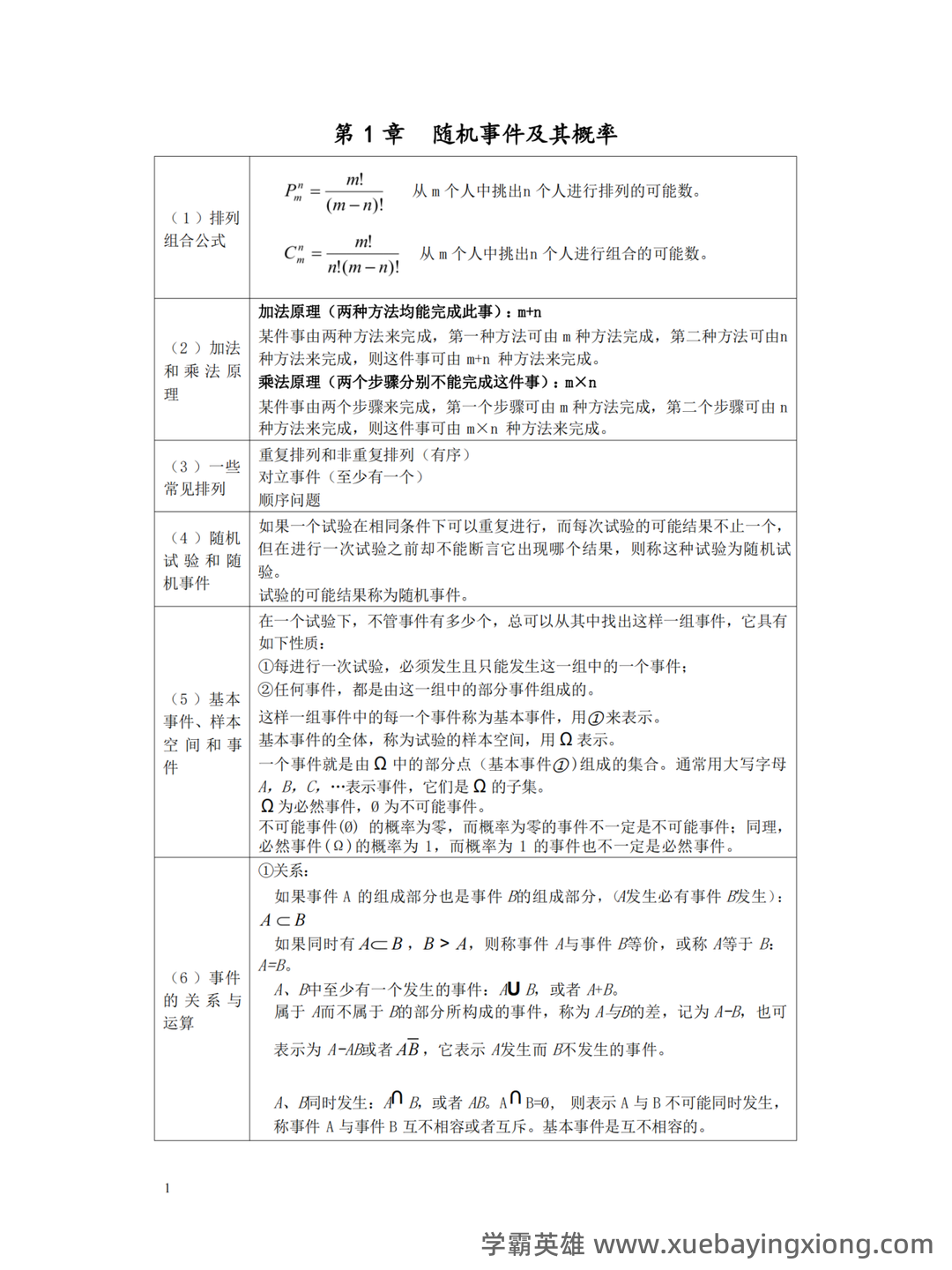
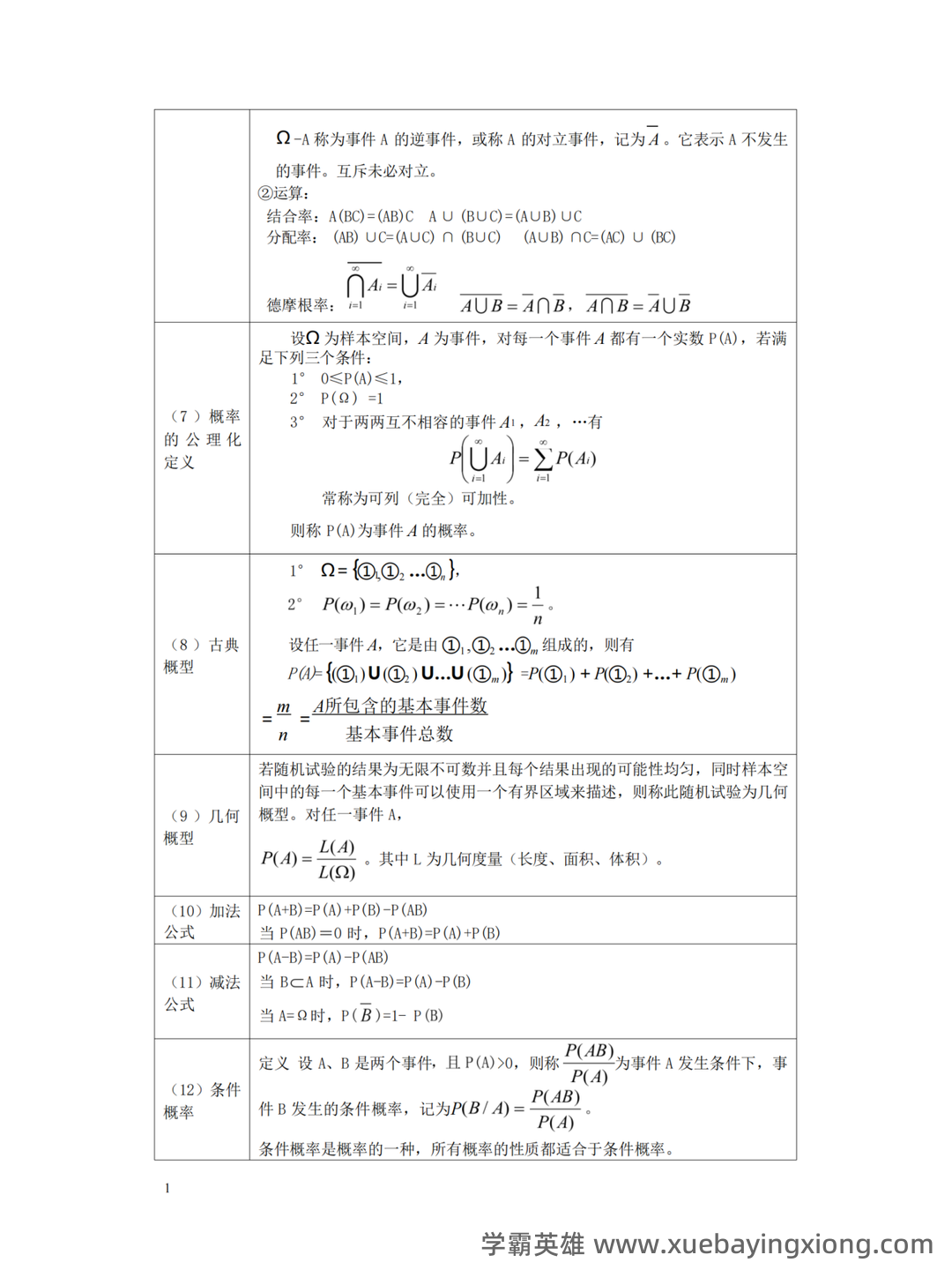
概率论与数理统计复习整理 概率论是描述随机现象及其规律的数学分支，而数理统计则运用概率论的方法对数据进行分析和解释。两者相互关联，共同构成了数据科学和相关领域的基础。 概率论核心概念回顾 概率定义: 概率是描述事件发生的可能性大小的指标，通常表示为0到1之间的数值。 随机变量: 表示不确定性量的变量，如均匀分布、正态分布、二项分布等。了解不同分布的特性及其参数至关重要。 条件概率: 在已知事件A发生的条件下，事件B发生的概率，记作P(B|A)。 理解条件概率在解决实际问题中的应用是核心。 贝叶斯定理: 用于根据新的证据更新对一个事件的概率估计，公式为：P(A|B) = [P(B|A) P(A)] / P(B)。 期望、方差、标准差: 衡量随机变量集中程度的指标，对理解和应用概率分布至关重要。 数理统计基础概念回顾 描述性统计: 通过均值、方差、标准差等来描述数据集的特征。 推论统计: 利用样本数据推断总体特征，包括： 抽样分布: 在大量重复抽样后，样本统计量的分布。 置信区间: 对总体参数的估计范围，提供一定置信水平的保证。 假设检验: 通过比较样本数据与零假设的差异，来判断总体特征是否存在显著差异。 掌握概率论与数理统计的核心概念，并将其灵活运用，能够帮助我们更好地理解和处理各种数据，做出更准确的判断和决策。 持续学习和实践是提升概率论与数理统计技能的关键。
展开
概率论
2025-04-17
20次阅读