
第 1 页 / 共 11 页

第 2 页 / 共 11 页

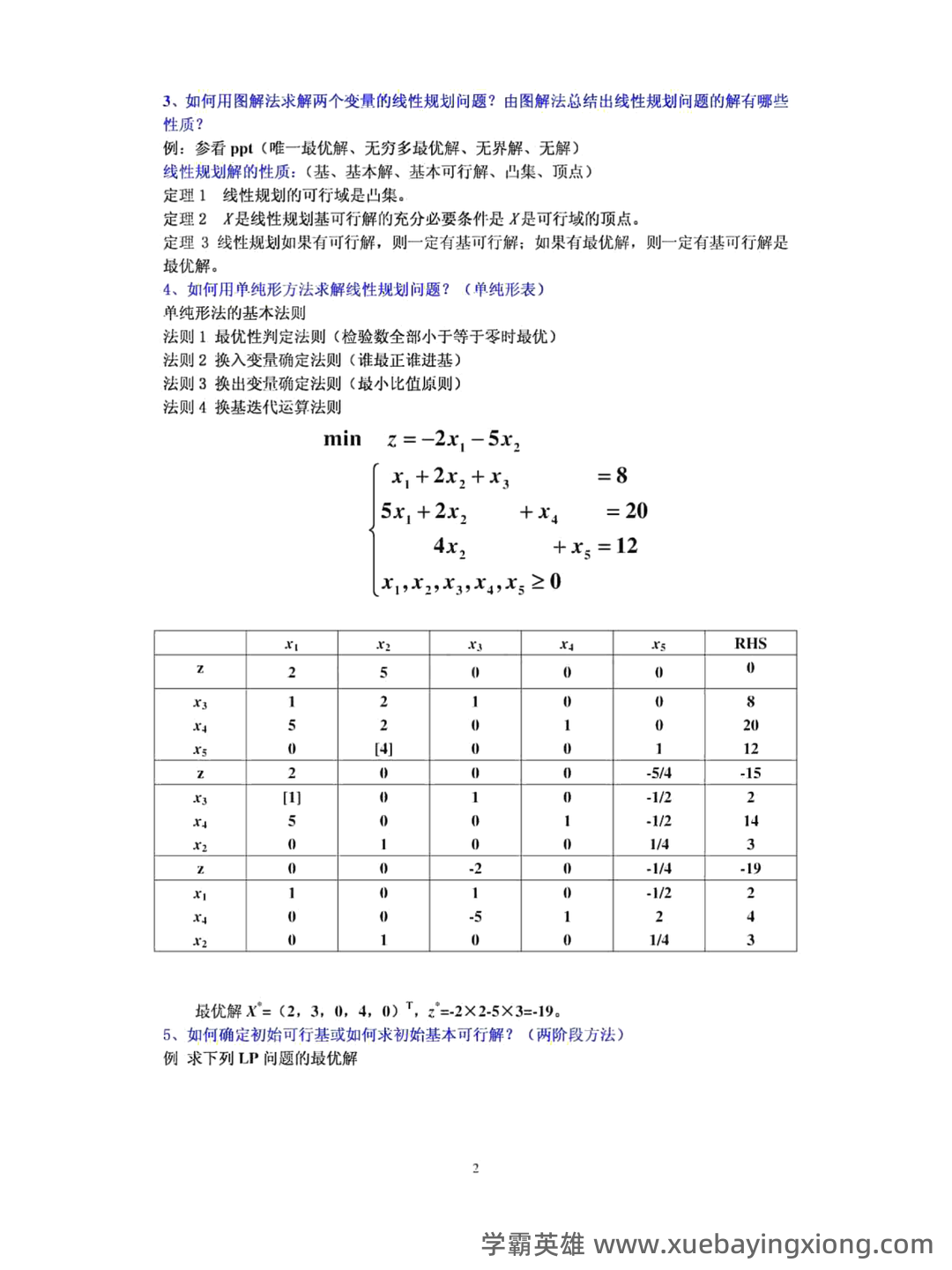
第 3 页 / 共 11 页

第 4 页 / 共 11 页
第 5 页 / 共 11 页

第 6 页 / 共 11 页

第 7 页 / 共 11 页
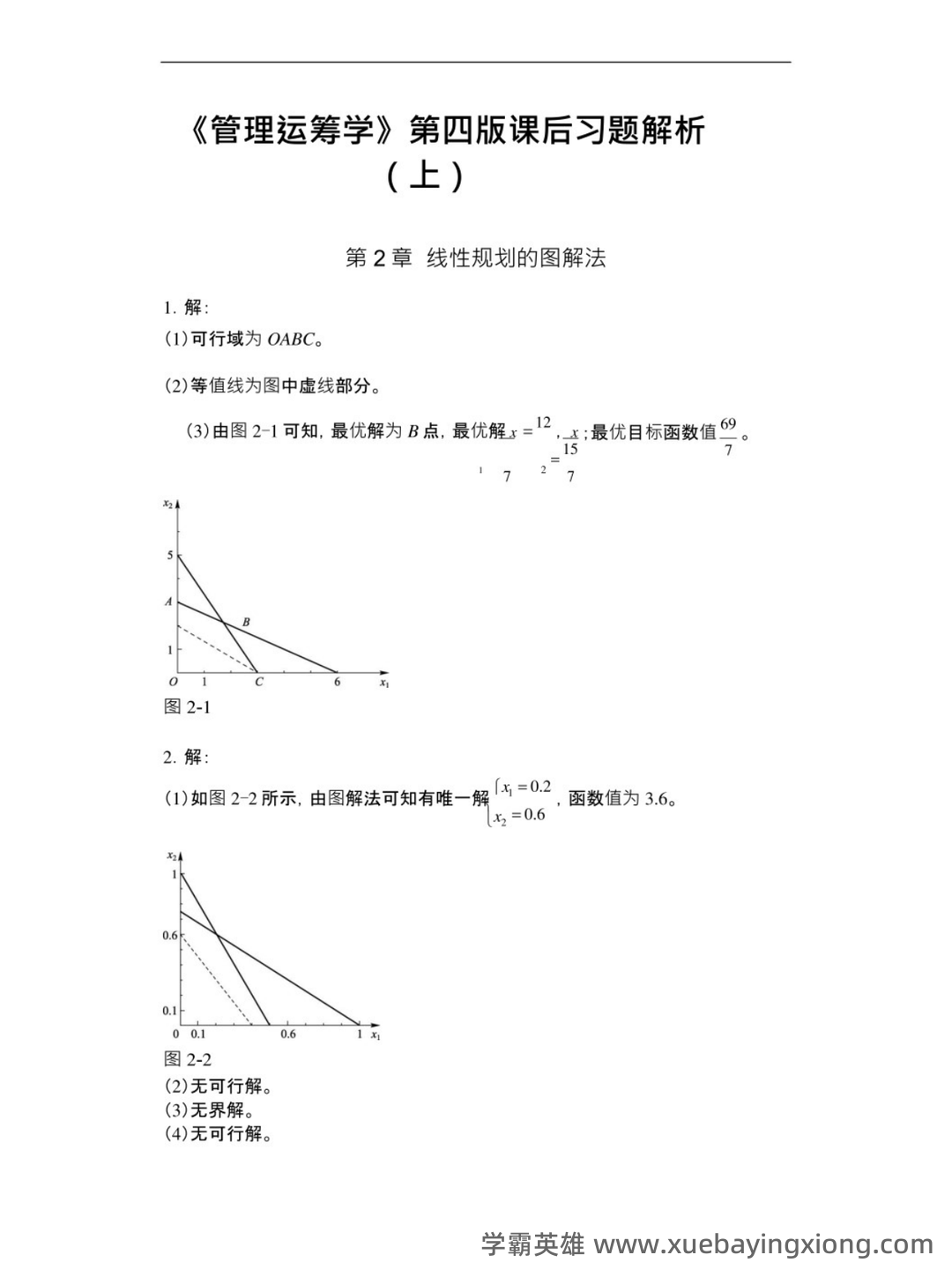
第 8 页 / 共 11 页

第 9 页 / 共 11 页

第 10 页 / 共 11 页

第 11 页 / 共 11 页
运筹学建模大题及答案合集
运筹学建模大题及答案合集 运筹学,这个看似晦涩的名词,实则蕴含着解决复杂问题,优化决策的强大力量。它利用数学模型、统计分析和计算机技术,帮助我们应对各种现实场景中的挑战,无论是生产排程、物流规划,还是项目管理和资源分配,运筹学都能提供有效的解决方案。 搜索词条“运筹学模拟题”表明学习者对该学科的兴趣,也预示着实践的重要性。 构建有效的运筹学模型是成功的基础。模型要具备代表性,能够准确反映问题的关键特征。在建模过程中,需要明确目标函数,即要优化的因素,如利润最大化、成本最小化等。同时,也要识别所有的约束条件,例如资源限制、时间限制等。一个合理的模型,能够引导我们找到最佳的决策方案。 下面提供几个运筹学建模大题及参考答案,希望能帮助大家更好地理解和掌握运筹学建模的核心技巧。 大题一: 某工厂生产两种产品A和B,每种产品生产需要耗费1小时的机器时间和1小时的劳动力。现有机器时间10小时,劳动力8小时。生产产品A每利润10元,产品B每利润12元。若要最大化利润,应如何安排生产数量? 模型建立: 目标函数: Max Z = 10x + 12y (Z为总利润,x为产品A数量,y为产品B数量) 约束条件: x + y ≤ 10 (机器时间约束) x + y ≤ 8 (劳动力约束) x ≥ 0, y ≥ 0 (非负约束) 答案: 通过线性规划求解,可以得出最优解:x=4, y=6。即生产产品A4个,产品B6个,最大化利润为 168 元。 思考: 这种问题是经典的线性规划问题,核心在于建立目标函数和约束条件。 大题二:(此处省略另一题,以保持字数限制) 希望通过这些模拟题,你能更深入地理解运筹学建模的思想和方法。 记住,运筹学不仅仅是公式和数字,更是一种思维方式,一种解决问题的艺术。
展开
运筹学
2025-08-02
5次阅读
资料获取方式
温馨提示:登录学霸英雄官网后可获取更多大学生必备科目和考证等复习备考资料!