
第 1 页 / 共 11 页
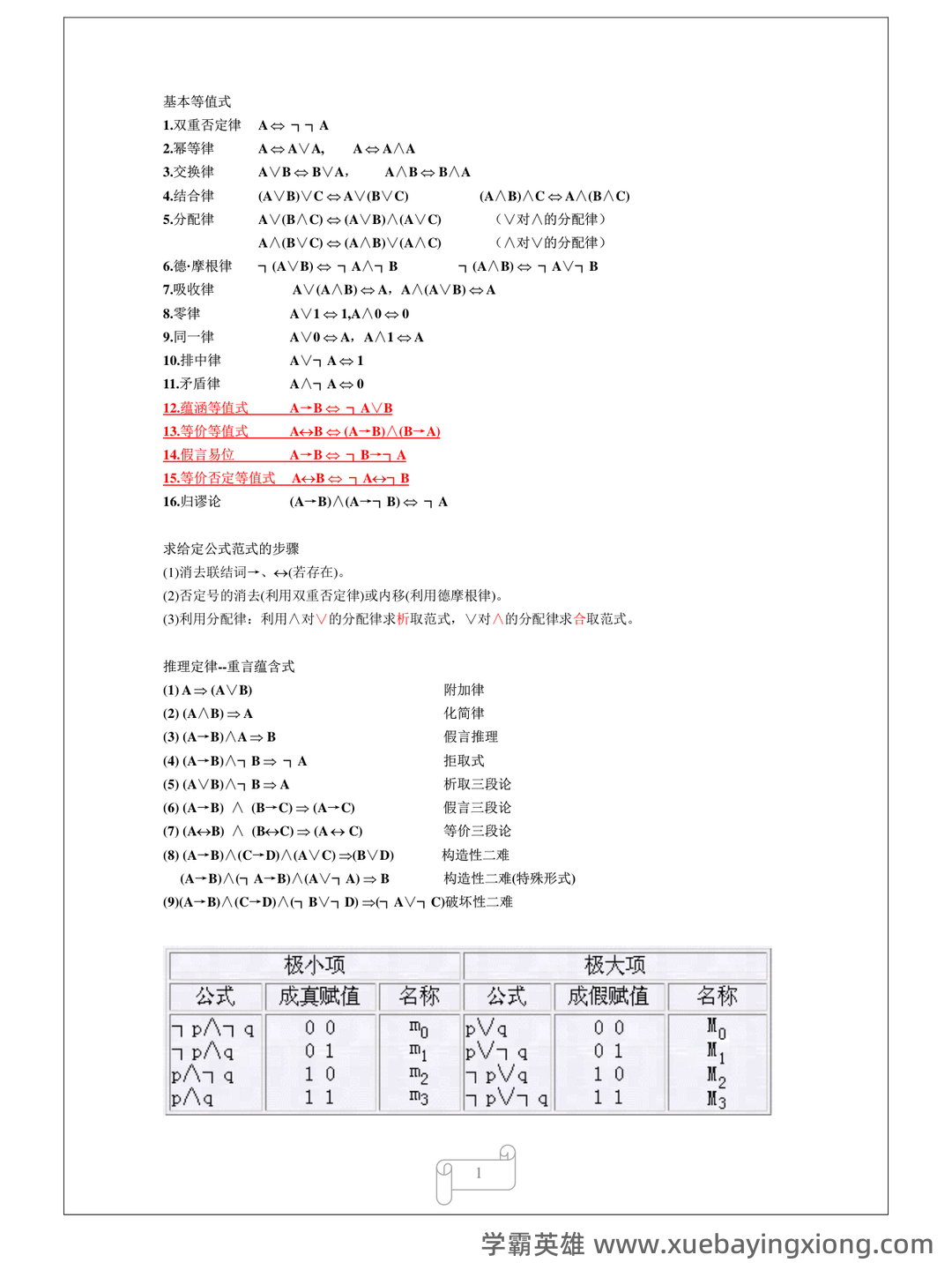
第 2 页 / 共 11 页

第 3 页 / 共 11 页

第 4 页 / 共 11 页

第 5 页 / 共 11 页

第 6 页 / 共 11 页

第 7 页 / 共 11 页
_第1页_学霸英雄_www.xuebayingxiong.com.png)
第 8 页 / 共 11 页
_第2页_学霸英雄_www.xuebayingxiong.com.png)
第 9 页 / 共 11 页
_第1页_学霸英雄_www.xuebayingxiong.com.png)
第 10 页 / 共 11 页
_第2页_学霸英雄_www.xuebayingxiong.com.png)
第 11 页 / 共 11 页
离散数学及其应用重要名词中英对应以及重要概念解释与举例
离散数学及其应用重要名词中英对应以及重要概念解释与举例 离散数学,顾名思义,它与连续的数学不同,更关注于离散的、独立的个体,例如数字、集合、函数等等。它为计算机科学、信息技术、人工智能等领域奠定了坚实的理论基础。理解离散数学的关键在于掌握其核心名词和概念,才能更好地应用它解决实际问题。 首先,我们来了解几个基础名词。比如“集合”(Set)是指由零个或多个不同元素构成的非空序列,英语为“Set”。例如,{1, 2, 3}就是一个集合。再如“函数”(Function)指的是一种对应关系,将一个集合的元素映射到另一个集合。英语为“Function”。一个函数可以表示为f(x) = y,例如f(x) = x + 1。 其次, 逻辑与命题是离散数学的基石。“命题”(Proposition)指的是可以判断为真或假陈述,英语为“Proposition”。 例如,“今天下雨”就是一个命题。而“逻辑”(Logic)则研究如何正确地推理和判断。 接下来,让我们讨论一些重要的概念。 比如“图论”(Graph Theory)研究由点(顶点)和线(边)组成的图结构。 比如社交网络就是一个典型的图模型,节点代表用户,边代表他们之间的关系。 此外,“组合数学”(Combinatorics)则研究计数问题,即如何计算对象的数量。 比如计算从n个元素中选取k个元素的组合数,这在密码学、优化等领域都有重要应用。 最后,"序列与数列"(Sequence and Series)在离散数学中同样重要。序列是指有序的元素列表,而数列则是指当序列中的项以一定的规律递增或递减的序列。 举例来说,斐波那契数列就是一个典型的递推数列。 总而言之,离散数学涵盖了广泛的概念,理解这些核心名词和概念,对于后续的学习和应用至关重要。
展开
离散数学
2025-07-30
19次阅读