
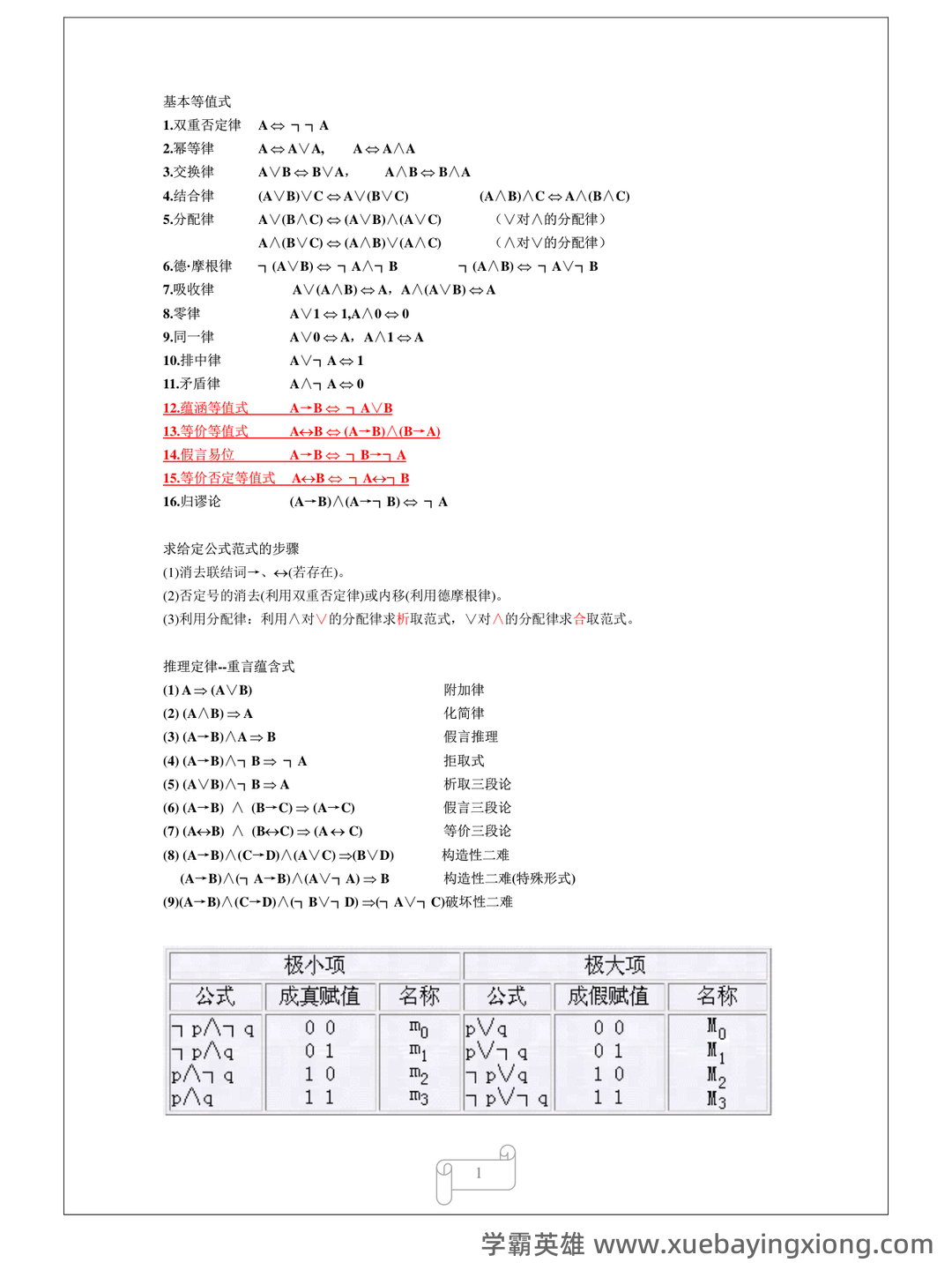
第 1 页 / 共 11 页
第 2 页 / 共 11 页

第 3 页 / 共 11 页

第 4 页 / 共 11 页

第 5 页 / 共 11 页

第 6 页 / 共 11 页

第 7 页 / 共 11 页
_第1页_学霸英雄_www.xuebayingxiong.com.png)
第 8 页 / 共 11 页
_第2页_学霸英雄_www.xuebayingxiong.com.png)
第 9 页 / 共 11 页
_第1页_学霸英雄_www.xuebayingxiong.com.png)
第 10 页 / 共 11 页
_第2页_学霸英雄_www.xuebayingxiong.com.png)
第 11 页 / 共 11 页
离散数学(上)模拟题
离散数学(上)模拟题 离散数学,这个词听起来可能有点高深莫测,但其实它涵盖了我们日常生活中大量的基础概念和逻辑思维。尤其是“离散数学模拟题”这一关键词,正是帮助我们系统梳理和掌握这门学科的关键所在。这部分模拟题通常会聚焦于集合论、关系、函数等核心内容,是打好基础的敲门砖。 集合论是离散数学的基石。理解集合、子集、交集、并集等概念,对于后续学习至关重要。要知道,很多算法的设计和分析都离不开集合论的原理。想象一下,在数据库管理中,如何高效地存储和检索数据,就离不开对集合操作的熟练运用。 接下来,关系和函数这两个概念也至关重要。关系可以看作是集合之间的联系,而函数则是定义了输入和输出之间对应关系的特殊函数。理解函数的单调性、奇偶性,以及函数的复合,都能帮助我们更好地理解数学模型。 现在,我们来做几道简单的题: 1. 如果A={1,2,3}, B={2,3,4}, 则 A∩B等于? (A) {1,2,3} (B) {2,3} (C) {} (D) {1,2,3,4} 2. 如果 f(x) = 2x + 1,则 f(3)等于? 3. 已知集合 U = {a, b, c, d, e},A = {a, b},B = {b, c},则 A∪B等于? 这几道题虽然简单,但却能检验你对这些基本概念的理解程度。认真思考,相信你一定能找到正确答案。祝你学习愉快!
展开
离散数学
2025-07-30
48次阅读