第 1 页 / 共 11 页
第 2 页 / 共 11 页
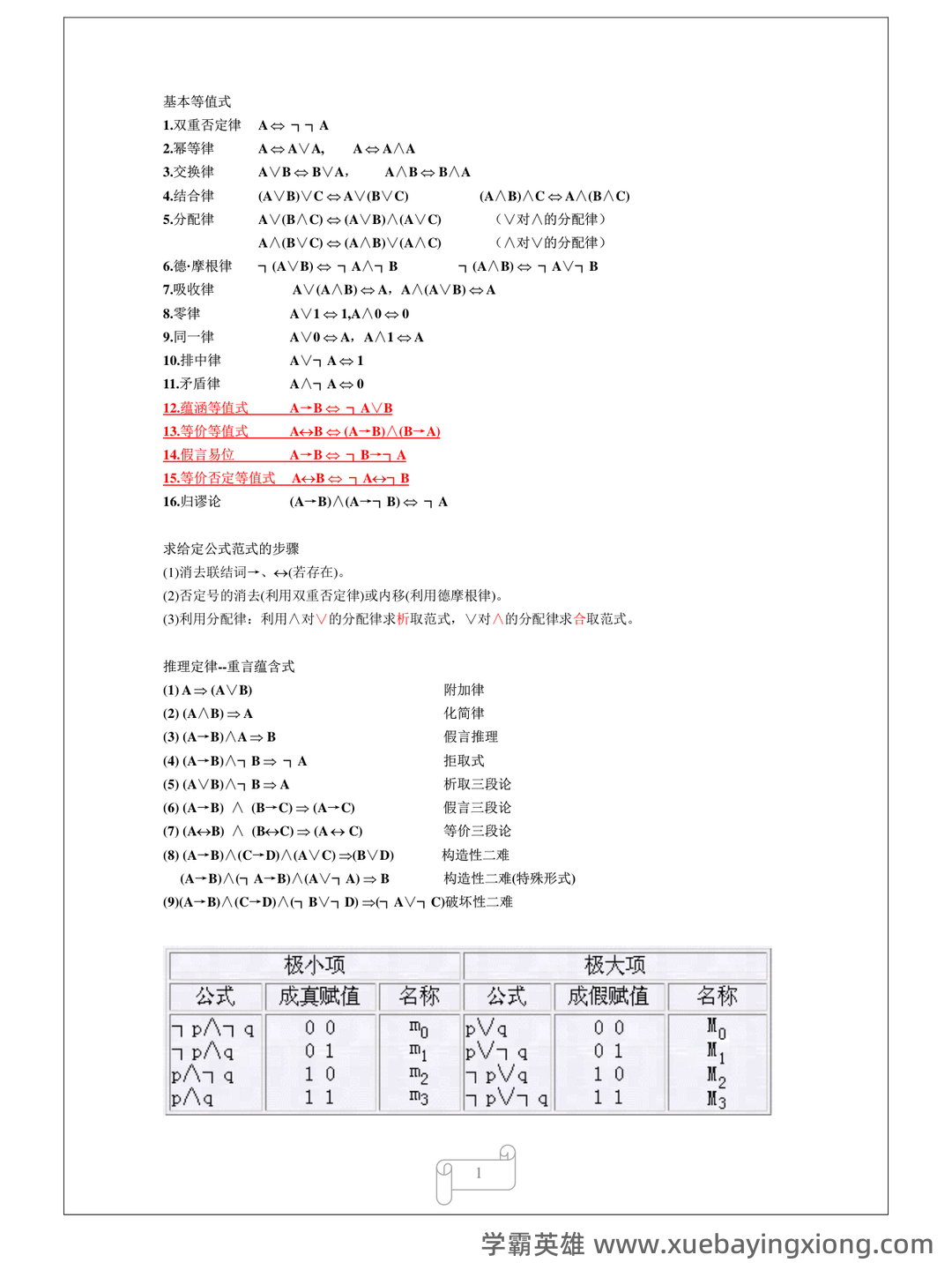
第 3 页 / 共 11 页
第 4 页 / 共 11 页
第 5 页 / 共 11 页
第 6 页 / 共 11 页
第 7 页 / 共 11 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "总结 离散数学知识点 - hjlweilong - - 04_《离散数学》复习资料_《离散数学》课后习题答案-(左孝凌版)_第1页_学霸英雄_www.xuebayingxiong.com")
第 8 页 / 共 11 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "总结 离散数学知识点 - hjlweilong - - 04_《离散数学》复习资料_《离散数学》课后习题答案-(左孝凌版)_第2页_学霸英雄_www.xuebayingxiong.com")
第 9 页 / 共 11 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "总结 离散数学知识点 - hjlweilong - - 05_《离散数学》复习资料_《离散数学》部分概念和公式总结(考试专用)_第1页_学霸英雄_www.xuebayingxiong.com")
第 10 页 / 共 11 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "总结 离散数学知识点 - hjlweilong - - 05_《离散数学》复习资料_《离散数学》部分概念和公式总结(考试专用)_第2页_学霸英雄_www.xuebayingxiong.com")
第 11 页 / 共 11 页
总结 离散数学知识点 - hjlweilong -
总结 离散数学知识点 - hjlweilong - 离散数学，听起来是不是有点高深莫测？其实它就像是构建现代计算机科学、信息技术、人工智能等领域基石的砖块。它研究的是不能连续的对象，比如数字、集合、关系、图论等等。掌握离散数学，就像掌握了理解这些底层逻辑的关键。 首先，集合论是离散数学的基石。它研究的是集合的概念，包括集合的定义、运算（交集、并集、补集等）和集合的性质。理解集合论，能帮助我们更清晰地表达和思考问题，尤其是在逻辑推理和算法设计中。 其次，逻辑学是离散数学的重要组成部分。它研究的是命题、谓词、量词等，以及它们的逻辑关系。 掌握基本的逻辑规则，如否定律、合取律、析取律，能够帮助我们进行严谨的推理和证明。 再者，图论则是一种研究网络结构的学科。它研究的是节点和边之间的关系，用于建模各种网络系统，例如社交网络、交通网络、电路网络等等。 掌握图的表示方法、遍历算法，是解决实际问题的关键。 此外，数理逻辑也是离散数学的重要分支。它研究的是命题逻辑、谓词逻辑、证明方法等，对于计算机程序的正确性验证、算法设计等都有着重要的指导意义。 最后，一些重要的数学概念，比如马尔可夫链、状态空间，也属于离散数学的范畴。它们在概率论、时间序列分析、网络动力学等领域有着广泛的应用。 离散数学的学习，需要结合实际问题进行思考，并不断地进行练习和总结，才能真正掌握其精髓。
展开
离散数学
2025-07-30
7次阅读
资料获取方式
温馨提示：登录学霸英雄官网后可获取更多大学生必备科目和考证等复习备考资料！