
第 1 页 / 共 11 页
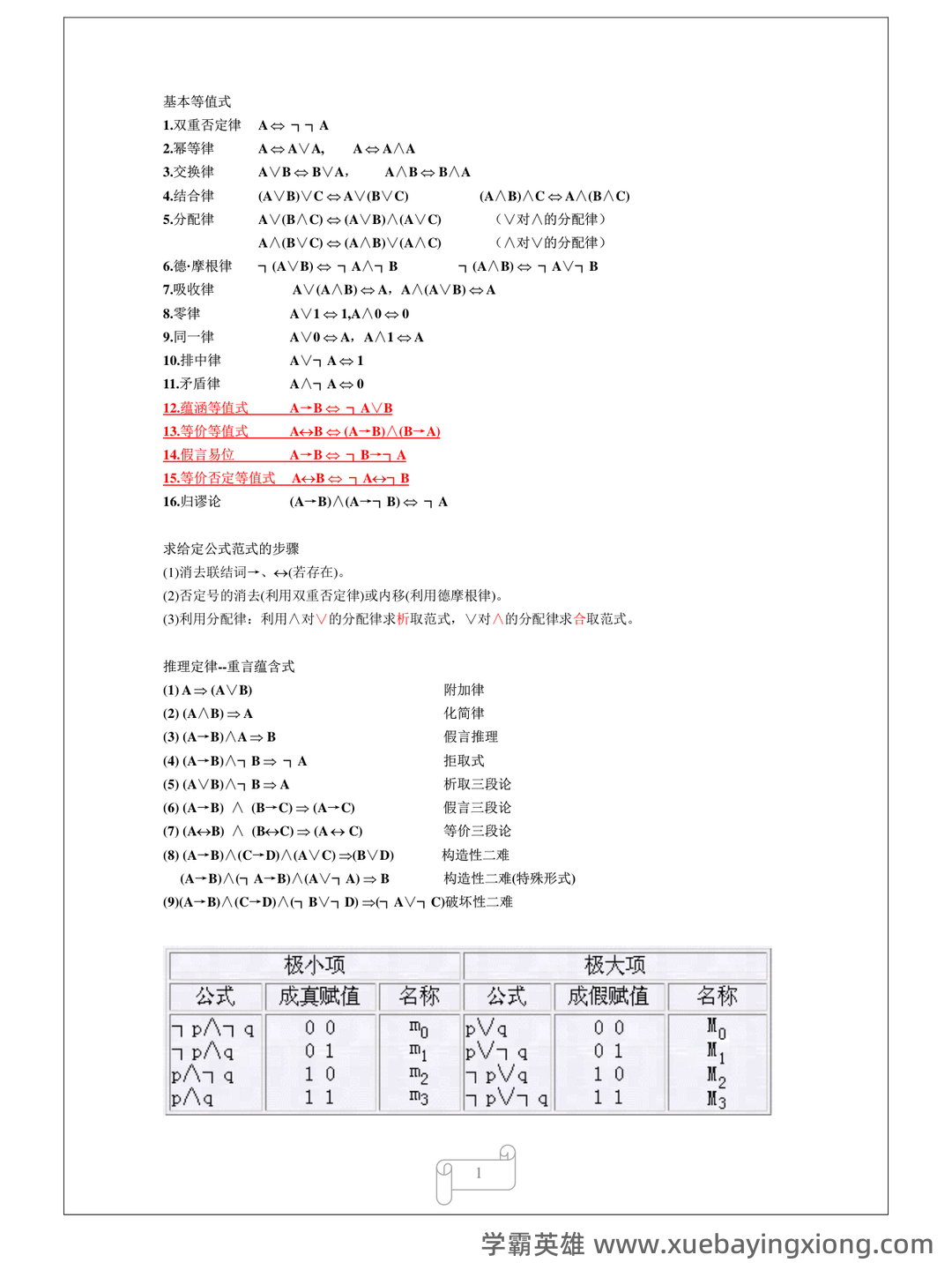
第 2 页 / 共 11 页

第 3 页 / 共 11 页

第 4 页 / 共 11 页

第 5 页 / 共 11 页

第 6 页 / 共 11 页

第 7 页 / 共 11 页
_第1页_学霸英雄_www.xuebayingxiong.com.png)
第 8 页 / 共 11 页
_第2页_学霸英雄_www.xuebayingxiong.com.png)
第 9 页 / 共 11 页
_第1页_学霸英雄_www.xuebayingxiong.com.png)
第 10 页 / 共 11 页
_第2页_学霸英雄_www.xuebayingxiong.com.png)
第 11 页 / 共 11 页
离散数学知识点梳理
离散数学知识点梳理 离散数学,顾名思义,它不像连续数学那样关注无穷大、连续变化,而是研究离散、有限的数学对象。它在计算机科学、信息技术、密码学等领域有着广泛的应用,理解它的核心知识点,对于我们在这些领域打下坚实的基础至关重要。 首先,集合论是离散数学的基石。它研究集合及其运算,比如并集、交集、补集等等。 掌握集合的定义、运算规则,是理解后续知识的基础。 “集合论,是构建整个离散数学体系的骨架” 就像盖房子需要地基一样。 其次,逻辑学是另一个重要的组成部分。 学习命题逻辑、谓词逻辑,能够帮助我们清晰地表达思想,并进行严谨的推理。 掌握真值表、推理规则,能够让我们避免逻辑谬误,提升思考的严谨性。 再者,图论是研究图中节点和边及其关系的学科。 学习图的表示方法、基本图论算法(如最短路径、最小生成树),对于解决实际问题具有重要意义。 比如在网络路由、社交网络分析等方面。 此外,关系论、数论以及代数概数,也都是离散数学中重要的分支。 学习它们能够帮助我们更深入地理解数字、关系、函数等概念。 比如数论中,质数、合数、同余等概念,是理解密码学的基础。 最后,函数理论是理解离散数学的重要组成部分,涉及一对多、多对多等各种函数类型。 掌握函数定义、图像、性质等等,对于理解计算机程序、算法设计都非常重要。 学习过程中,多做练习,熟练掌握各种算法和模型,才能真正掌握离散数学的精髓。
展开
离散数学
2025-07-30
7次阅读
资料获取方式
温馨提示:登录学霸英雄官网后可获取更多大学生必备科目和考证等复习备考资料!