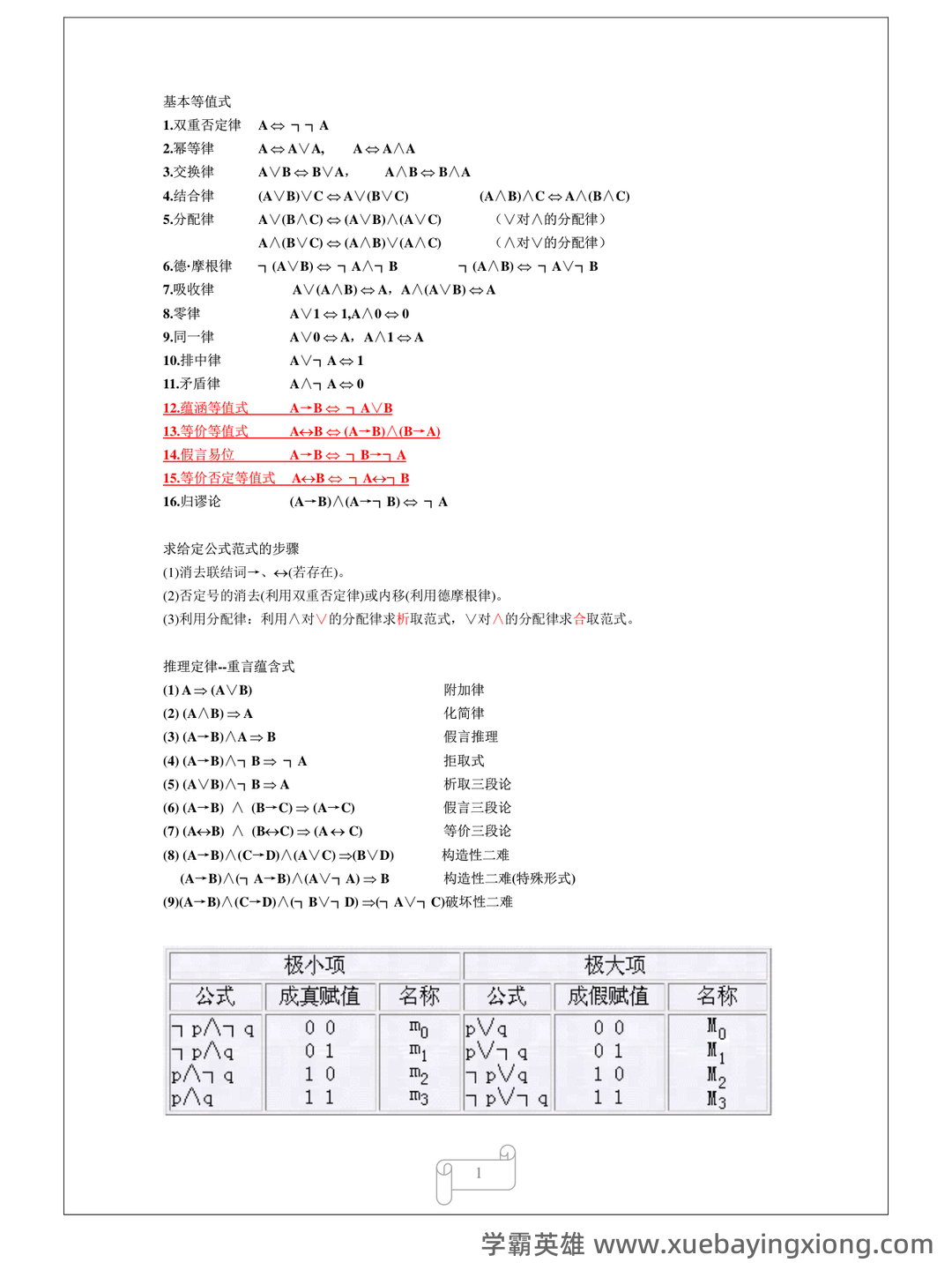
第 1 页 / 共 11 页
第 2 页 / 共 11 页
第 3 页 / 共 11 页
第 4 页 / 共 11 页
第 5 页 / 共 11 页
第 6 页 / 共 11 页
第 7 页 / 共 11 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "【离散数学】期末不挂科复习笔记_部分否定等值式离散数学量词 - 04_《离散数学》复习资料_《离散数学》课后习题答案-(左孝凌版)_第1页_学霸英雄_www.xuebayingxiong.com")
第 8 页 / 共 11 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "【离散数学】期末不挂科复习笔记_部分否定等值式离散数学量词 - 04_《离散数学》复习资料_《离散数学》课后习题答案-(左孝凌版)_第2页_学霸英雄_www.xuebayingxiong.com")
第 9 页 / 共 11 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "【离散数学】期末不挂科复习笔记_部分否定等值式离散数学量词 - 05_《离散数学》复习资料_《离散数学》部分概念和公式总结(考试专用)_第1页_学霸英雄_www.xuebayingxiong.com")
第 10 页 / 共 11 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "【离散数学】期末不挂科复习笔记_部分否定等值式离散数学量词 - 05_《离散数学》复习资料_《离散数学》部分概念和公式总结(考试专用)_第2页_学霸英雄_www.xuebayingxiong.com")
第 11 页 / 共 11 页
【离散数学】期末不挂科复习笔记_部分否定等值式离散数学量词
【离散数学】期末不挂科复习笔记_部分否定等值式 离散数学，听起来是不是有点唬人？其实，它就像一个有趣的拼图，需要我们慢慢拼凑出逻辑、集合、函数、图论等各种知识。期末考试，咱们得好好复习一下，避免那句“哎呀，挂科了…”的尴尬。 今天咱们重点关注的是“部分否定等值式”，这绝对是离散数学中一些奇妙的逻辑规则。 掌握这些规则，就像拥有了解题的钥匙，能帮你更快更准确地得出结论。 首先，理解“部分否定”的概念非常关键。 否定全句，意味着否定句中的所有组成部分。 但部分否定，则只否定了句子的部分组成部分，剩下的部分则保持不变。 例如：“并非所有人都喜欢冰淇淋”可以写成“并非所有人都是冰淇淋爱好者”。 接下来， 让我们看看一些常见的等值式： ¬(∀x P(x)) ≡ ∃x ¬P(x) – “并非所有 x 都满足 P(x)” 等价于 “存在一个 x 不满足 P(x)” ¬(∃x P(x)) ≡ ∀x ¬P(x) – “存在一个 x 不满足 P(x)” 等价于 “所有 x 都不满足 P(x)” 这些等值式看似复杂，但其实就是逻辑的转换。 多做一些例题，你会发现它们的应用非常广泛，尤其是在证明题中，能够帮助你更简洁地表达你的思路。 记住，理解是关键，熟练运用才是王道！ 相信你只要用心学习，一定能期末考试取得好成绩！
展开
离散数学
2025-07-30
8次阅读
资料获取方式
温馨提示：登录学霸英雄官网后可获取更多大学生必备科目和考证等复习备考资料！