第 1 页 / 共 34 页
第 2 页 / 共 34 页
第 3 页 / 共 34 页
第 4 页 / 共 34 页
第 5 页 / 共 34 页
第 6 页 / 共 34 页
第 7 页 / 共 34 页
第 8 页 / 共 34 页
第 9 页 / 共 34 页
第 10 页 / 共 34 页
第 11 页 / 共 34 页
第 12 页 / 共 34 页
第 13 页 / 共 34 页
第 14 页 / 共 34 页
第 15 页 / 共 34 页
第 16 页 / 共 34 页
第 17 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】1.5 独立性_概率论与数理统计名词解释 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 18 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】1.5 独立性_概率论与数理统计名词解释 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 19 页 / 共 34 页
第 20 页 / 共 34 页
第 21 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】1.5 独立性_概率论与数理统计名词解释 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 22 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】1.5 独立性_概率论与数理统计名词解释 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 23 页 / 共 34 页
第 24 页 / 共 34 页
第 25 页 / 共 34 页
第 26 页 / 共 34 页
第 27 页 / 共 34 页
第 28 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】1.5 独立性_概率论与数理统计名词解释 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 29 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】1.5 独立性_概率论与数理统计名词解释 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 30 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】1.5 独立性_概率论与数理统计名词解释 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 31 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "【概率论与数理统计】1.5 独立性_概率论与数理统计名词解释 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 32 页 / 共 34 页
第 33 页 / 共 34 页
第 34 页 / 共 34 页
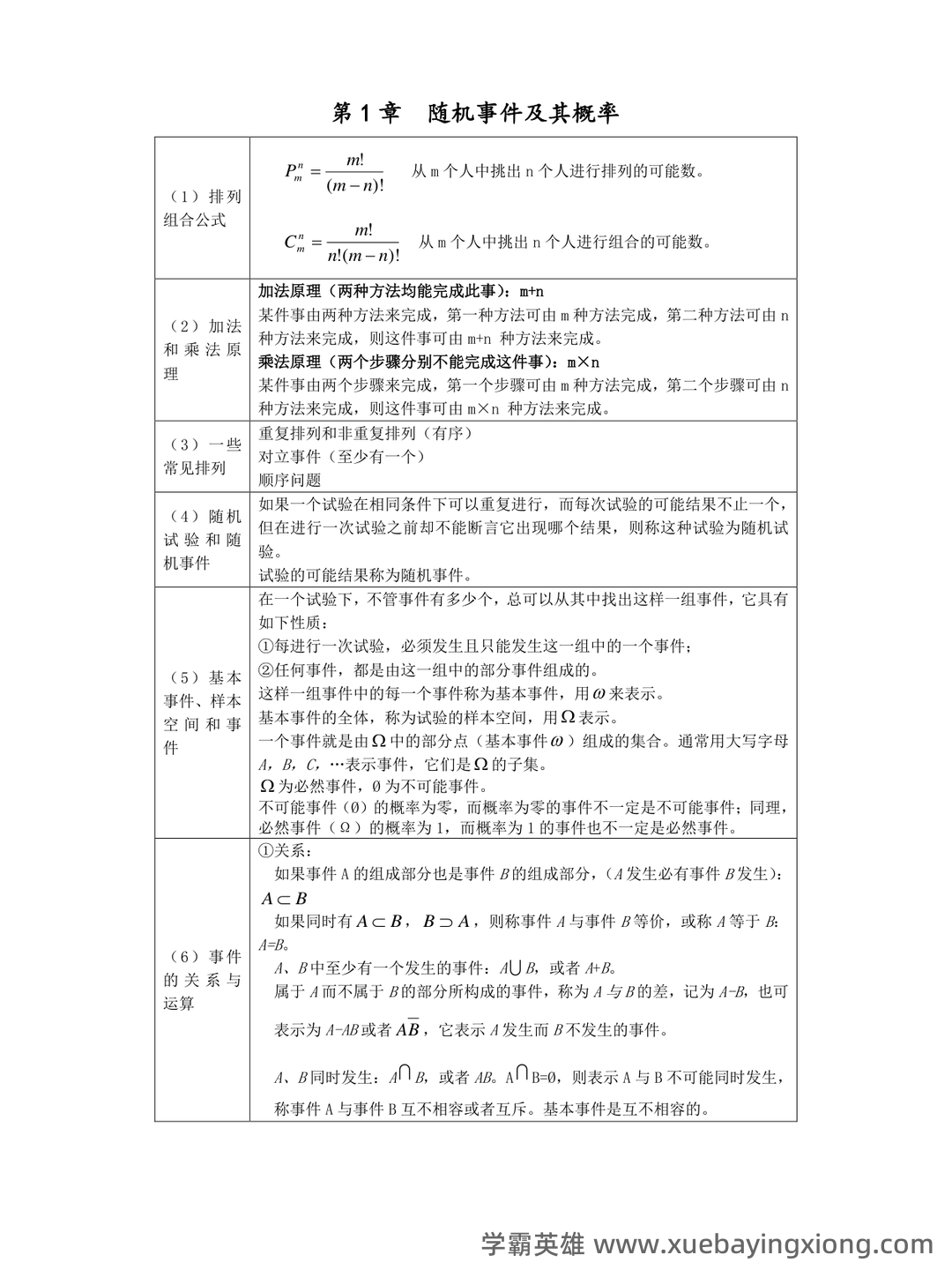
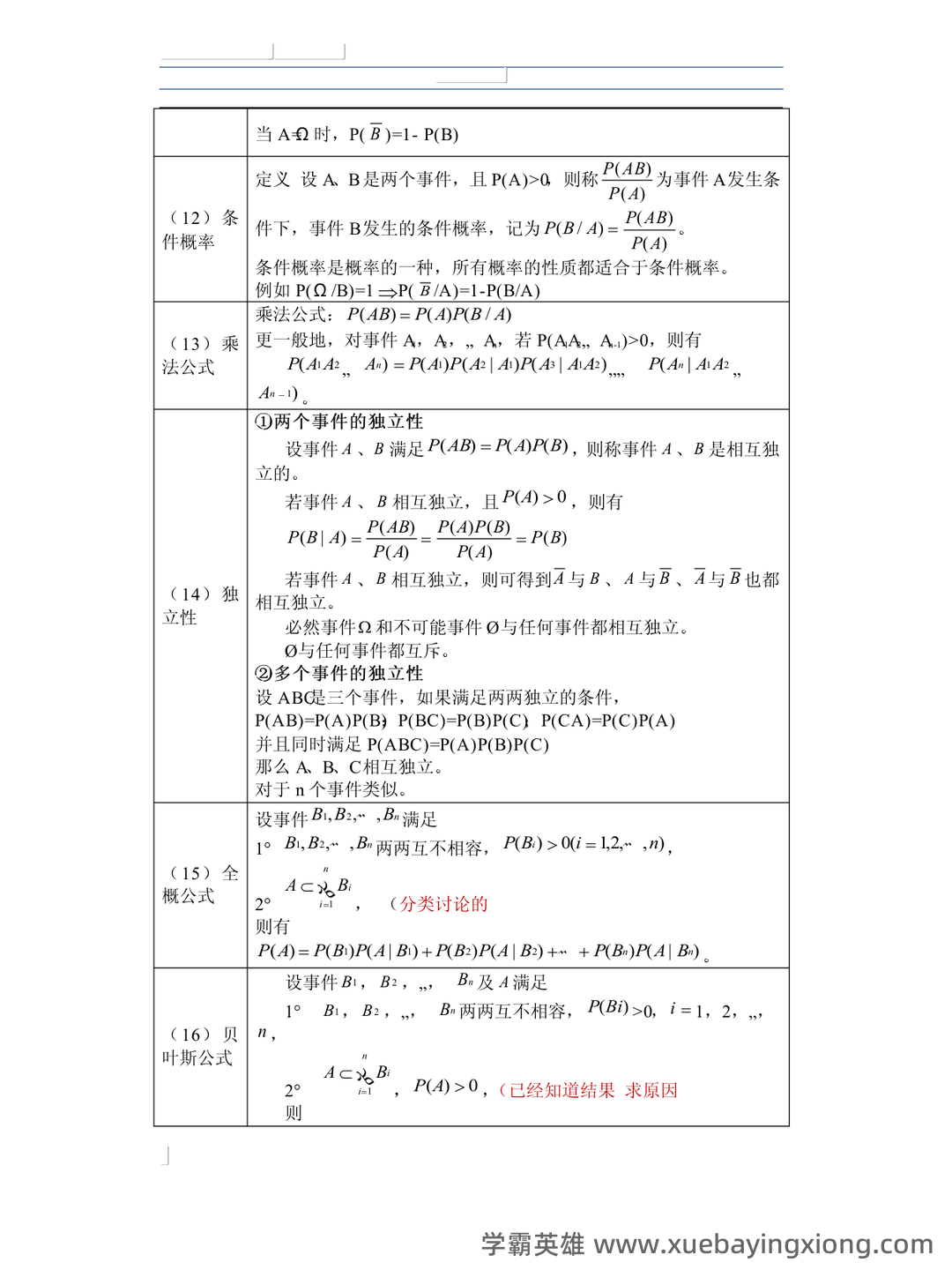
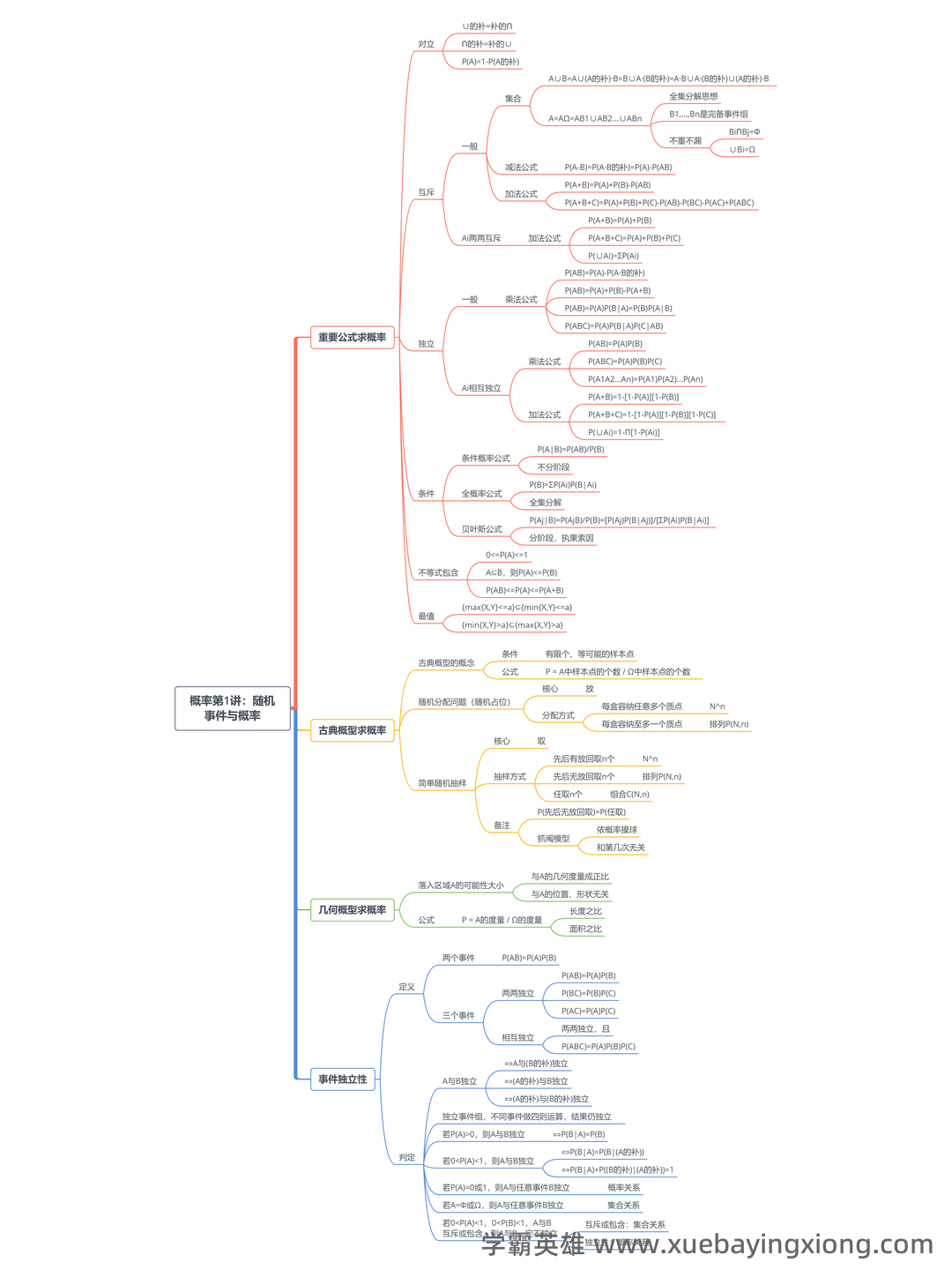
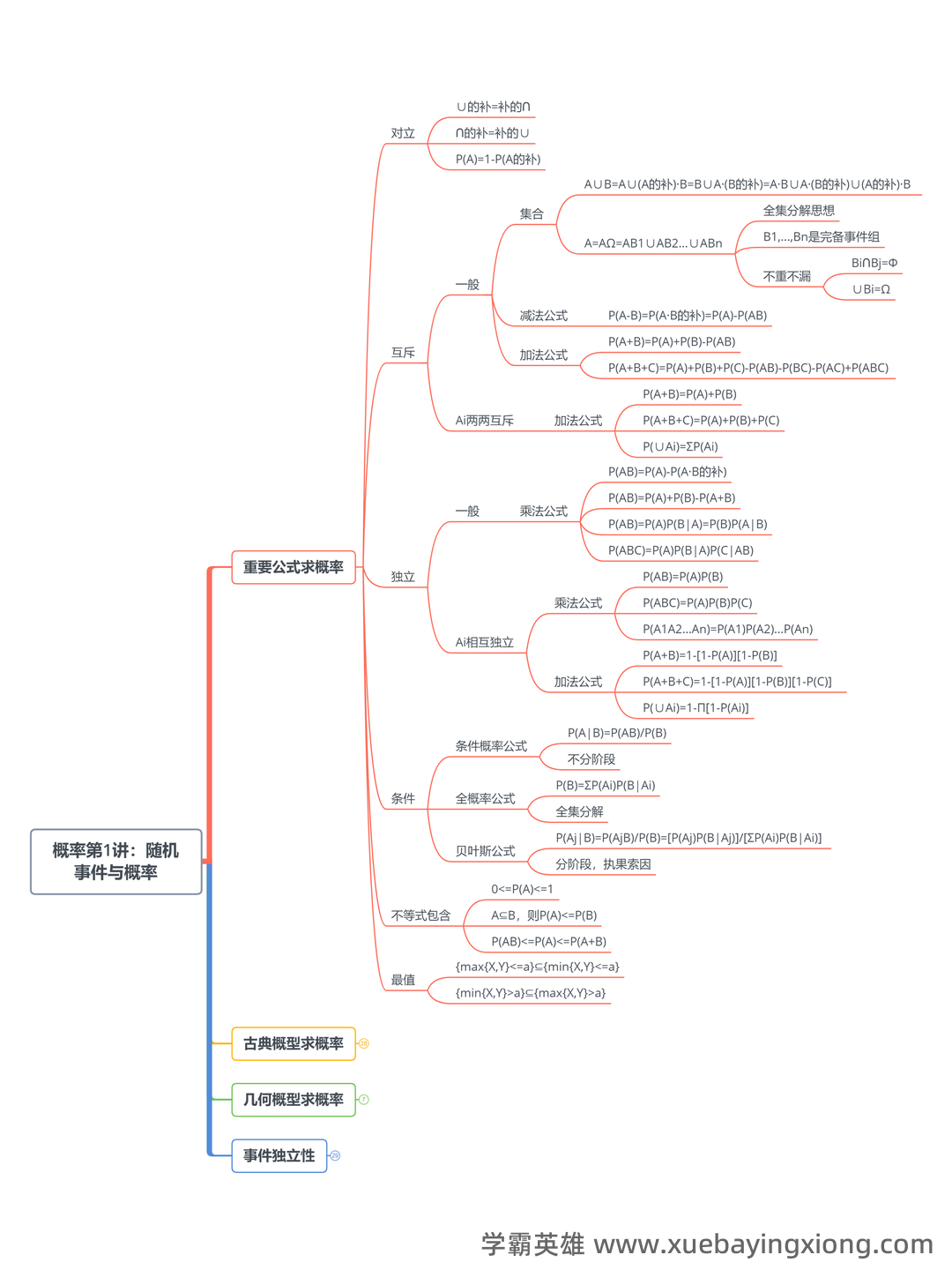
【概率论与数理统计】1.5 独立性_概率论与数理统计名词解释
【概率论与数理统计】1.5 独立性_概率论与数理统计名词解释 在概率论的广阔天地里，“独立性”是一个至关重要的概念。简单来说，如果两个事件是独立的，意味着一个事件的发生对另一个事件的发生没有任何影响。换句话说，我们无法通过已知一个事件是否发生来预测另一个事件的发生概率。 严格来说，概率论中的“独立性”指的是在给定条件下，事件发生的概率与其它条件事件发生的概率无关。 为了更清晰地理解这个概念，我们回到概率论的定义——概率是衡量随机事件发生几率的量度。 如果两个事件A和B是独立的，那么P(A∩B) = P(A) P(B)，即事件A和B同时发生的概率等于它们各自发生的概率的乘积。 这种乘积关系是概率论中描述独立事件的关键。 举个例子，假设你扔硬币，正面朝上的概率是50%。如果事件“第一次扔硬币正面朝上”和“第二次扔硬币正面朝上”是独立的，那么第二次正面朝上的概率仍然是50%，与第一次的结果无关。 但如果硬币是“双面都是正面”的，那么这两个事件就不再独立，因为第二次正面朝上的概率会受到第一次结果的影响。 理解独立性对于许多领域都非常重要。在金融领域，独立性可以用来评估投资组合的风险；在医学领域，它可以用来分析疾病的发生与某些因素之间的关系。 掌握独立性这一核心概念，是深入学习概率论和数理统计的基础。 无论是在理论研究还是实际应用中，理解独立性都能帮助我们更准确地认识和分析世界。
展开
概率论
2025-07-22
13次阅读