第 1 页 / 共 34 页
第 2 页 / 共 34 页
第 3 页 / 共 34 页
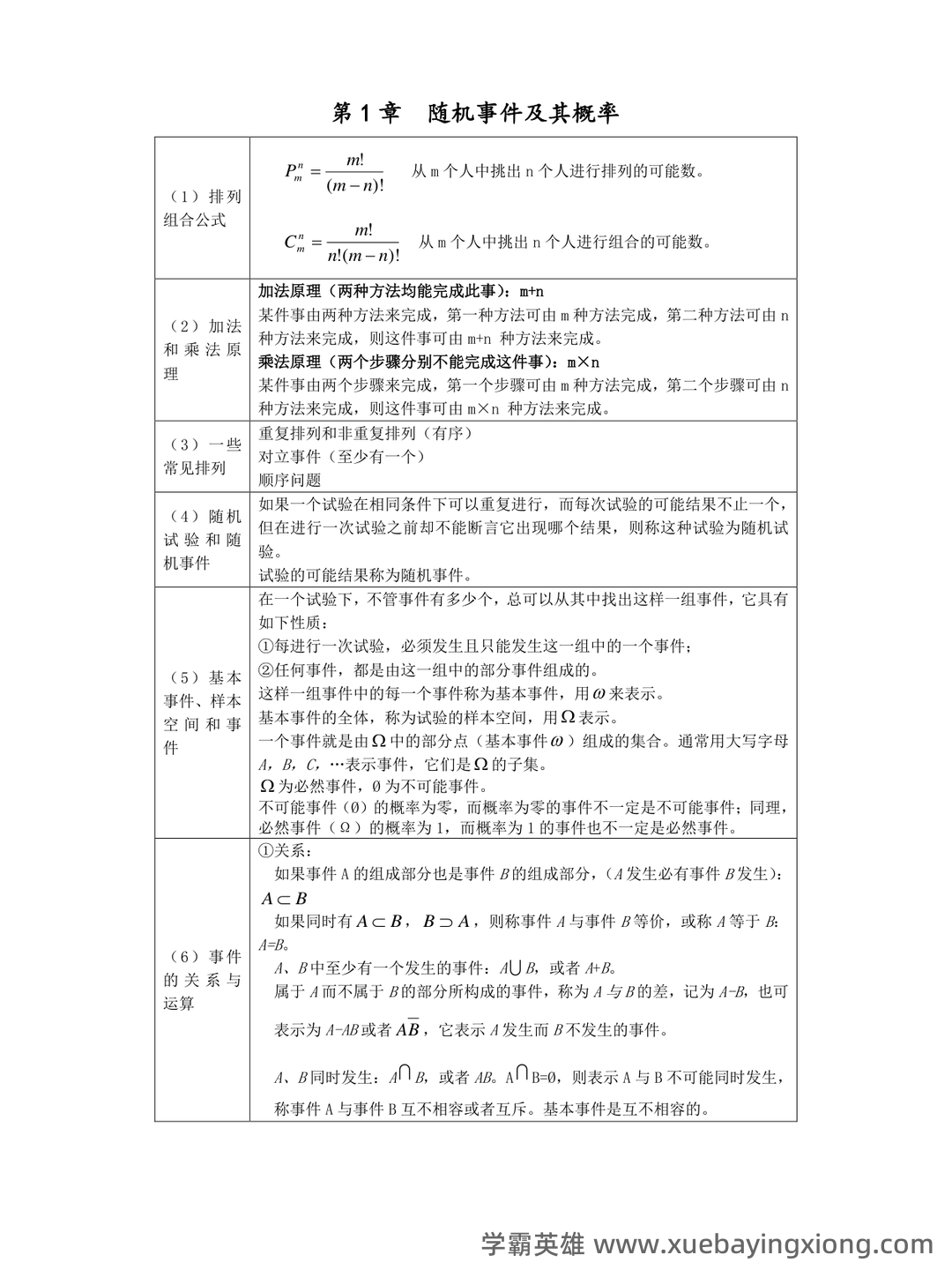
第 4 页 / 共 34 页
第 5 页 / 共 34 页
第 6 页 / 共 34 页
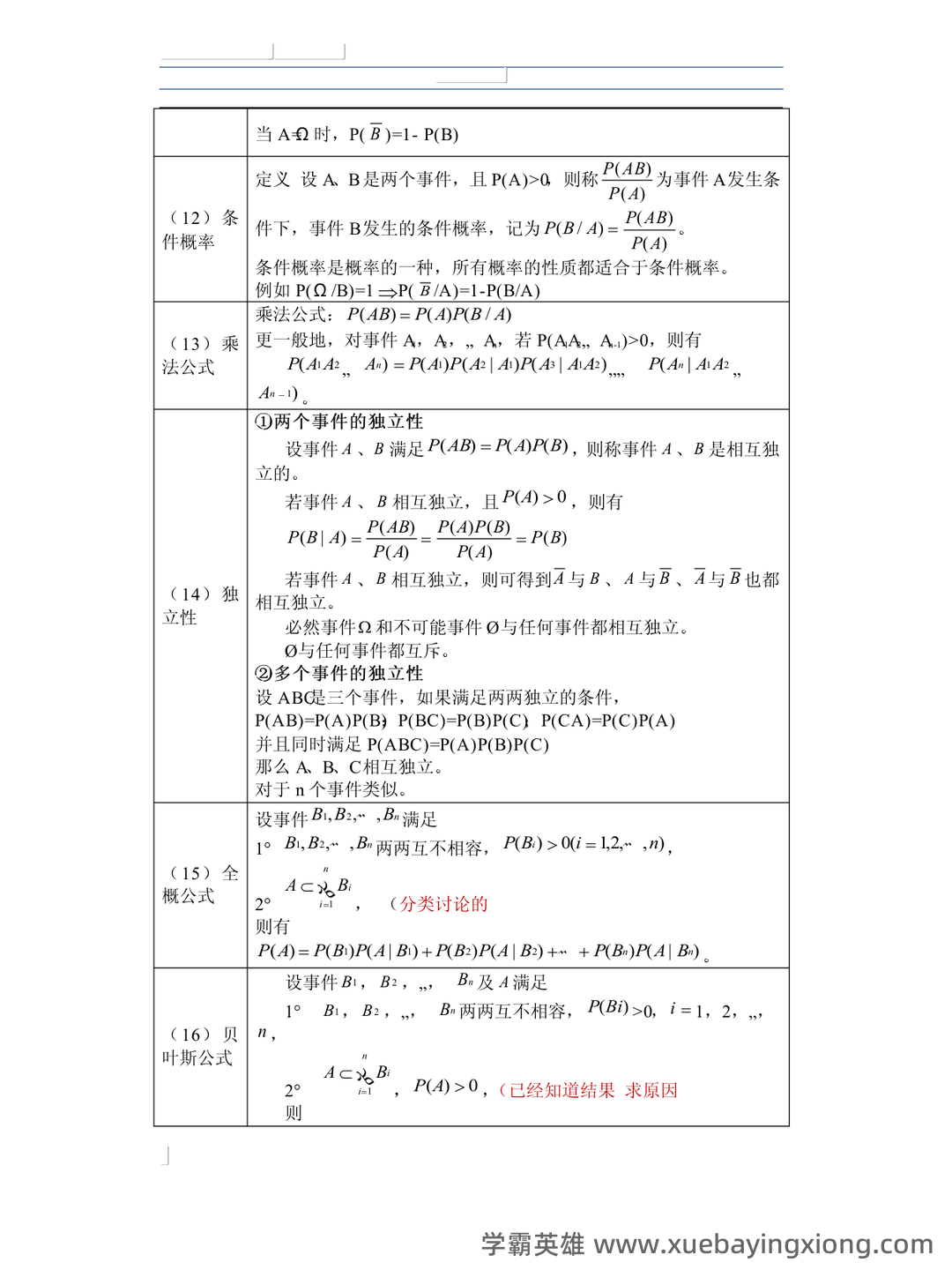
第 7 页 / 共 34 页
第 8 页 / 共 34 页
第 9 页 / 共 34 页
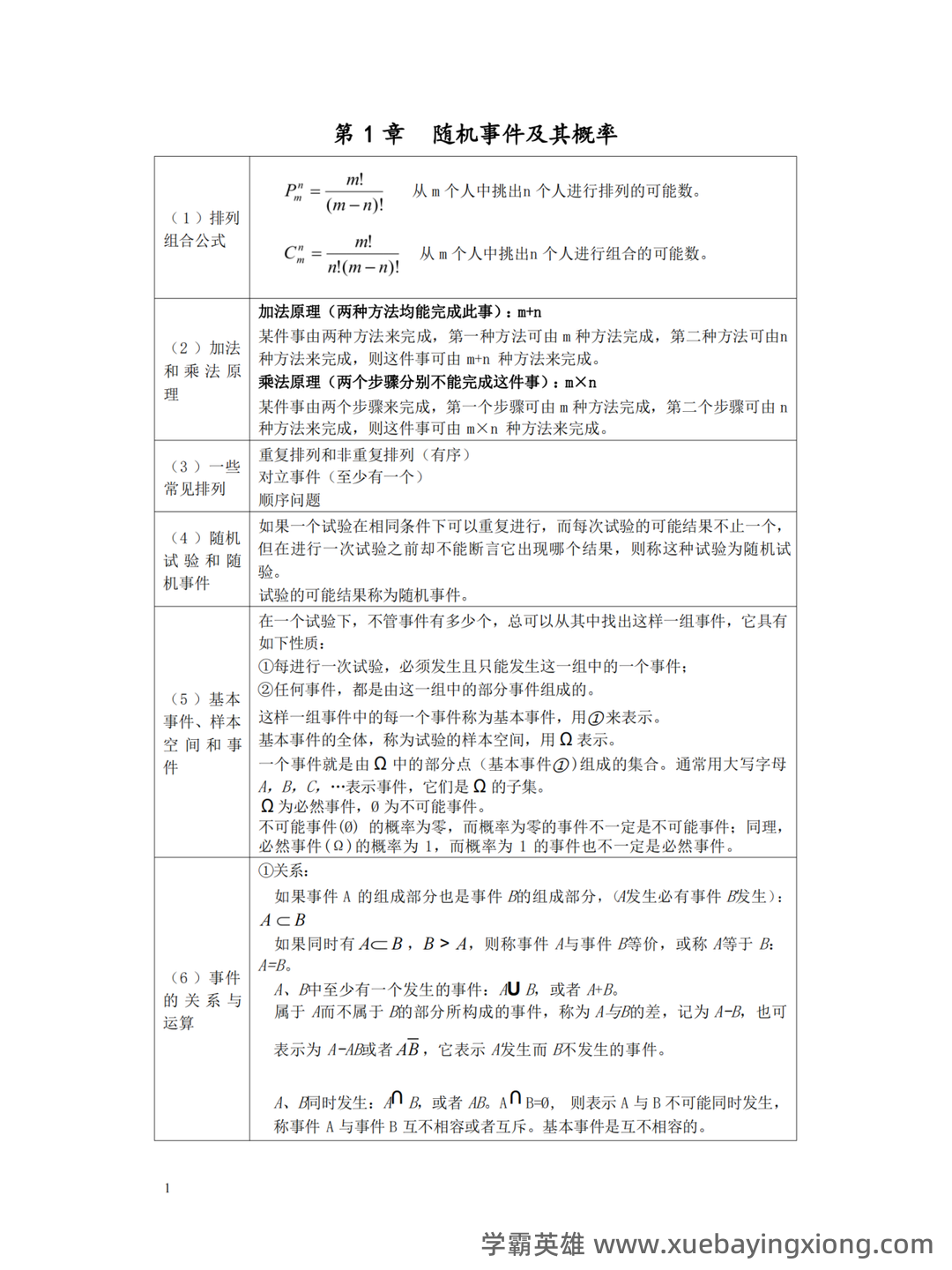
第 10 页 / 共 34 页
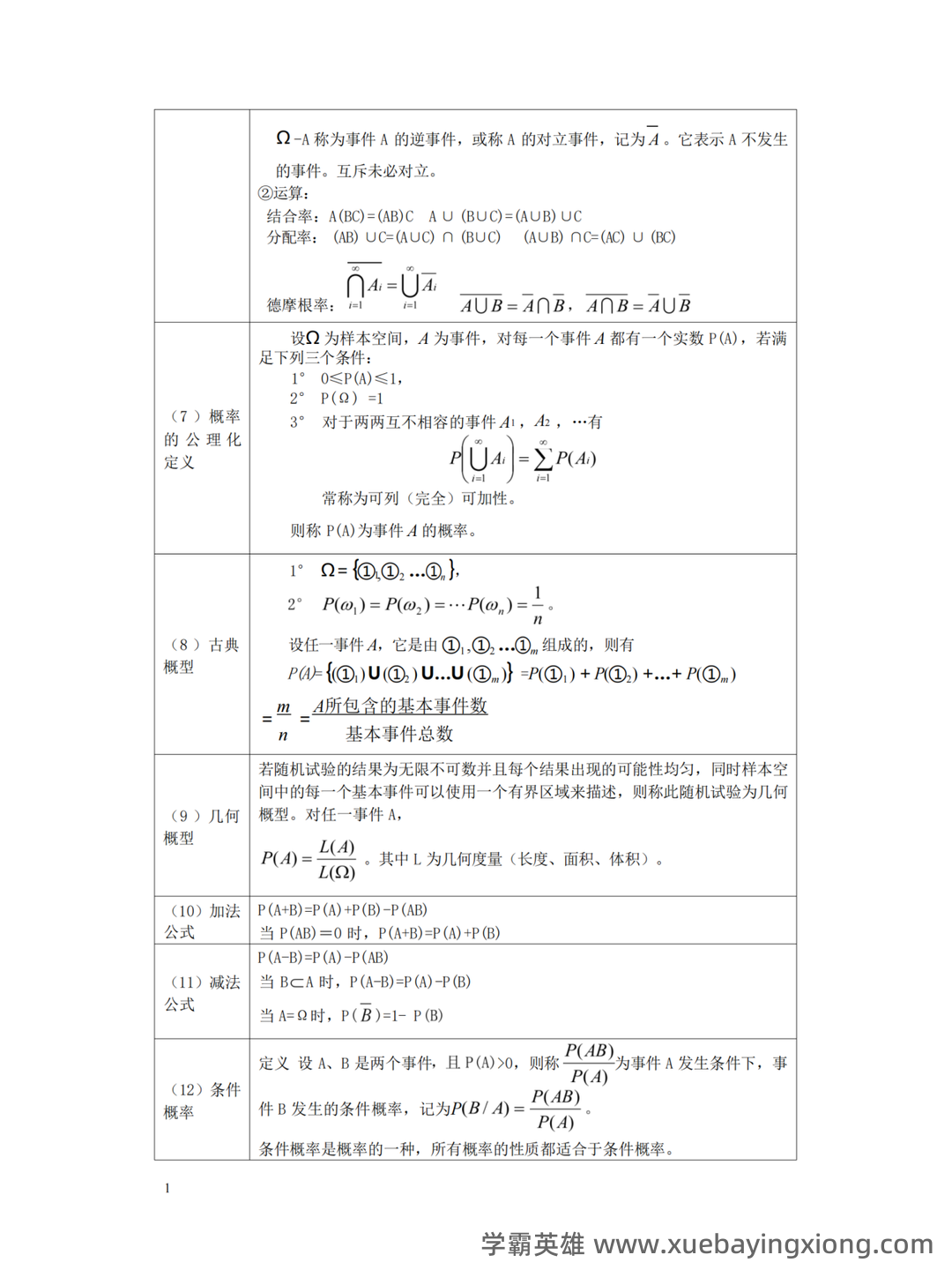
第 11 页 / 共 34 页
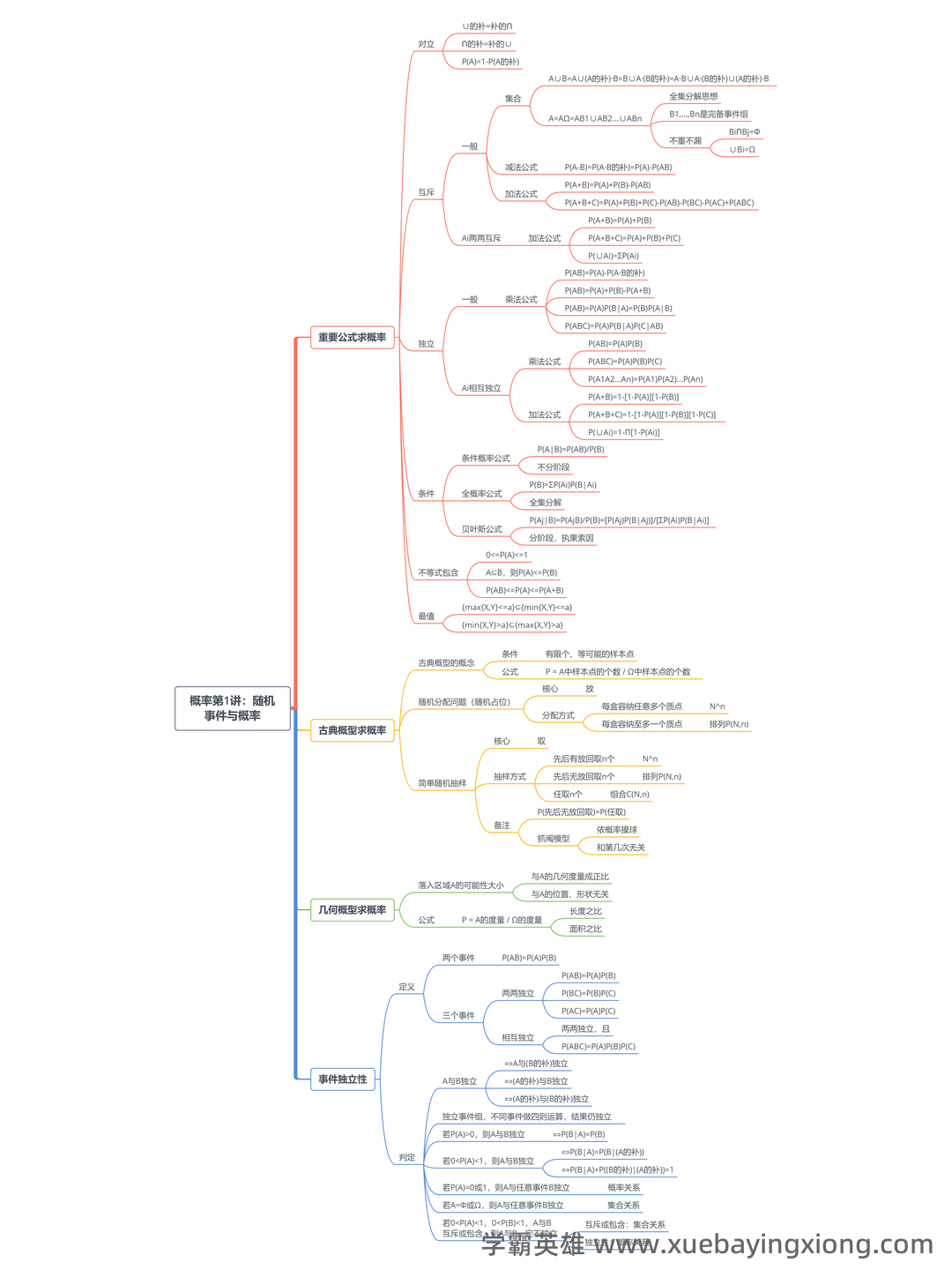
第 12 页 / 共 34 页
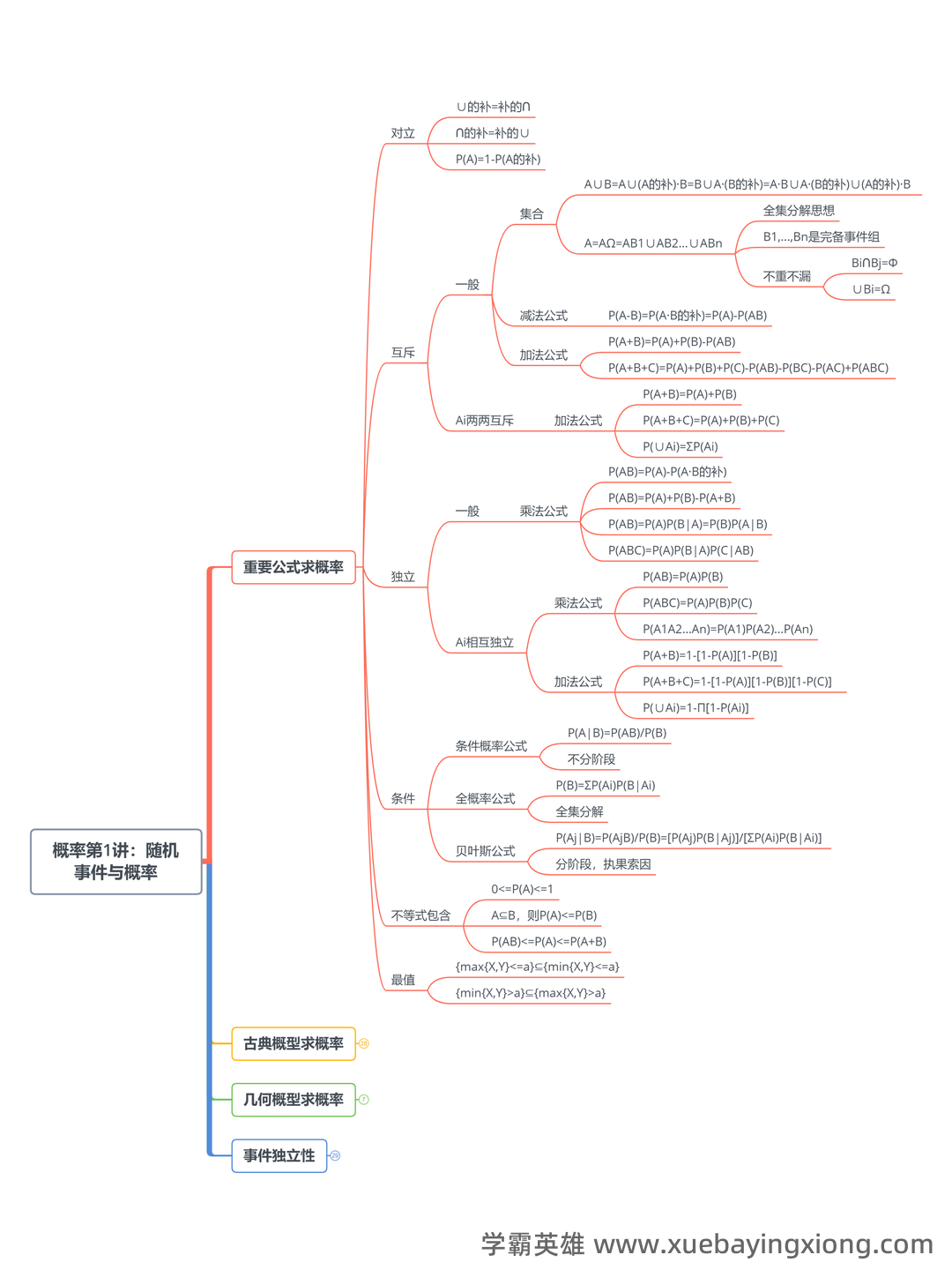
第 13 页 / 共 34 页
第 14 页 / 共 34 页
第 15 页 / 共 34 页
第 16 页 / 共 34 页
第 17 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论名词简短解释 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 18 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论名词简短解释 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 19 页 / 共 34 页
第 20 页 / 共 34 页
第 21 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论名词简短解释 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 22 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论名词简短解释 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 23 页 / 共 34 页
第 24 页 / 共 34 页
第 25 页 / 共 34 页
第 26 页 / 共 34 页
第 27 页 / 共 34 页
第 28 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论名词简短解释 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 29 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论名词简短解释 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 30 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论名词简短解释 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 31 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论名词简短解释 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 32 页 / 共 34 页
第 33 页 / 共 34 页
第 34 页 / 共 34 页
概率论名词简短解释
概率论名词简短解释 概率论，听起来好像很高深，其实它根植于我们日常生活中的无数选择。简单来说，它就是研究随机事件的可能性，以及这些可能性是如何相互关联的。它不是预测未来，而是帮助我们理解不确定性。 在概率论中，我们经常会遇到“概率”这个概念。概率就是指一个事件发生的可能性大小，通常用0到1之间的数字表示。0代表不可能发生，1代表必然发生。例如，抛硬币，正面朝上的概率是1/2，反面朝上的概率也是1/2。 更深层次的概率论涉及到“样本空间”和“事件”。 样本空间是指所有可能结果的集合，而事件是指样本空间中的一个或多个结果。 比如，掷骰子的样本空间包括1到6的数字，如果事件是“掷出3”，那么这个事件就是样本空间中的一个子集。 “条件概率”是概率论中一个重要的概念。它指的是在已知某个事件已经发生的情况下，另一个事件发生的概率。 举个例子，如果知道某位病人已经感染了某种疾病，那么他再次感染的概率会比没有被感染的概率更高。 “贝叶斯定理”则提供了一种更新概率的方法。它允许我们根据新的证据来修正对事件发生的概率的估计。 这在很多领域都有广泛的应用，比如医学诊断、金融建模等等。 总而言之，概率论提供了一个强大的工具，帮助我们分析和理解各种不确定性。 它不仅仅是数学，更是一种思考方式，一种处理复杂问题的武器。
展开
概率论
2025-07-22
12次阅读