第 1 页 / 共 34 页
第 2 页 / 共 34 页
第 3 页 / 共 34 页
第 4 页 / 共 34 页
第 5 页 / 共 34 页
第 6 页 / 共 34 页
第 7 页 / 共 34 页
第 8 页 / 共 34 页
第 9 页 / 共 34 页
第 10 页 / 共 34 页
第 11 页 / 共 34 页
第 12 页 / 共 34 页
第 13 页 / 共 34 页
第 14 页 / 共 34 页
第 15 页 / 共 34 页
第 16 页 / 共 34 页
第 17 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计基础概念与重要定义汇总_概率论及数理统计概念 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 18 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计基础概念与重要定义汇总_概率论及数理统计概念 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 19 页 / 共 34 页
第 20 页 / 共 34 页
第 21 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计基础概念与重要定义汇总_概率论及数理统计概念 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 22 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计基础概念与重要定义汇总_概率论及数理统计概念 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 23 页 / 共 34 页
第 24 页 / 共 34 页
第 25 页 / 共 34 页
第 26 页 / 共 34 页
第 27 页 / 共 34 页
第 28 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计基础概念与重要定义汇总_概率论及数理统计概念 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 29 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计基础概念与重要定义汇总_概率论及数理统计概念 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 30 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计基础概念与重要定义汇总_概率论及数理统计概念 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 31 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计基础概念与重要定义汇总_概率论及数理统计概念 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 32 页 / 共 34 页
第 33 页 / 共 34 页
第 34 页 / 共 34 页
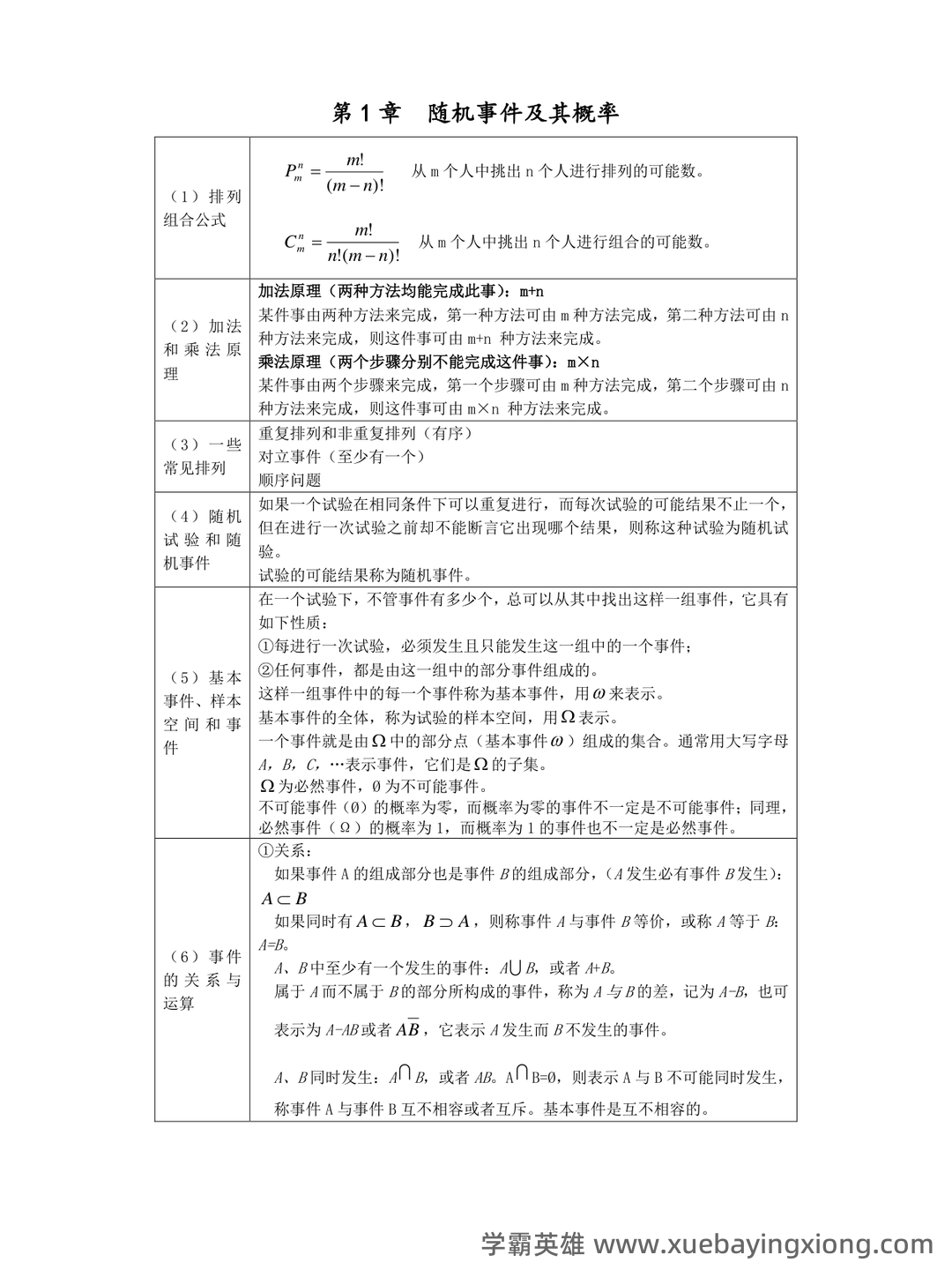
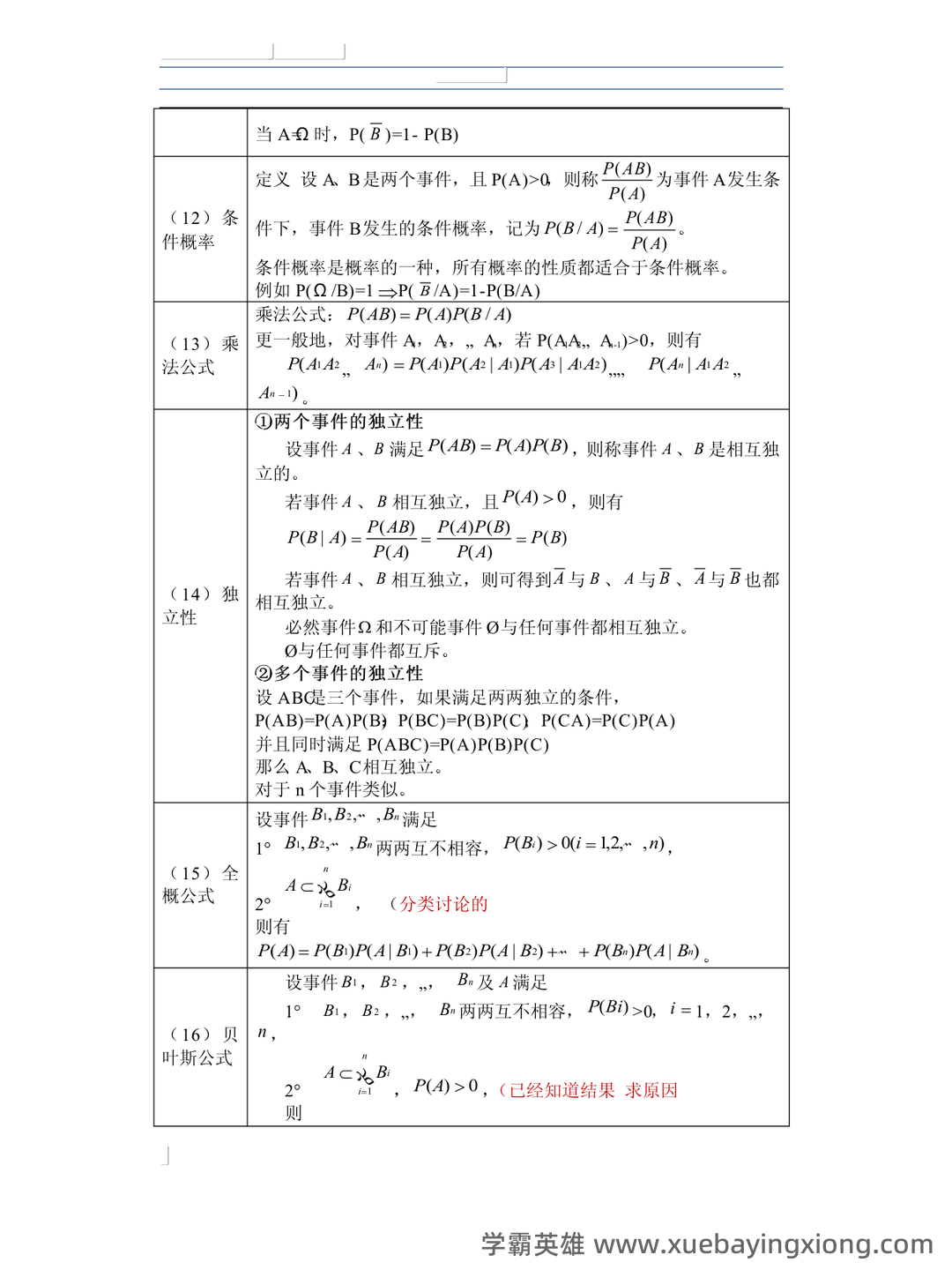
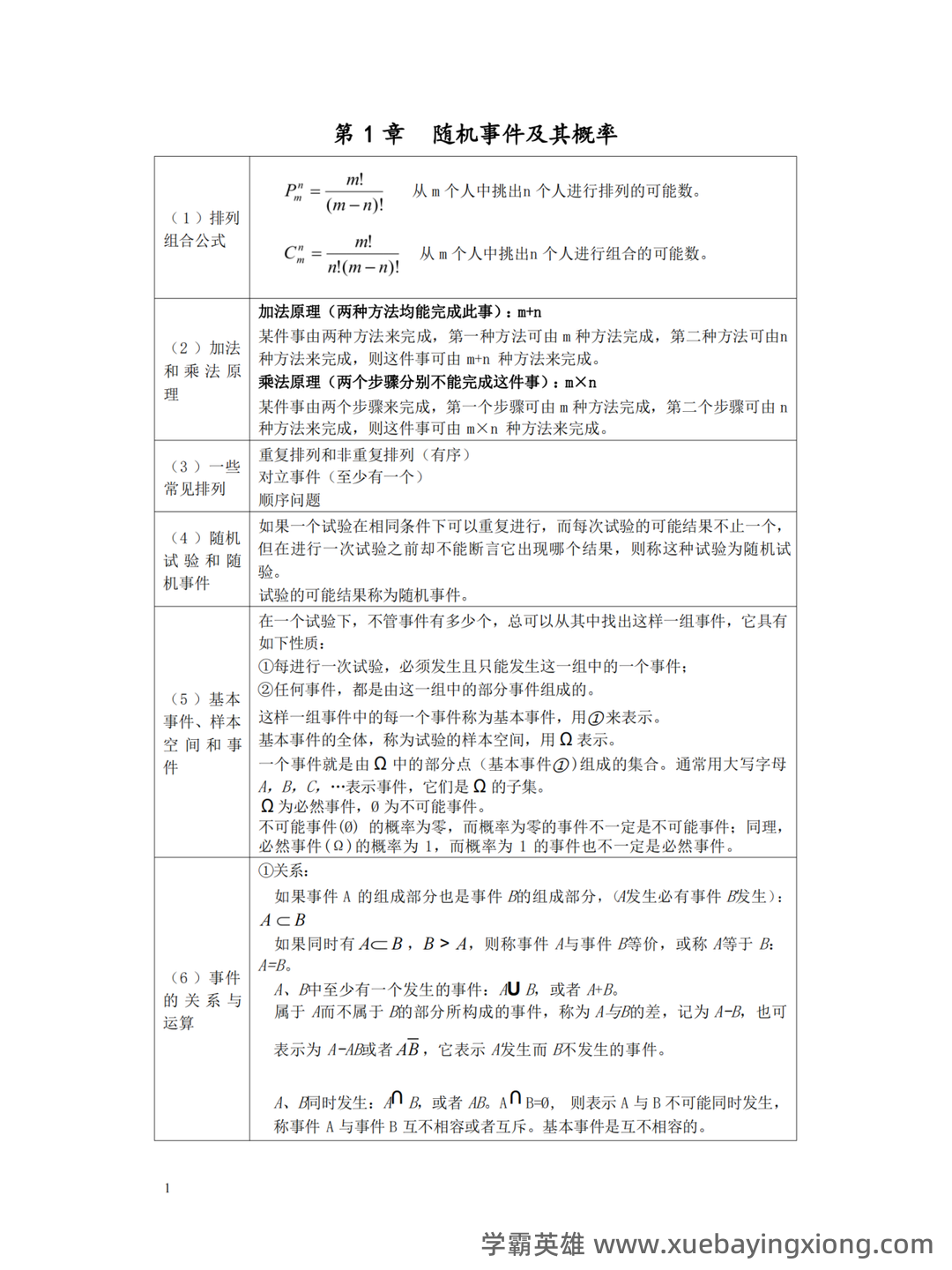
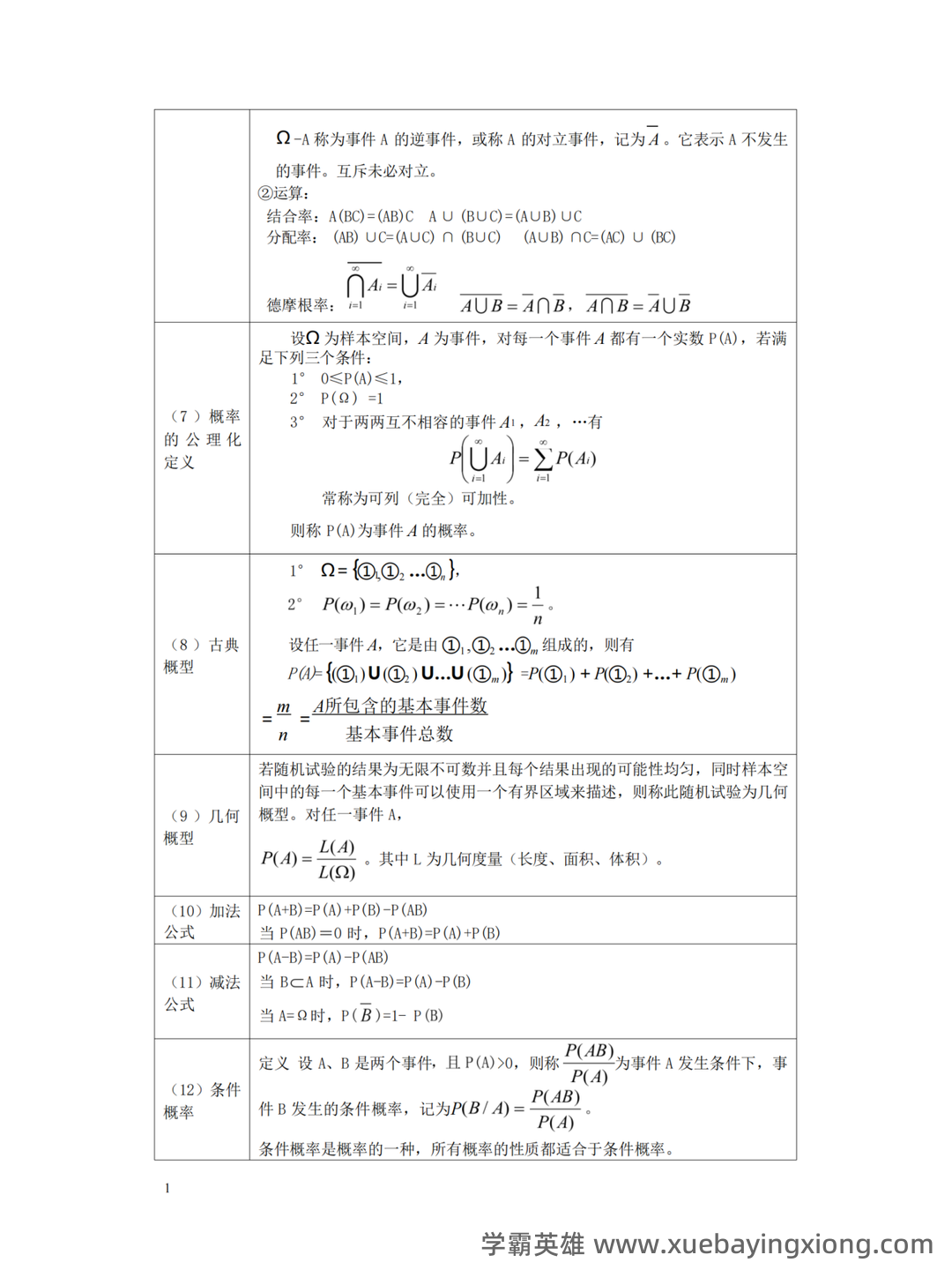
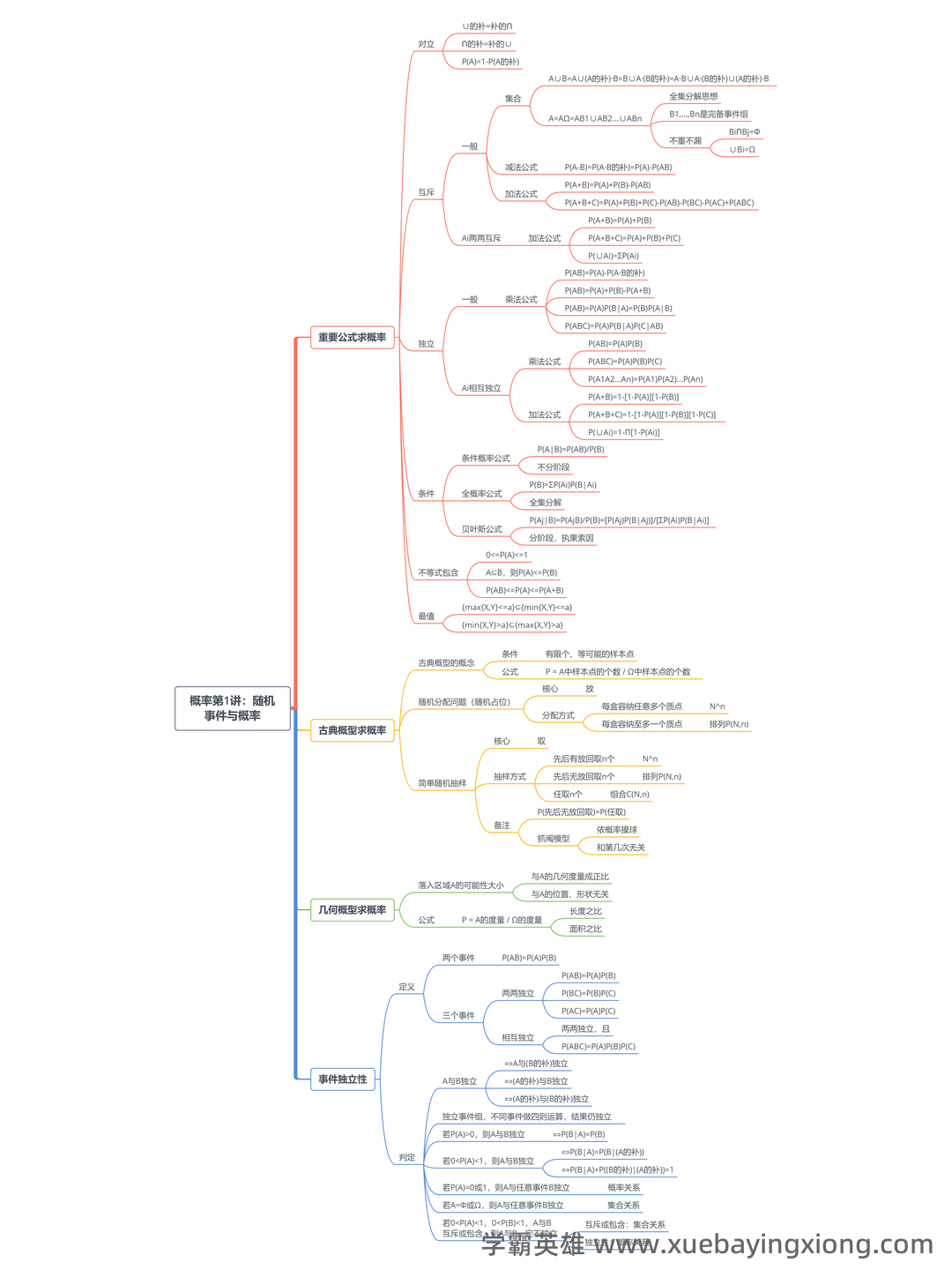
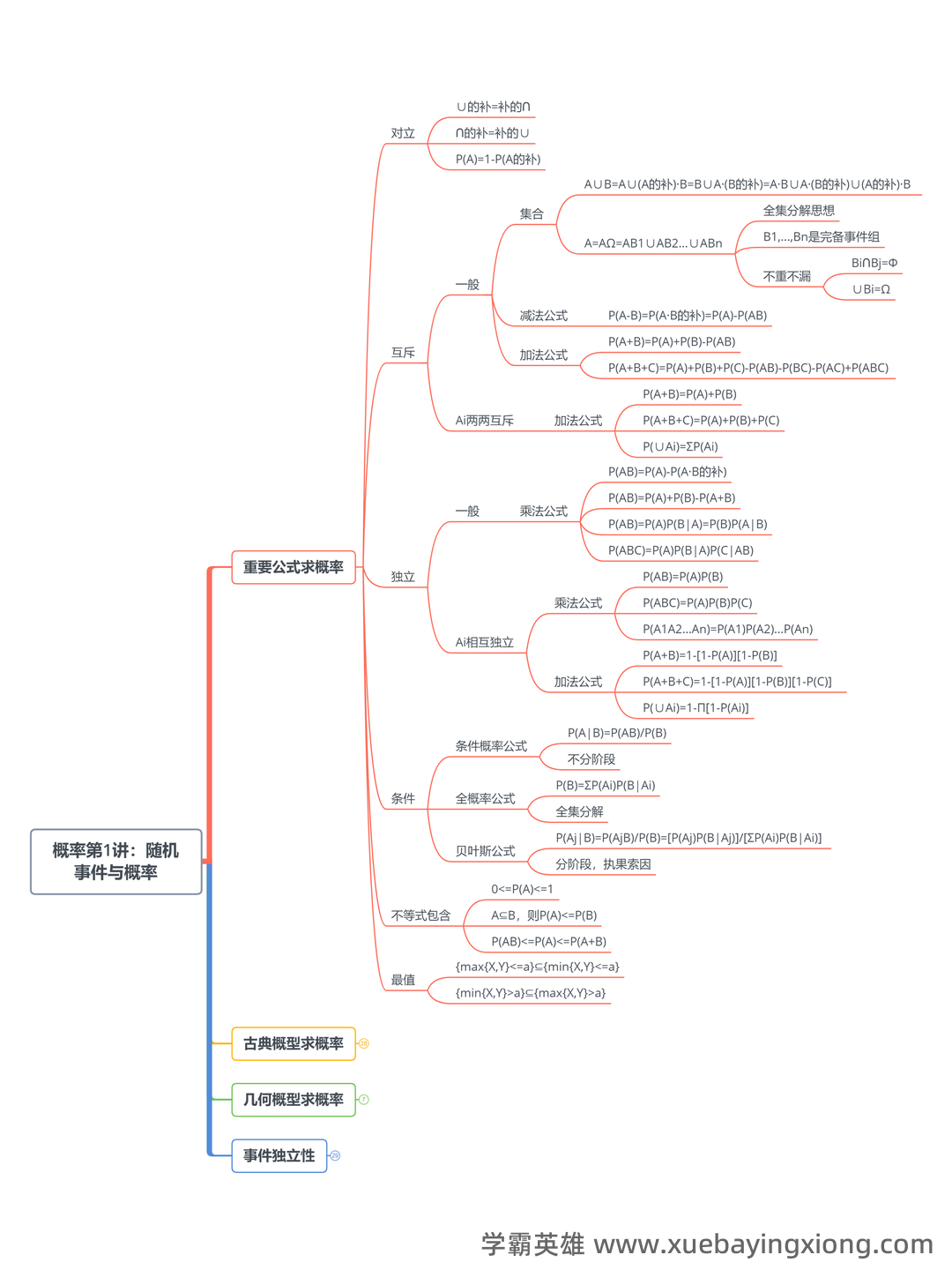
概率论与数理统计基础概念与重要定义汇总_概率论及数理统计概念
概率论与数理统计，这两个看似关联紧密的名词，实则构建了现代数据分析和建模的基石。简单来说，概率论是研究随机现象及其规律的数学分支，它赋予了我们评估不确定性、预测未来趋势的能力。在概率论中，核心概念包括样本空间、事件、概率等。理解“概率”本身就至关重要：它代表一个事件发生的可能性大小，范围从0（不可能）到1（必然）。 数理统计则是在概率论的基础上，专门研究如何从数据中提取信息、建立模型并进行预测。它关注的是如何用统计方法来分析和解释数据。数理统计的关键概念包括总体、样本、参数、统计量。例如，我们通过样本的平均值来估计总体平均值，这便是统计推断的核心。 在概率论中，常见的概率分布是关键。例如，正态分布、二项分布、泊松分布等等，每种分布都对应着不同的现象和应用场景。理解这些分布的特性，能够帮助我们更好地理解数据的分布情况，并进行更准确的分析和预测。 数理统计中，重要的定义包括但不限于：期望值、方差、标准差。期望值衡量的是一个随机变量的平均值，方差和标准差则反映了数据的离散程度。 掌握这些基本概念，对于进行统计分析和建模至关重要。 总而言之，概率论和数理统计是紧密相连的，它们提供了理解和处理不确定性、分析数据、建立模型以及进行预测的强大工具。 掌握这门学科，就是掌握了一种解决问题、探索世界的钥匙。
展开
概率论
2025-07-22
8次阅读