第 1 页 / 共 34 页
第 2 页 / 共 34 页
第 3 页 / 共 34 页
第 4 页 / 共 34 页
第 5 页 / 共 34 页
第 6 页 / 共 34 页
第 7 页 / 共 34 页
第 8 页 / 共 34 页
第 9 页 / 共 34 页
第 10 页 / 共 34 页
第 11 页 / 共 34 页
第 12 页 / 共 34 页
第 13 页 / 共 34 页
第 14 页 / 共 34 页
第 15 页 / 共 34 页
第 16 页 / 共 34 页
第 17 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计公式大总结（最全） - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 18 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计公式大总结（最全） - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 19 页 / 共 34 页
第 20 页 / 共 34 页
第 21 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计公式大总结（最全） - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 22 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计公式大总结（最全） - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 23 页 / 共 34 页
第 24 页 / 共 34 页
第 25 页 / 共 34 页
第 26 页 / 共 34 页
第 27 页 / 共 34 页
第 28 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计公式大总结（最全） - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 29 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计公式大总结（最全） - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 30 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计公式大总结（最全） - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 31 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "概率论与数理统计公式大总结（最全） - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 32 页 / 共 34 页
第 33 页 / 共 34 页
第 34 页 / 共 34 页
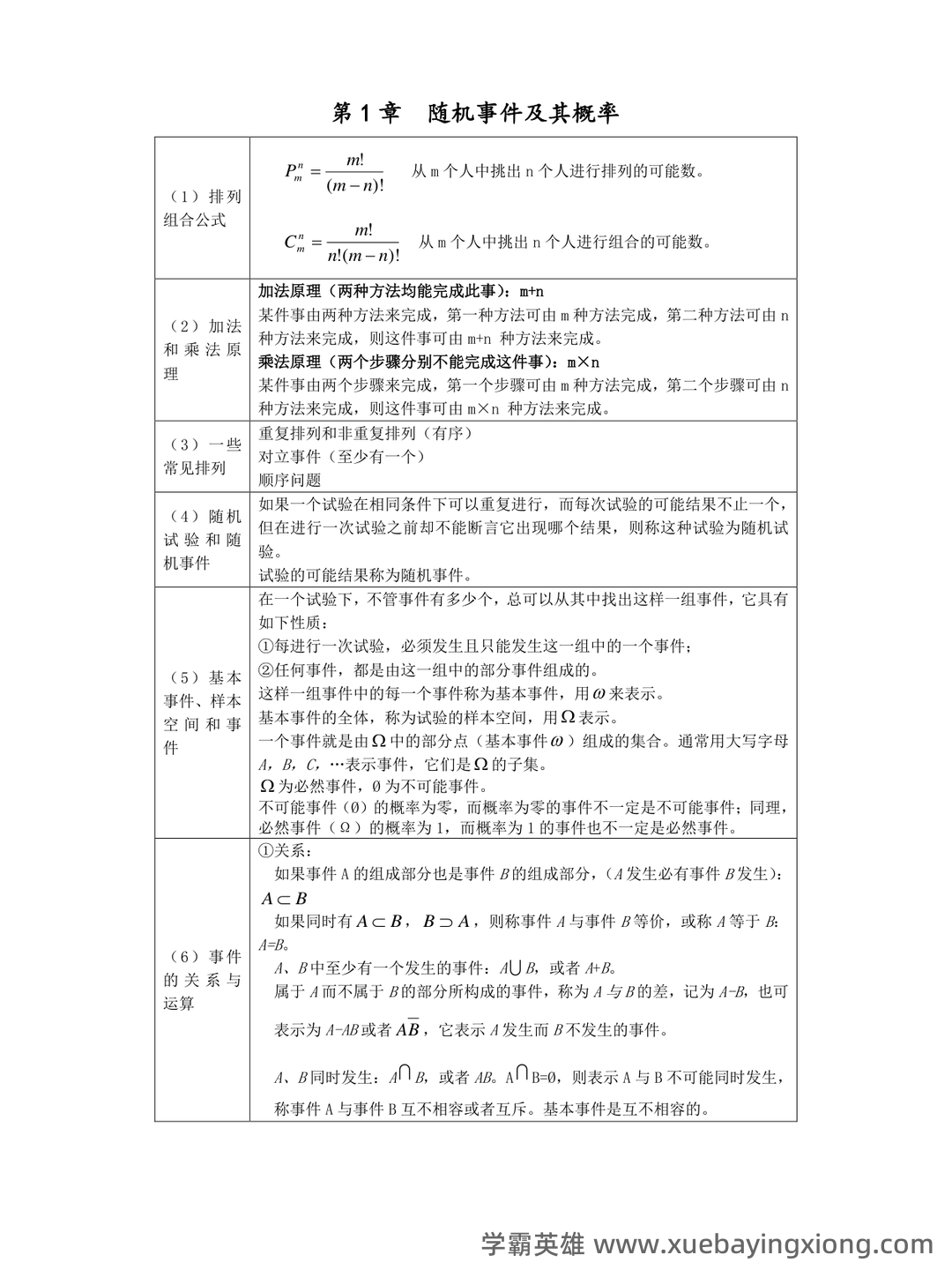
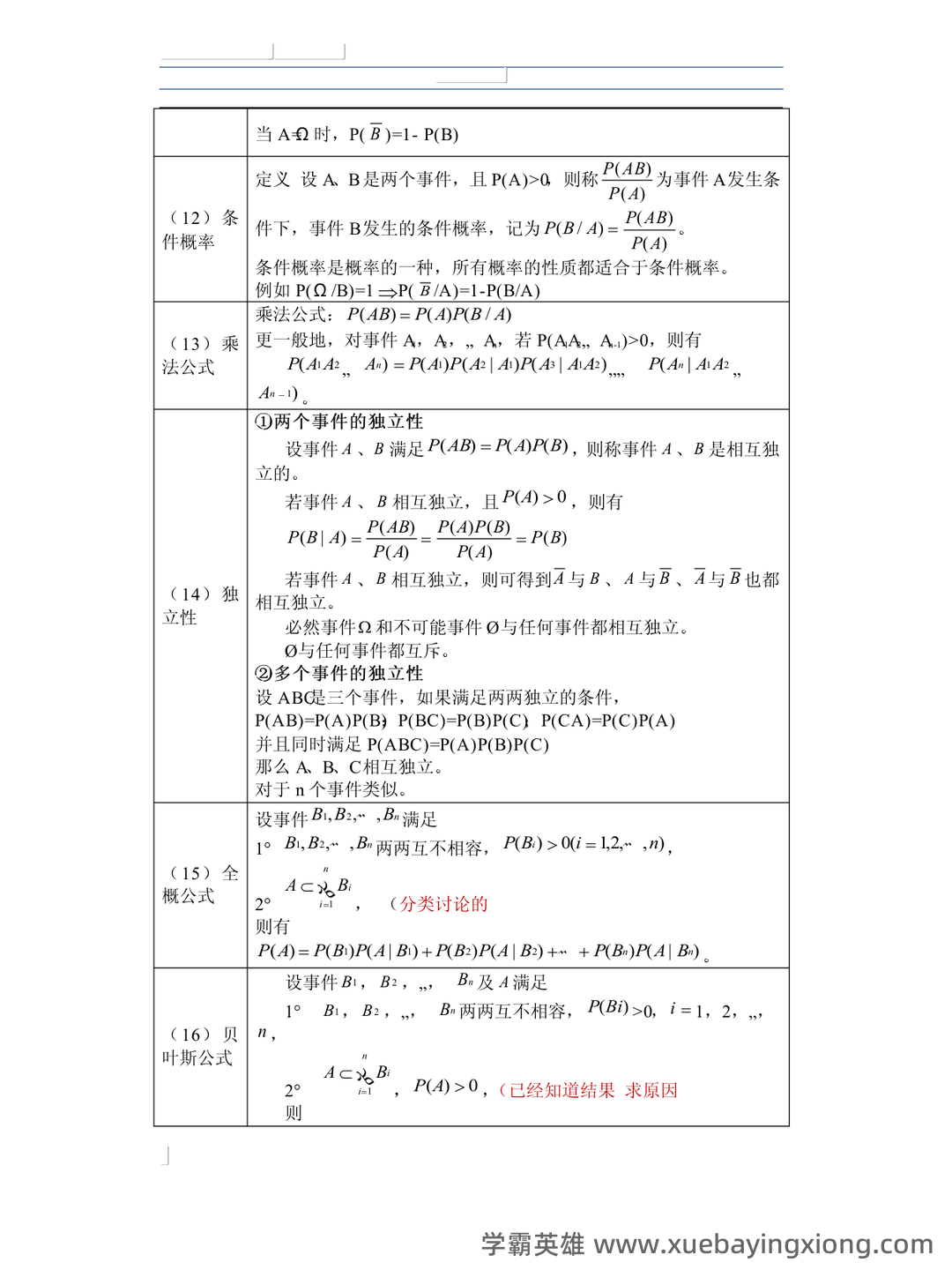
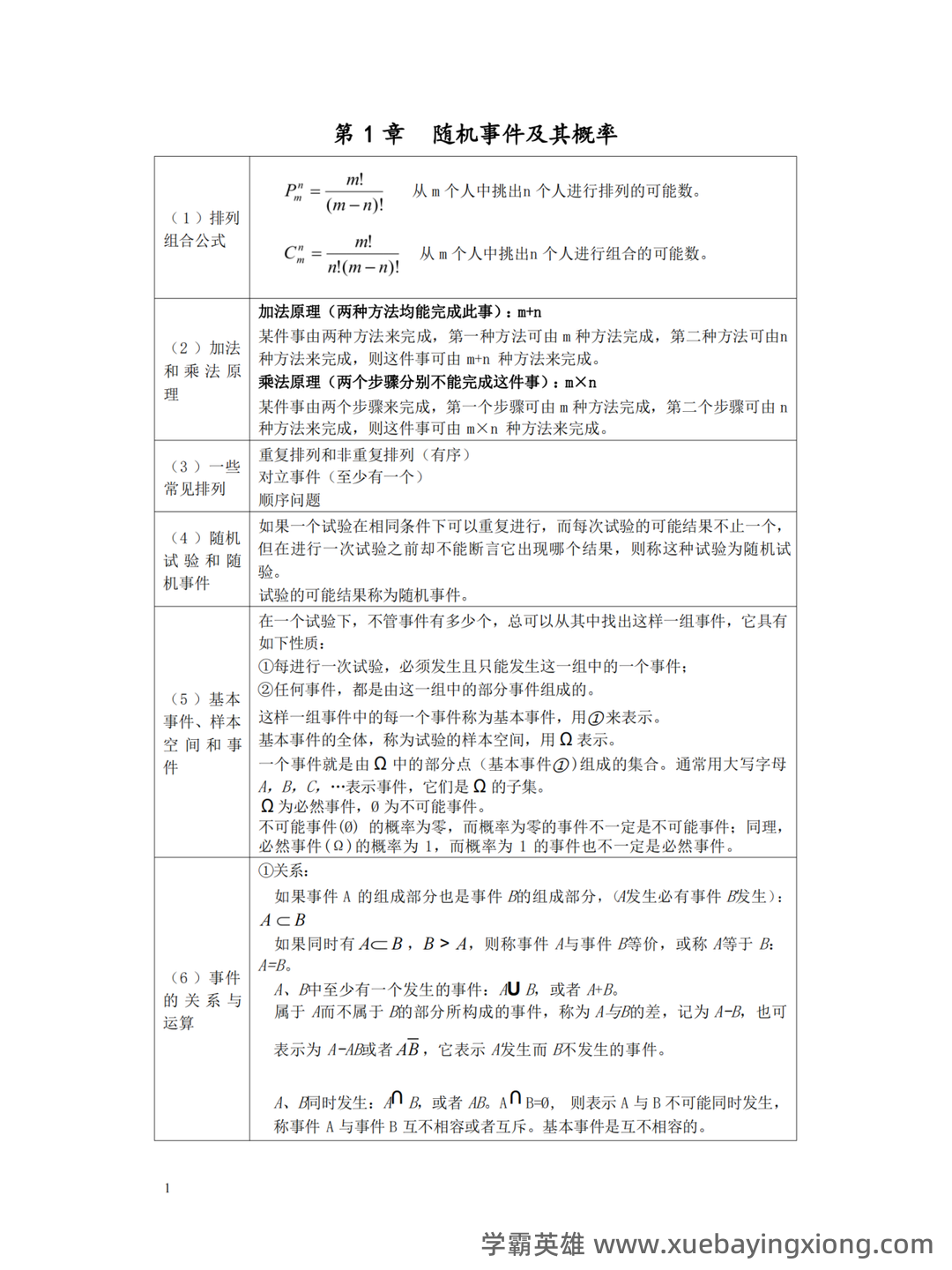
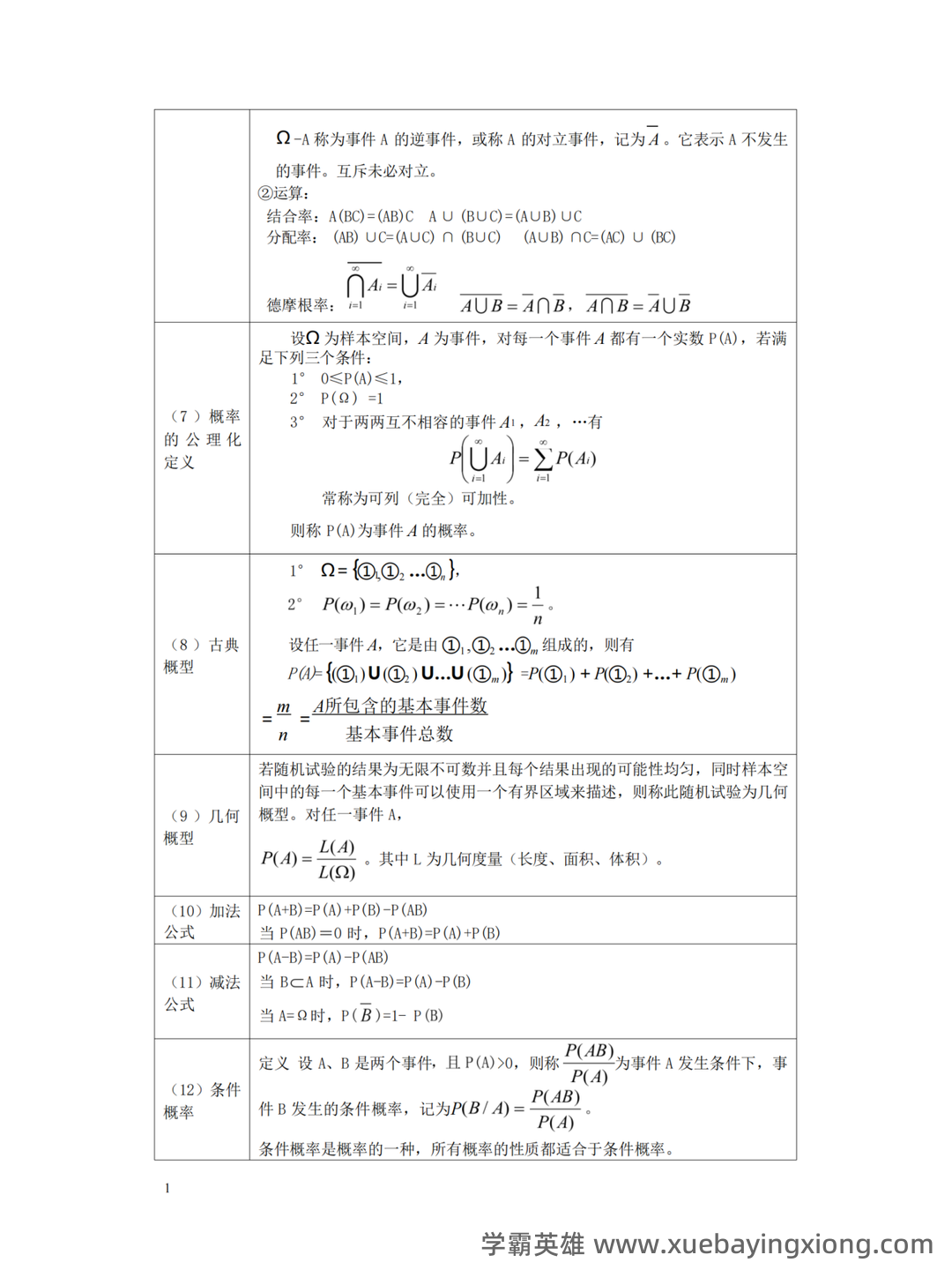
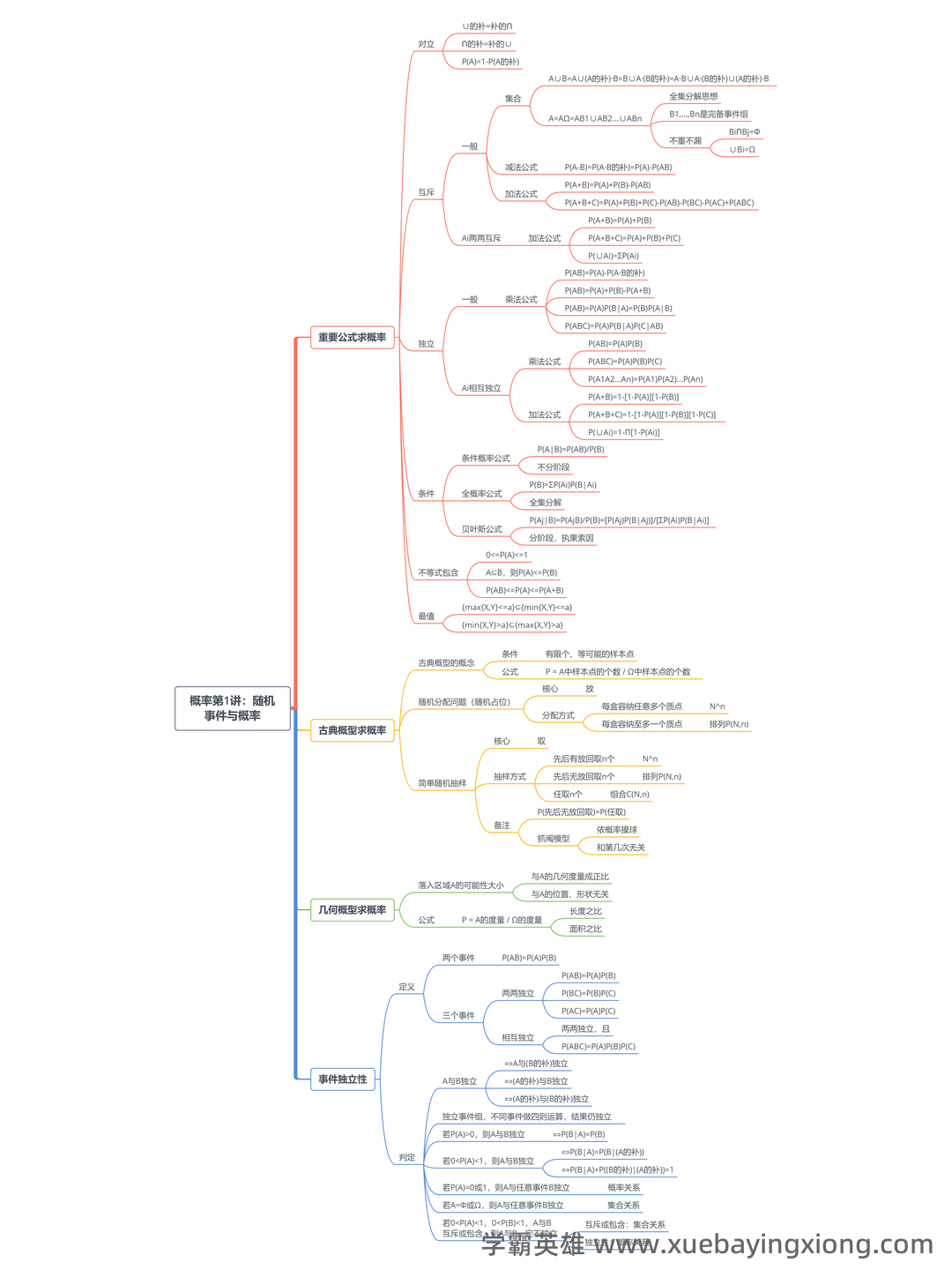
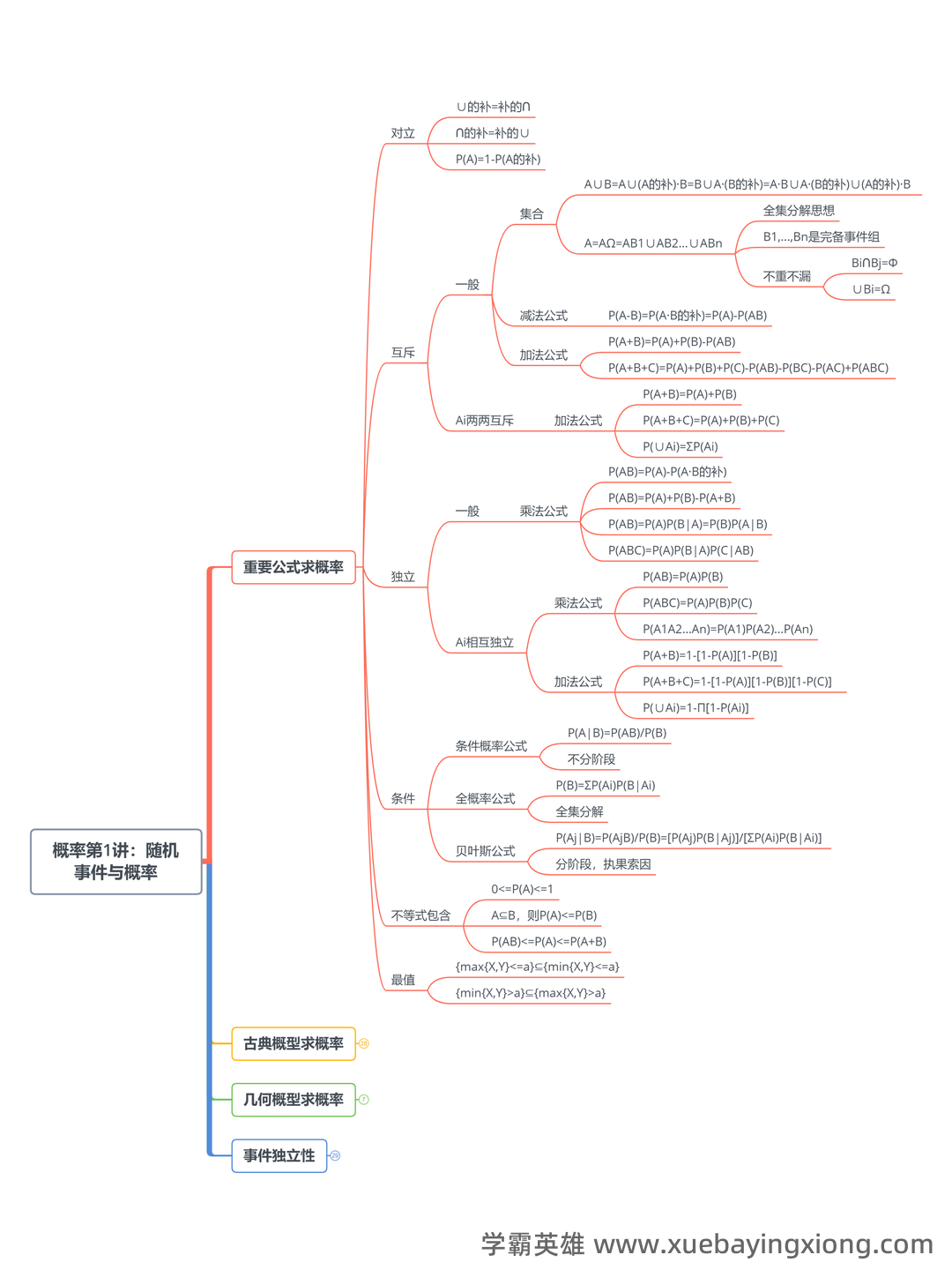
概率论与数理统计公式大总结（最全）
概率论与数理统计公式大总结（最全） 概率论，简单来说，就是研究随机现象规律的数学分支。它提供了一个框架来理解和预测不确定性事件的结果。在统计学中，概率论更是不可或缺的基础，决定了我们如何从数据中提取有意义的信息。理解概率论的关键在于掌握一些核心概念，比如样本空间、事件、概率、条件概率、贝叶斯定理等等。 贝叶斯定理，这个公式简直是概率论的“明星”，它将先验概率和似然度结合起来，给出后验概率的计算方法。公式如下：P(A|B) = [P(B|A) P(A)] / P(B)， 简单来说，就是根据观察到的证据 (B) 来更新我们对事件 A 概率的估计。掌握好这个公式，就如同掌握了一把打开未知世界的大钥匙。 数理统计则利用概率论的结果，来分析数据，得出结论。许多常用的统计公式都直接来源于概率论的原理。例如，均值的计算公式：μ = E(X)， 其中μ代表均值，E(X)代表期望值。 另一个重要的公式是标准差的公式：σ = √[Σ(xi - μ)² / n]， 用来衡量数据的离散程度。 除了上述公式，统计学还涉及到许多其他重要的概念和公式，比如t分布、卡方分布、F分布等等。 熟悉这些公式，并理解它们的应用场景，才能真正掌握概率论和数理统计的精髓。 记住，概率论的核心在于建立模型，预测未来，而数理统计则帮助我们从数据中验证这些模型的有效性。
展开
概率论
2025-07-22
10次阅读