概率论-基础篇笔记(更完)_e(∑xi)=∑(exi)-CSDN - 00_《概率论与数理统计》复习资料_封面首图_学霸英雄_www.xuebayingxiong.com
第 1 页 / 共 34 页
获取资料
学霸英雄

概率论-基础篇笔记(更完)_e(∑xi)=∑(exi)-CSDN

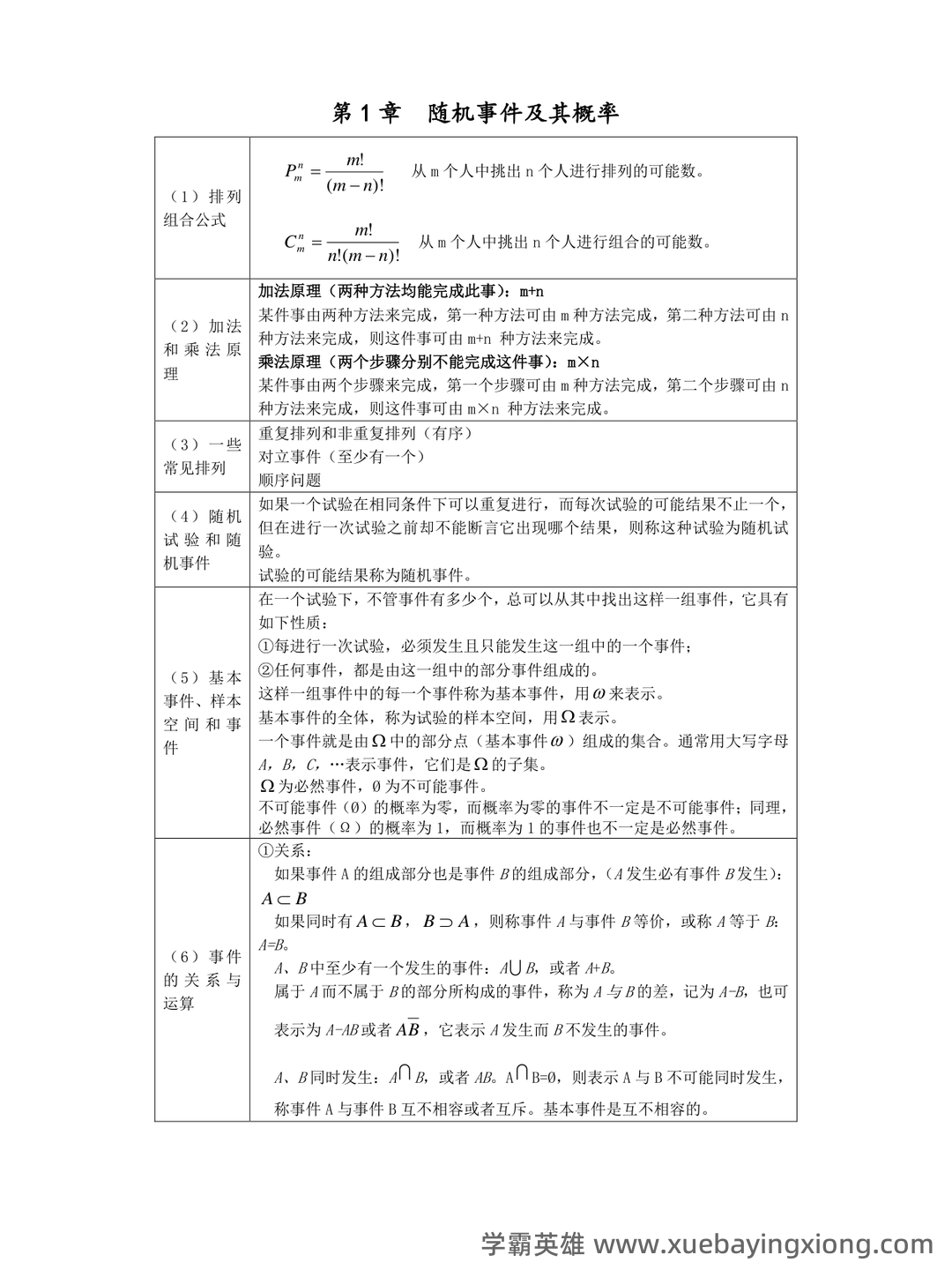
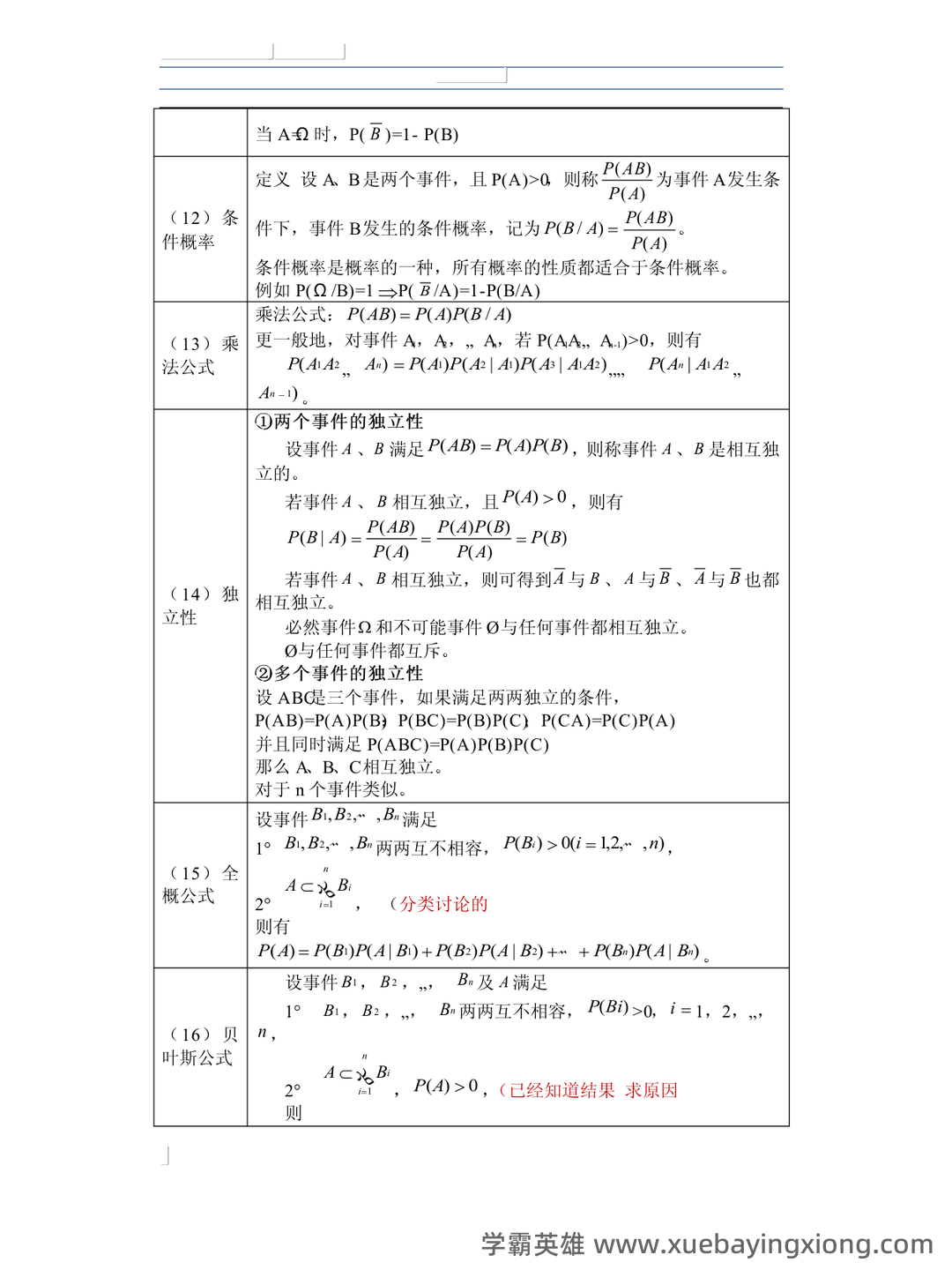
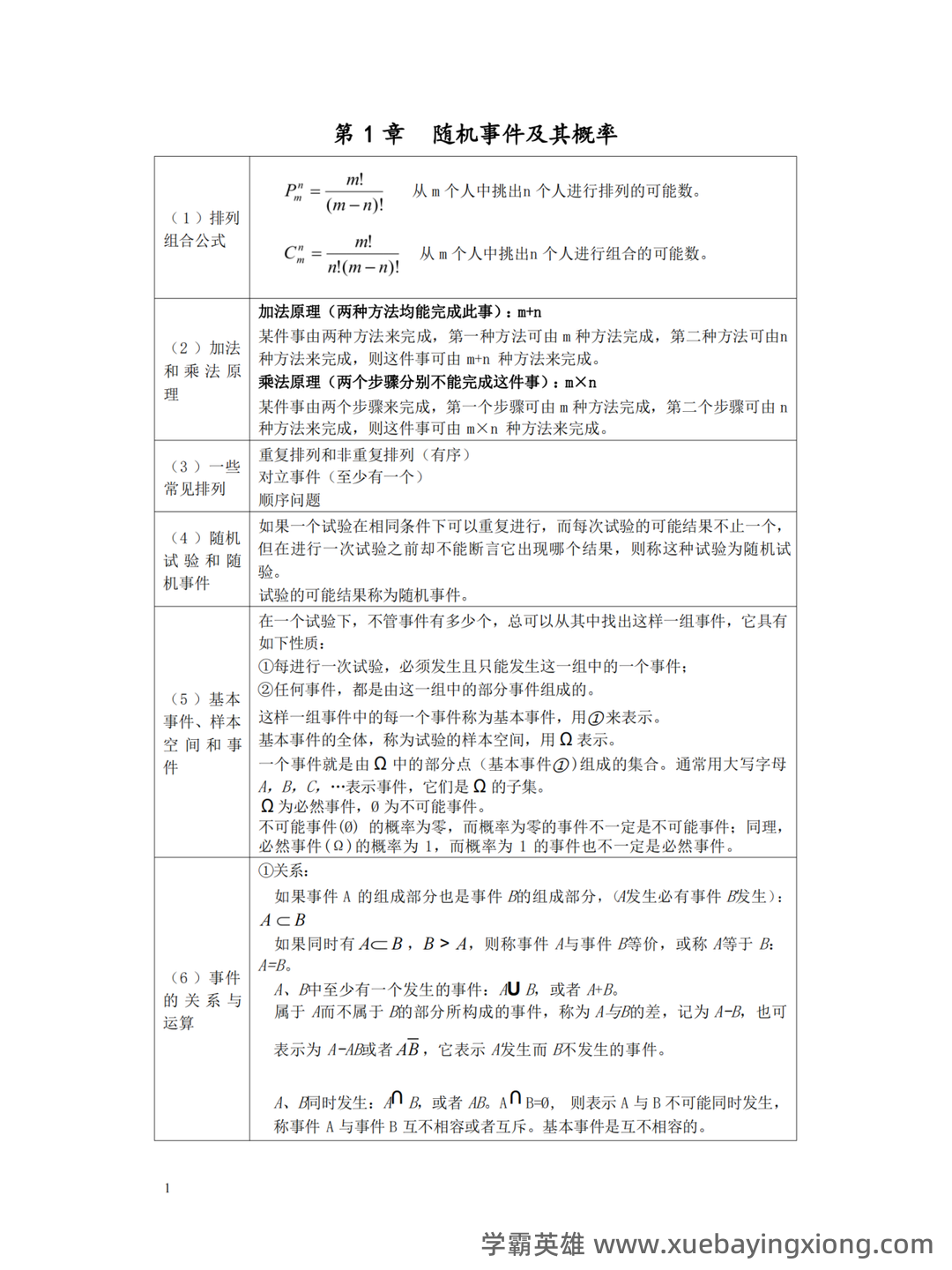
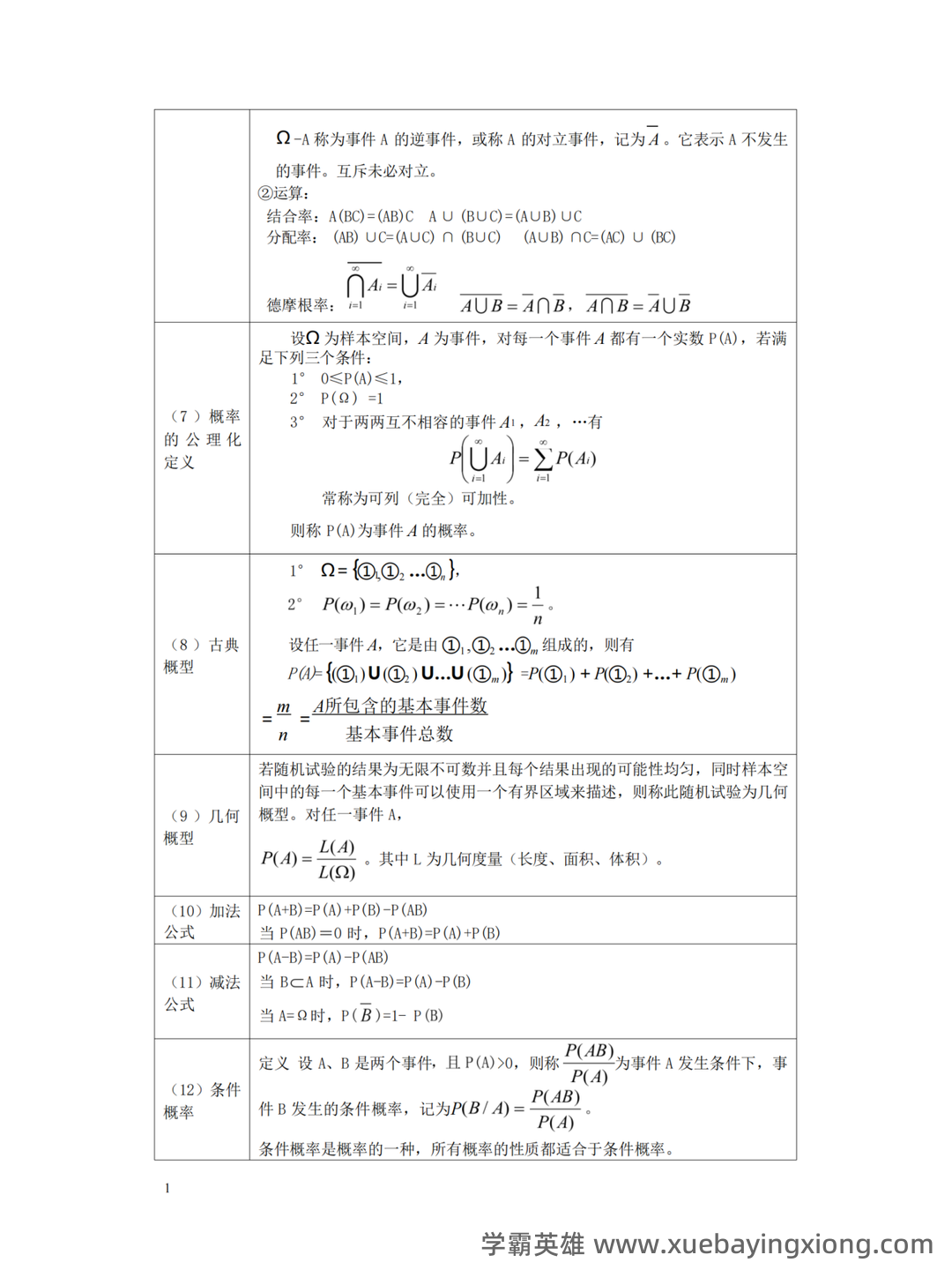
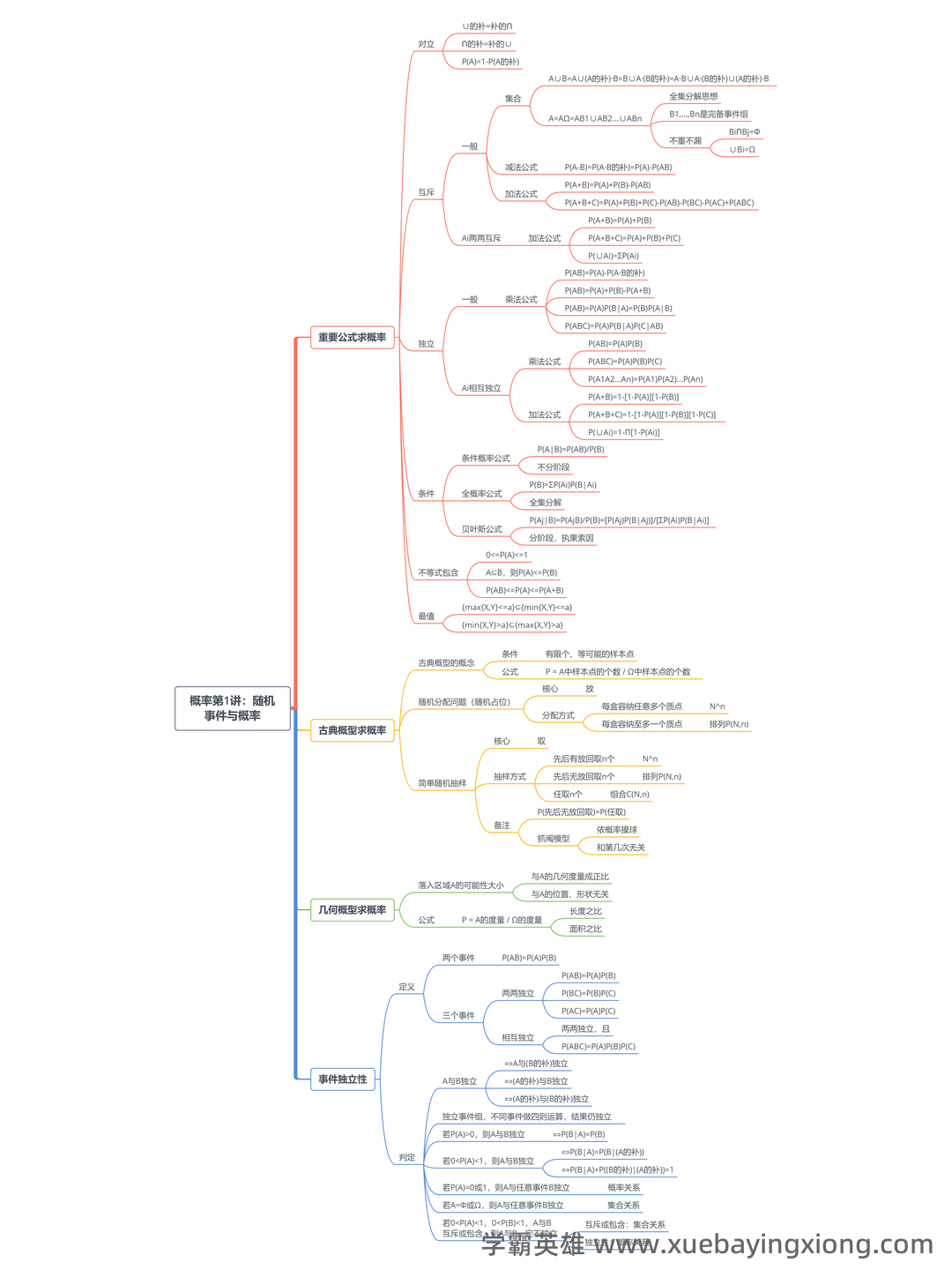
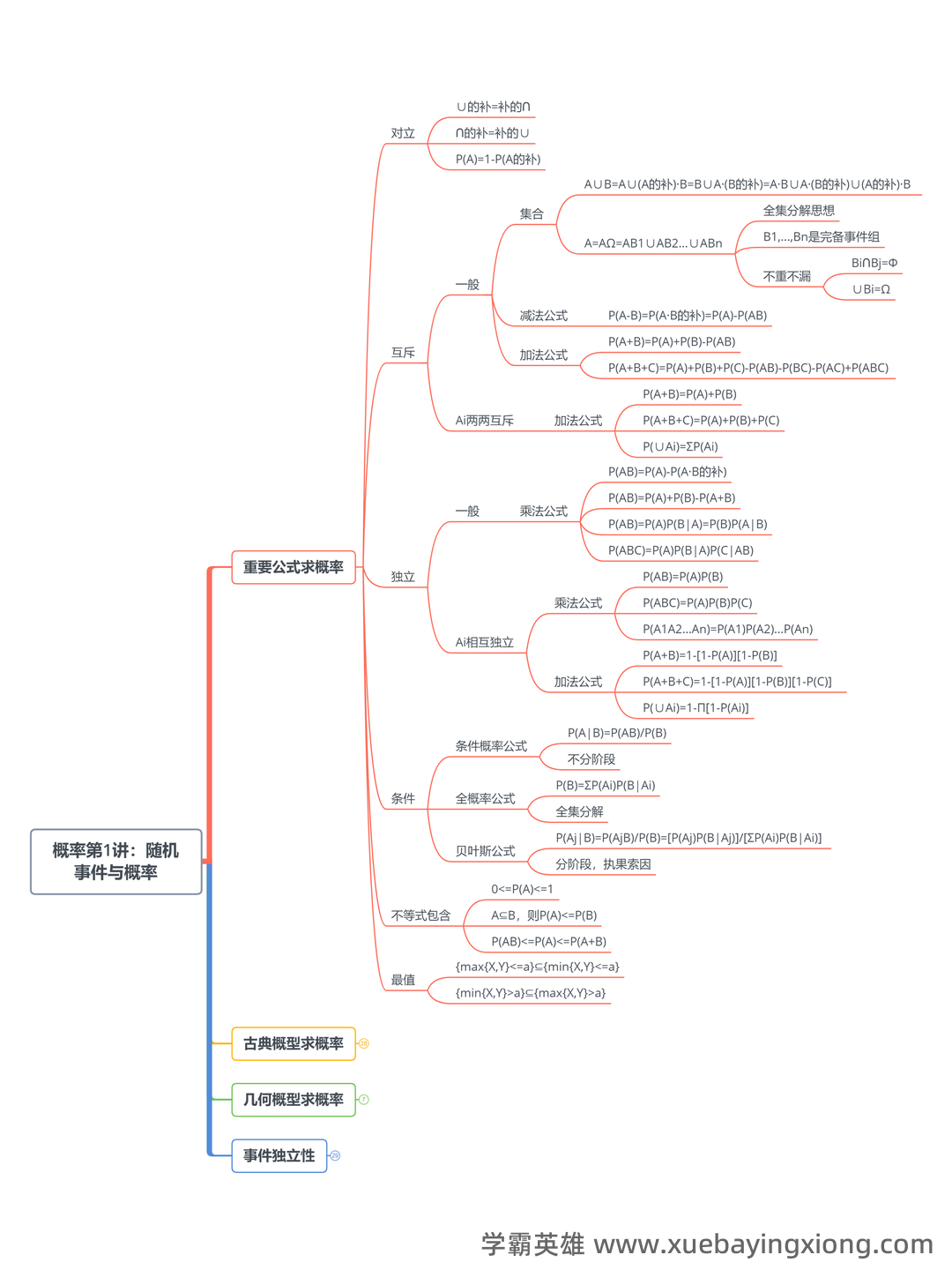
概率论-基础篇笔记(更完)_e(∑xi)=∑(exi)-CSDN 概率论，这门看似抽象的学科，其实是理解世界运行规律的基石。它从“可能性”出发，帮助我们分析和预测各种随机事件，无论是在金融、医学、工程还是人工智能领域，都能看到概率论的身影。这篇笔记旨在梳理概率论的基础知识，帮助大家快速复习，夯实理论基础。 首先，我们要理解概率的概念。概率，简单来说，就是某个事件发生的可能性大小。比如，掷一个均匀的骰子，点3的概率是1/6，因为只有6种可能的结果，且点3只有一个。 关键在于理解“可能性”这个词，它并不一定是绝对的，而是相对的，取决于我们所考虑的范围。 接下来，我们来谈谈事件。一个事件可以是某个集合中的所有元素，也可以是一个或多个集合的并集。 比如“点数大于4”这个事件，包含了骰子上的1、2、3、4、5、6中，点数大于4的数字。 然后，重点关注概率的计算。 概率的计算通常用公式表示： P(A) = n(A)/n(S)，其中 P(A)表示事件 A 的概率，n(A)表示事件 A 中元素的个数，n(S)表示总的可能结果的个数。 此外，概率论中还涉及到“总和”的概念。 Σ表示求和符号， 意味着我们要将所有相关的概率进行相加。 例如， e(∑xi) 就是对所有 x_i 的概率总和进行计算，这在统计学中至关重要。 最后，概率论的基础包括条件概率、独立事件、贝叶斯定理等。虽然这些内容稍有难度，但它们是概率论更深层理论的基础。 掌握这些基础知识，才能更好地应用概率论解决实际问题。 记住，概率论不是难学的东西，关键在于理解，多做练习，你也能成为概率论的弄潮儿！ 展开
#概率论笔记 #概率论复习 #概率论基础 #概率论笔记 #概率论学习 #概率论教程 #概率论公式
概率论
2025-07-22
11次阅读

相关文章

概率论与数理统计复习整理

概率论：从这里影响世界

考试不挂科壁纸高清概率论