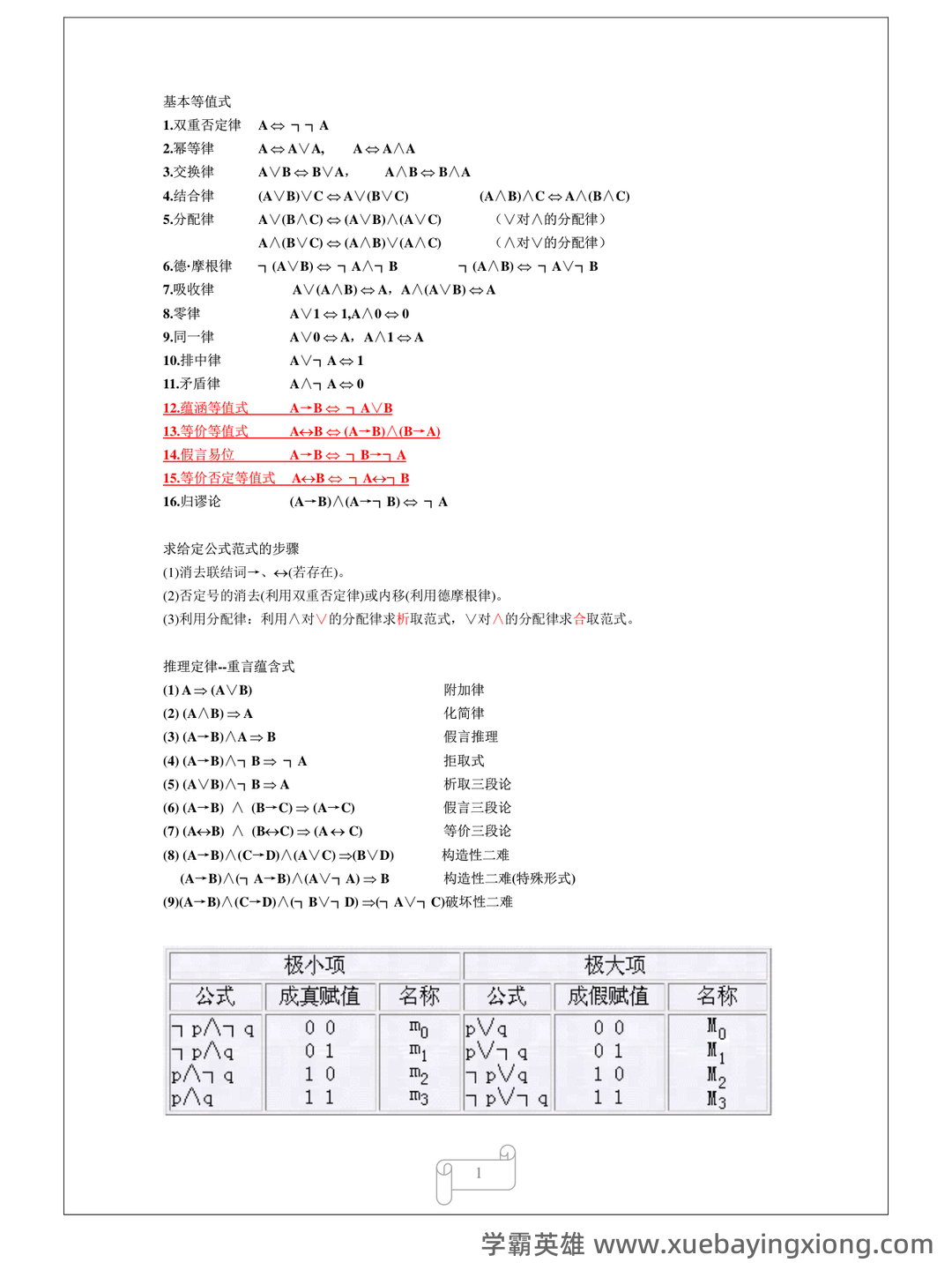
离散数学期末复习笔记精华

离散数学期末复习笔记精华 离散数学是一门研究离散对象的数学，与连续数学不同，它侧重于解决不连续问题。理解离散数学的基石在于掌握逻辑、集合、函数、命题、以及图论等核心概念。期末复习时，以下几个方面需要重点关注。 一、逻辑基础 真值表是理解命题逻辑的关键。熟练掌握否定、合取、析取等逻辑运算符及其真值表，能够有效辨析复杂命题的真假。同时，需要理解三律（非否律、德摩根定律、排中律）的应用，这对于简化逻辑表达式至关重要。 二、集合论 集合论是离散数学的基石。重点理解集合的定义、子集、并集、交集、补集等概念。掌握集合论的公理和运算规则，能够解决各种涉及集合的命题。同时，理解笛卡尔积的概念及其应用也很重要。 三、函数 函数是离散数学中的重要概念。理解函数的定义、单调性、奇偶性、复合函数等概念，能够解决涉及映射关系的各种问题。重点理解一对一、多对一、一一对应等映射的概念。 四、图论 图论是研究图的数学分支，图的基本要素包括顶点和边。重点理解图的类型（有向图、无向图、稀疏图、稠密图）、图的表示方法（邻接矩阵、邻接表）、以及基本图算法，如最短路径算法（Dijkstra、Floyd-Warshall）和最小生成树算法（Prim、Kruskal）。 五、重要公式回顾 期末复习时，务必牢记一些核心公式，例如欧拉路径公式、哈密顿路径公式、以及各类图算法的复杂度分析。 最后，多做习题，将理论知识应用于实际问题，才能真正掌握离散数学的精髓。 展开