第 1 页 / 共 34 页
第 2 页 / 共 34 页
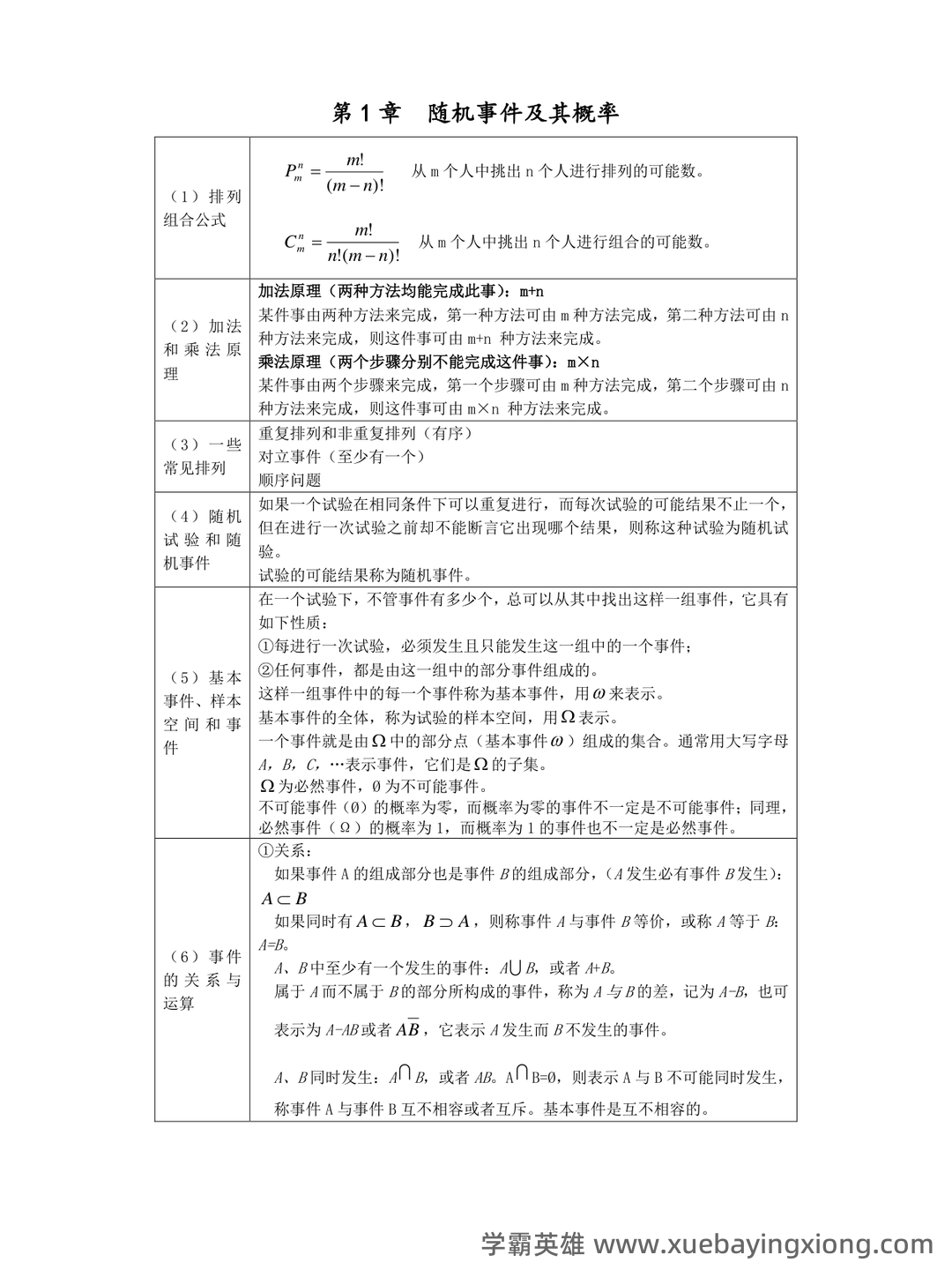
第 3 页 / 共 34 页
第 4 页 / 共 34 页
第 5 页 / 共 34 页
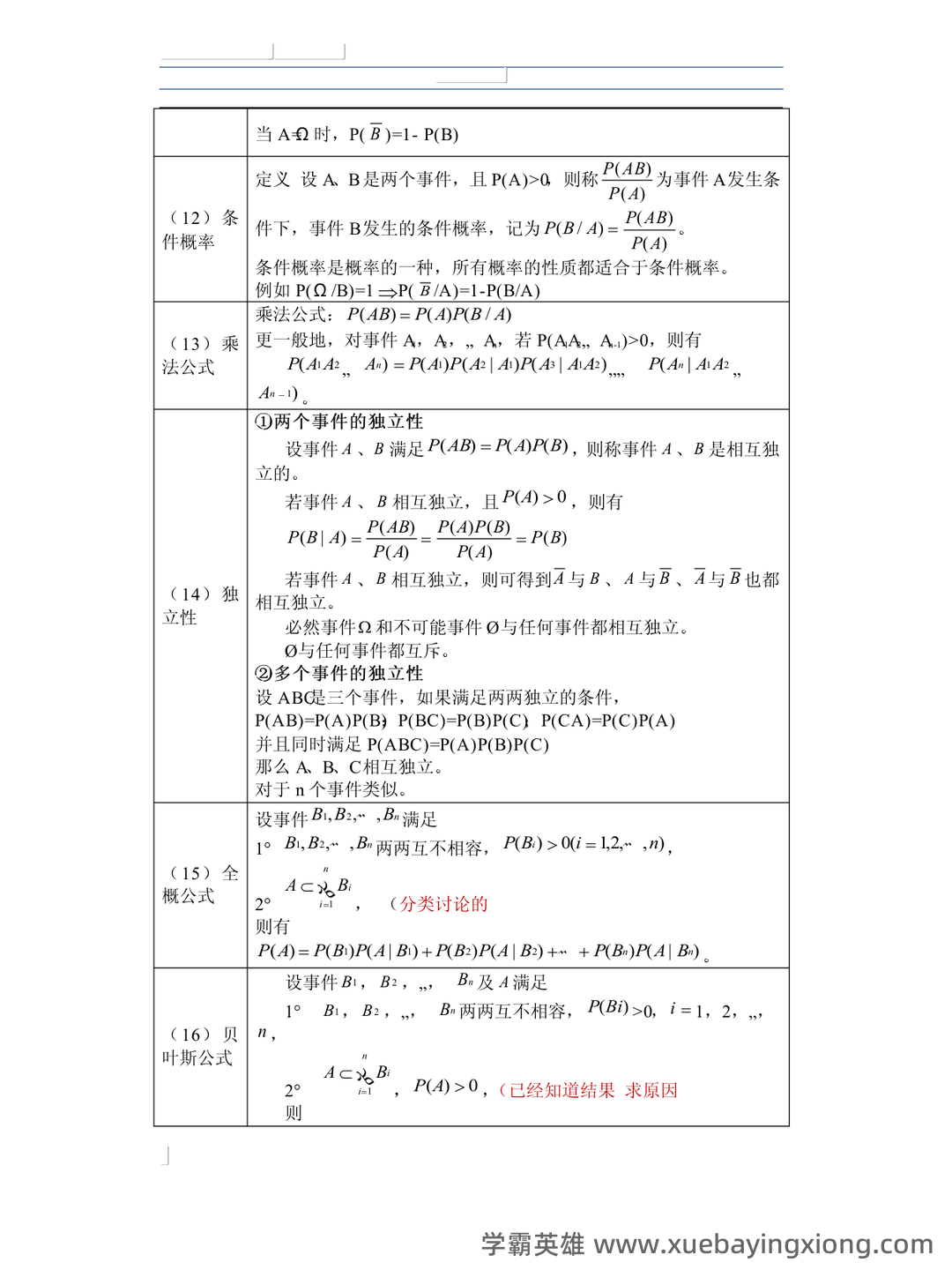
第 6 页 / 共 34 页
第 7 页 / 共 34 页
第 8 页 / 共 34 页
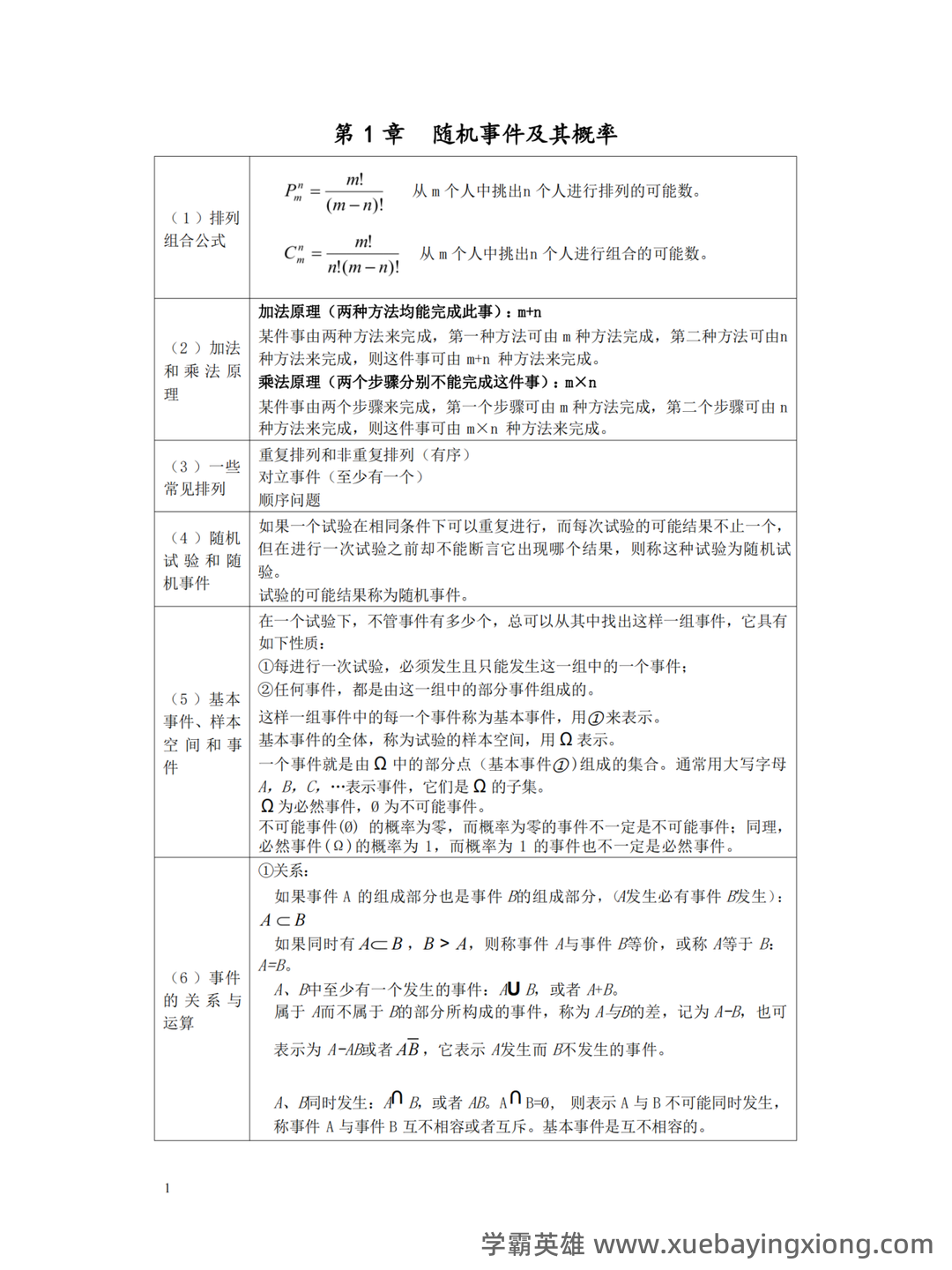
第 9 页 / 共 34 页
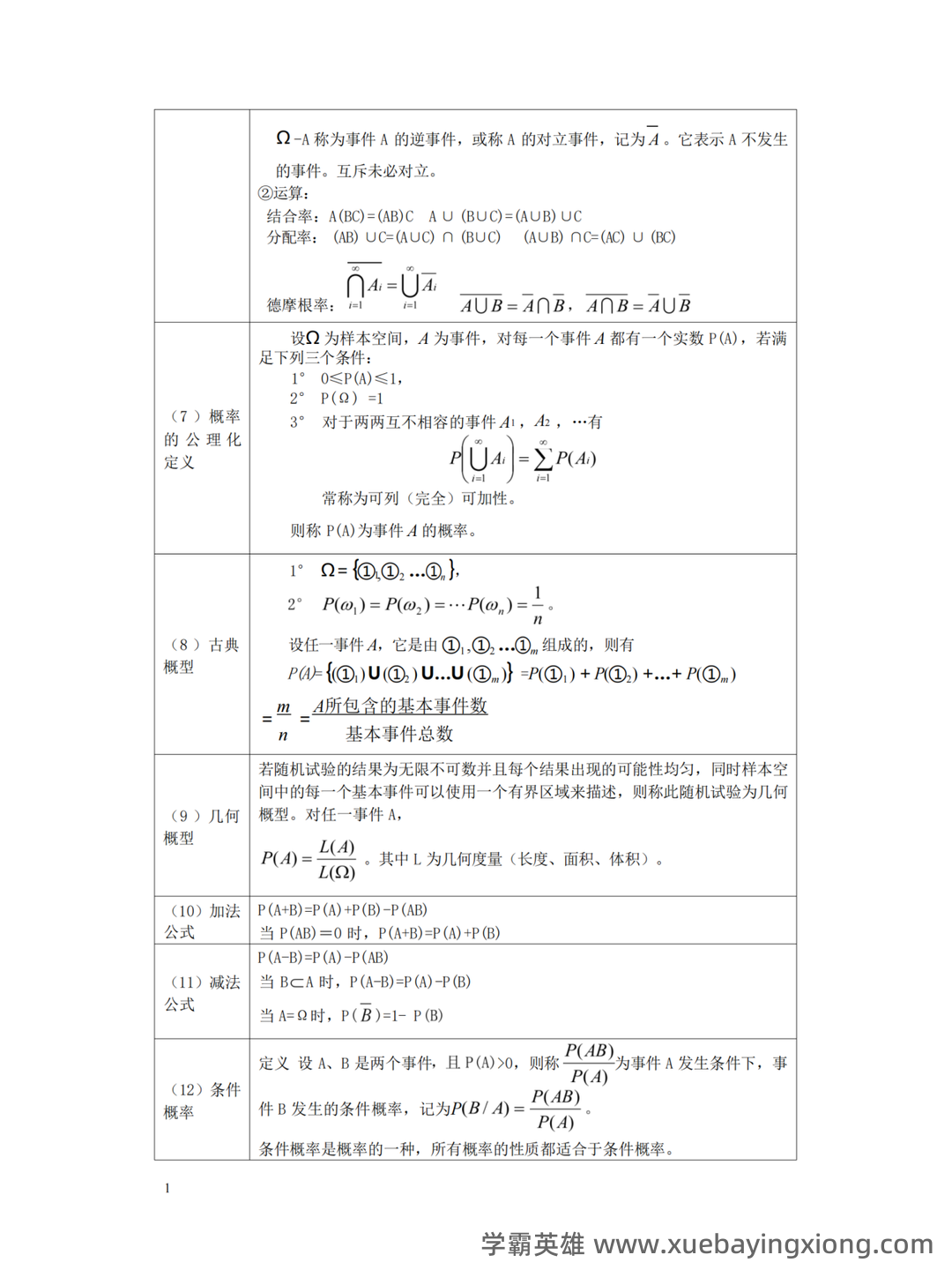
第 10 页 / 共 34 页
第 11 页 / 共 34 页
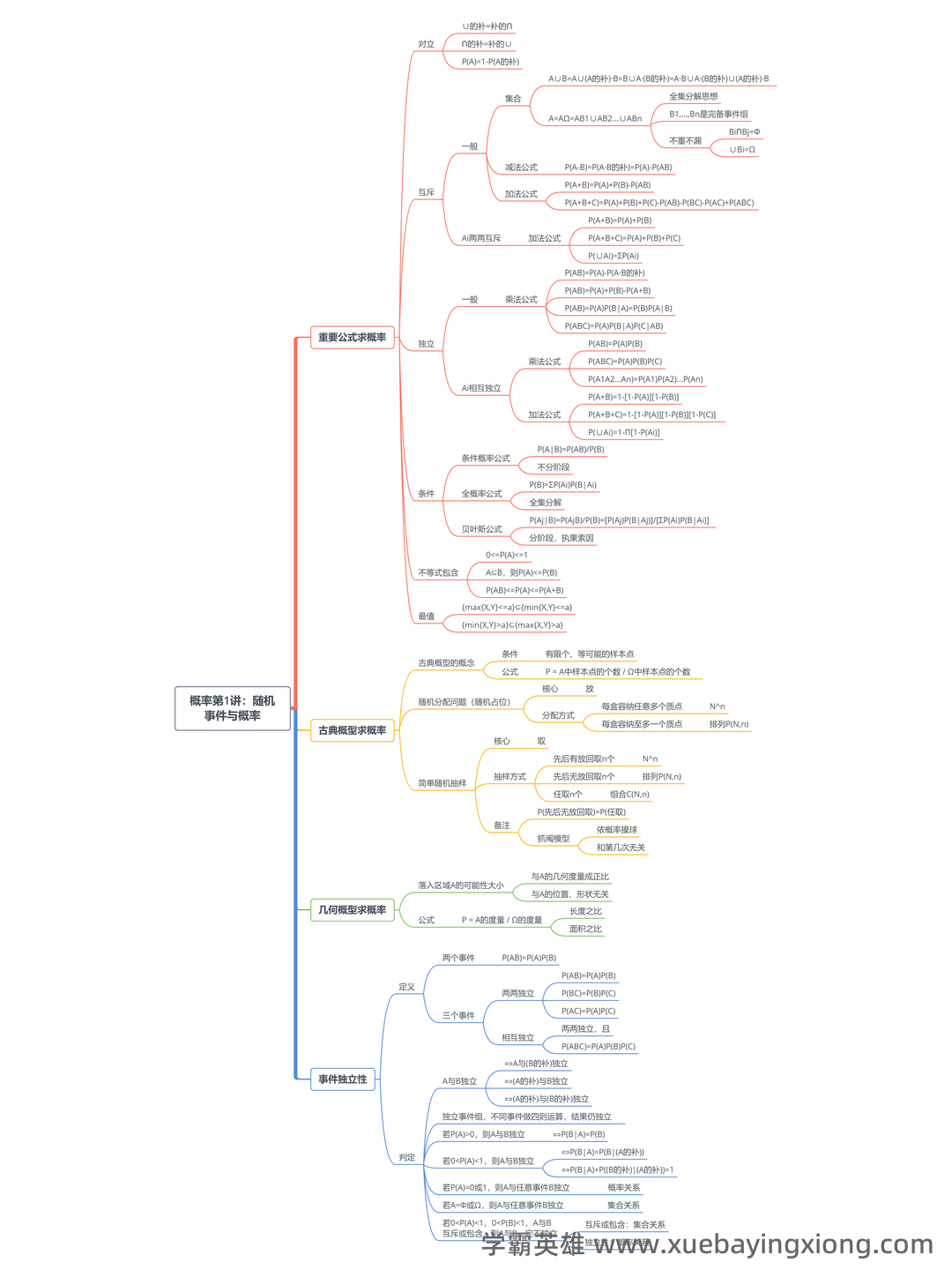
第 12 页 / 共 34 页
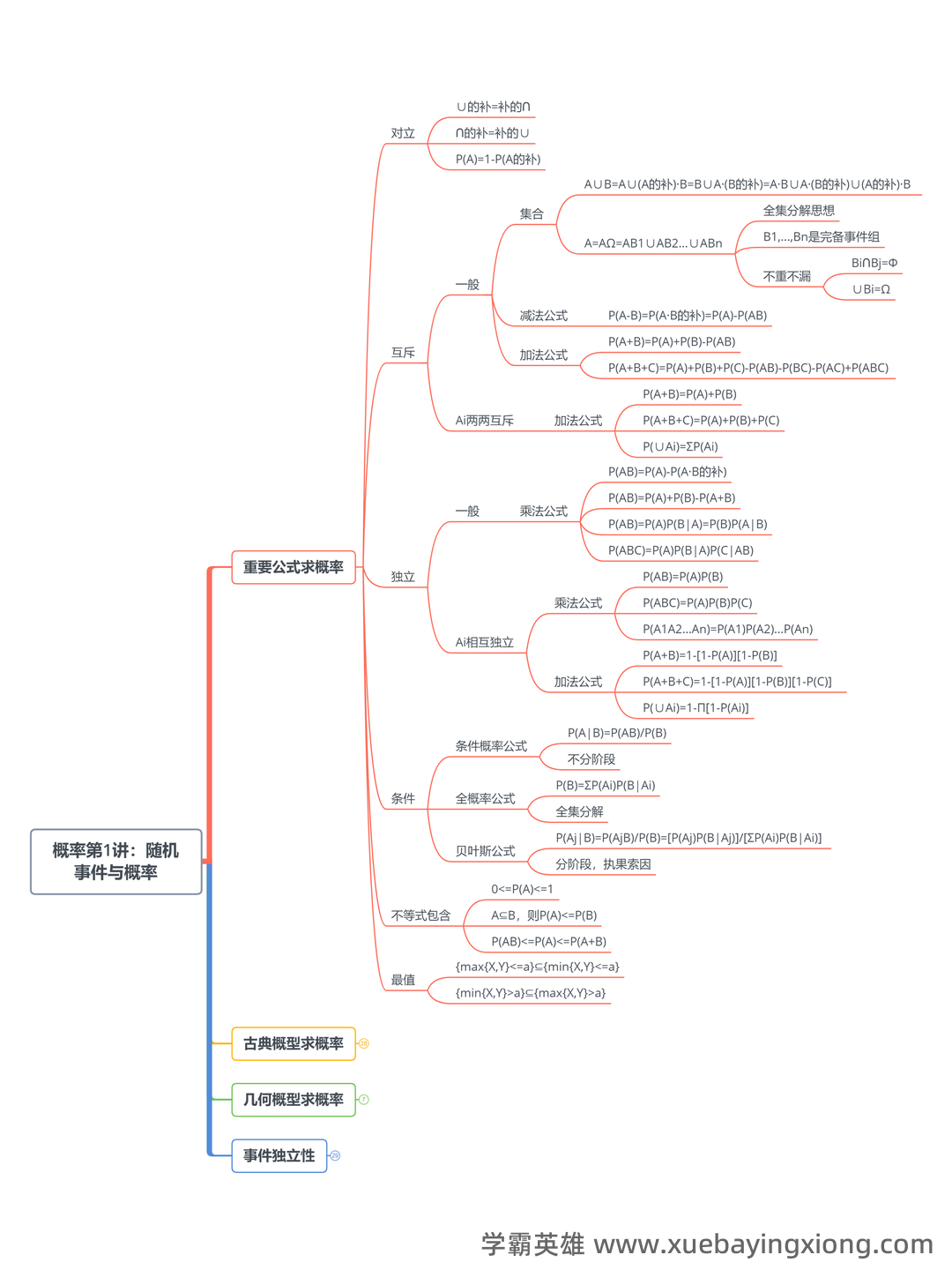
第 13 页 / 共 34 页
第 14 页 / 共 34 页
第 15 页 / 共 34 页
第 16 页 / 共 34 页
第 17 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "统计学名词解释 —— 5.「样本均值」、「样本方差」与「样本中心矩」—— 概率论与数理统计 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 18 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "统计学名词解释 —— 5.「样本均值」、「样本方差」与「样本中心矩」—— 概率论与数理统计 - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 19 页 / 共 34 页
第 20 页 / 共 34 页
第 21 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "统计学名词解释 —— 5.「样本均值」、「样本方差」与「样本中心矩」—— 概率论与数理统计 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 22 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "统计学名词解释 —— 5.「样本均值」、「样本方差」与「样本中心矩」—— 概率论与数理统计 - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 23 页 / 共 34 页
第 24 页 / 共 34 页
第 25 页 / 共 34 页
第 26 页 / 共 34 页
第 27 页 / 共 34 页
第 28 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "统计学名词解释 —— 5.「样本均值」、「样本方差」与「样本中心矩」—— 概率论与数理统计 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 29 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "统计学名词解释 —— 5.「样本均值」、「样本方差」与「样本中心矩」—— 概率论与数理统计 - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 30 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "统计学名词解释 —— 5.「样本均值」、「样本方差」与「样本中心矩」—— 概率论与数理统计 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 31 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "统计学名词解释 —— 5.「样本均值」、「样本方差」与「样本中心矩」—— 概率论与数理统计 - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 32 页 / 共 34 页
第 33 页 / 共 34 页
第 34 页 / 共 34 页
统计学名词解释 —— 5.「样本均值」、「样本方差」与「样本中心矩」—— 概率论与数理统计
统计学名词解释 —— 5.「样本均值」、「样本方差」与「样本中心矩」—— 概率论与数理统计 在概率论与数理统计中，“样本均值”、“样本方差”和“样本中心矩”是描述样本数据的三个核心概念。理解它们对于进行统计推断和分析至关重要。简单来说，它们是对总体数据的近似估计，帮助我们把握整体的特征，同时规避了获取完整总体数据的困难。 首先，样本均值（Sample Mean）就是对样本中所有观测值的平均值。概率论与数理统计中，我们经常使用样本均值来估计总体均值。例如，我们测量了10个苹果的重量，计算出它们的平均重量，这个平均重量就是样本均值，它在一定程度上可以代表所有苹果的平均重量。 接下来，样本方差（Sample Variance）衡量的是样本数据与其平均值的偏离程度的平方。 换句话说，它告诉我们样本数据离平均值的平均距离。 在概率论与数理统计中，样本方差通常用于估计总体方差，而总体方差是衡量总体数据离其均值的程度，是统计推断的基础。 最后，样本中心矩（Sample Central Moments）是样本数据围绕其中心矩的偏离程度。 相比于样本方差，中心矩可以描述更广泛的数据分布特征，例如峰值、偏度和尾部分布情况。 它在复杂的统计模型中扮演着重要的角色，尤其是在处理非正态分布数据时。 总而言之，样本均值、样本方差和样本中心矩，是概率论与数理统计工具箱中的重要组成部分，它们有效地帮助我们从有限的样本数据中提取有价值的信息，进而做出合理的决策。 掌握这些概念，是学习统计学的基础。
展开
概率论与数理统计
2025-08-06
1次阅读
资料获取方式
温馨提示：登录学霸英雄官网后可获取更多大学生必备科目和考证等复习备考资料！