第 1 页 / 共 34 页
第 2 页 / 共 34 页
第 3 页 / 共 34 页
第 4 页 / 共 34 页
第 5 页 / 共 34 页
第 6 页 / 共 34 页
第 7 页 / 共 34 页
第 8 页 / 共 34 页
第 9 页 / 共 34 页
第 10 页 / 共 34 页
第 11 页 / 共 34 页
第 12 页 / 共 34 页
第 13 页 / 共 34 页
第 14 页 / 共 34 页
第 15 页 / 共 34 页
第 16 页 / 共 34 页
第 17 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "《概率论与数理统计》重点笔记+知识点总结+公式+试题及答案，复习考试速成资料！ - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 18 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "《概率论与数理统计》重点笔记+知识点总结+公式+试题及答案，复习考试速成资料！ - 09_《概率论与数理统计》复习资料_《概率论与数理统计》知识点(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 19 页 / 共 34 页
第 20 页 / 共 34 页
第 21 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "《概率论与数理统计》重点笔记+知识点总结+公式+试题及答案，复习考试速成资料！ - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第1页_学霸英雄_www.xuebayingxiong.com")
第 22 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "《概率论与数理统计》重点笔记+知识点总结+公式+试题及答案，复习考试速成资料！ - 11_《概率论与数理统计》复习资料_《概率论与数理统计》知识点总结(详细)_第2页_学霸英雄_www.xuebayingxiong.com")
第 23 页 / 共 34 页
第 24 页 / 共 34 页
第 25 页 / 共 34 页
第 26 页 / 共 34 页
第 27 页 / 共 34 页
第 28 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "《概率论与数理统计》重点笔记+知识点总结+公式+试题及答案，复习考试速成资料！ - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 29 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "《概率论与数理统计》重点笔记+知识点总结+公式+试题及答案，复习考试速成资料！ - 15_《概率论与数理统计》复习资料_《概率论与数理统计》练(含答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 30 页 / 共 34 页
_第1页_学霸英雄_www.xuebayingxiong.com.png "《概率论与数理统计》重点笔记+知识点总结+公式+试题及答案，复习考试速成资料！ - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第1页_学霸英雄_www.xuebayingxiong.com")
第 31 页 / 共 34 页
_第2页_学霸英雄_www.xuebayingxiong.com.png "《概率论与数理统计》重点笔记+知识点总结+公式+试题及答案，复习考试速成资料！ - 16_《概率论与数理统计》复习资料_《概率论与数理统计》练(附答案)_第2页_学霸英雄_www.xuebayingxiong.com")
第 32 页 / 共 34 页
第 33 页 / 共 34 页
第 34 页 / 共 34 页
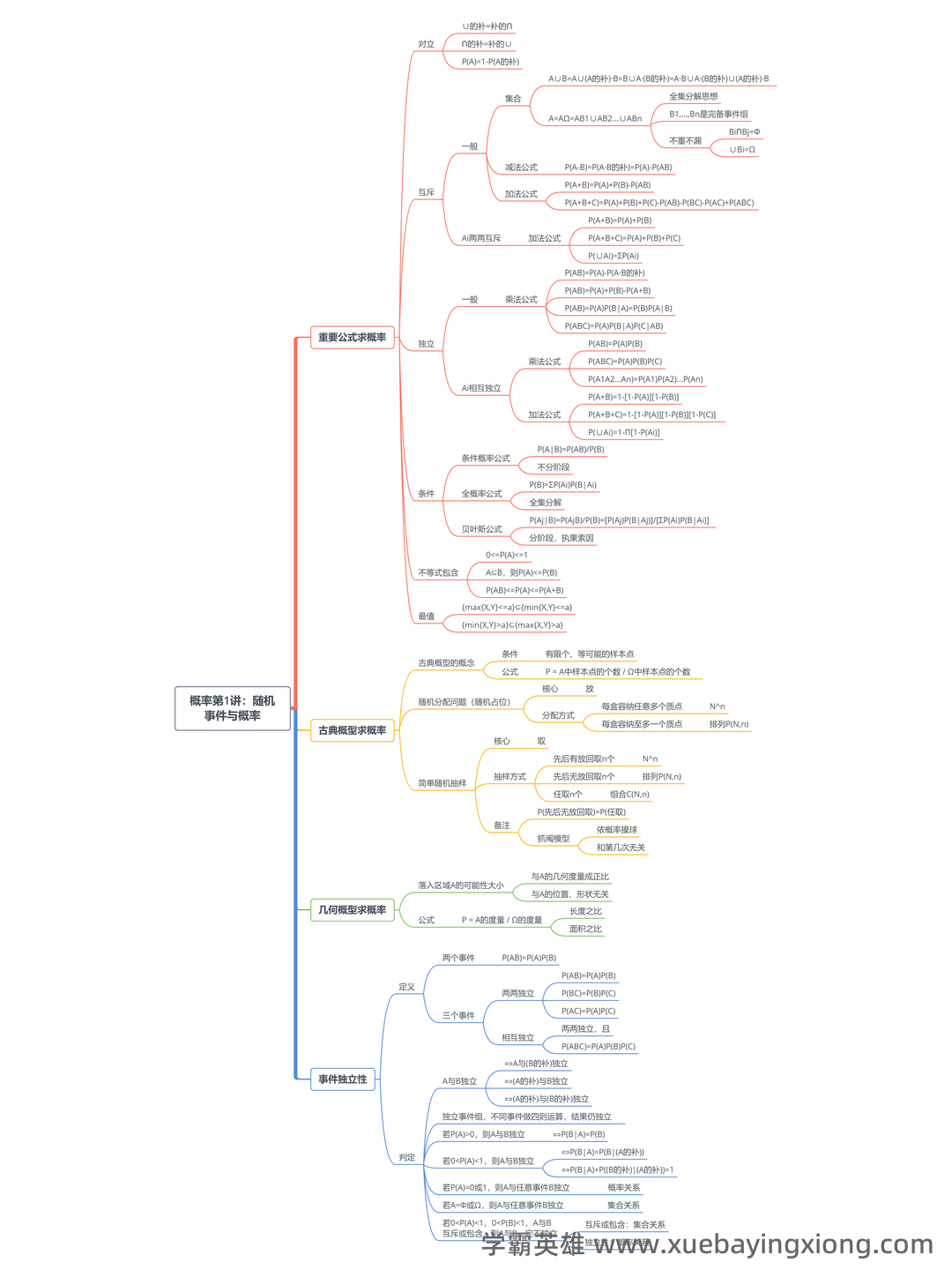
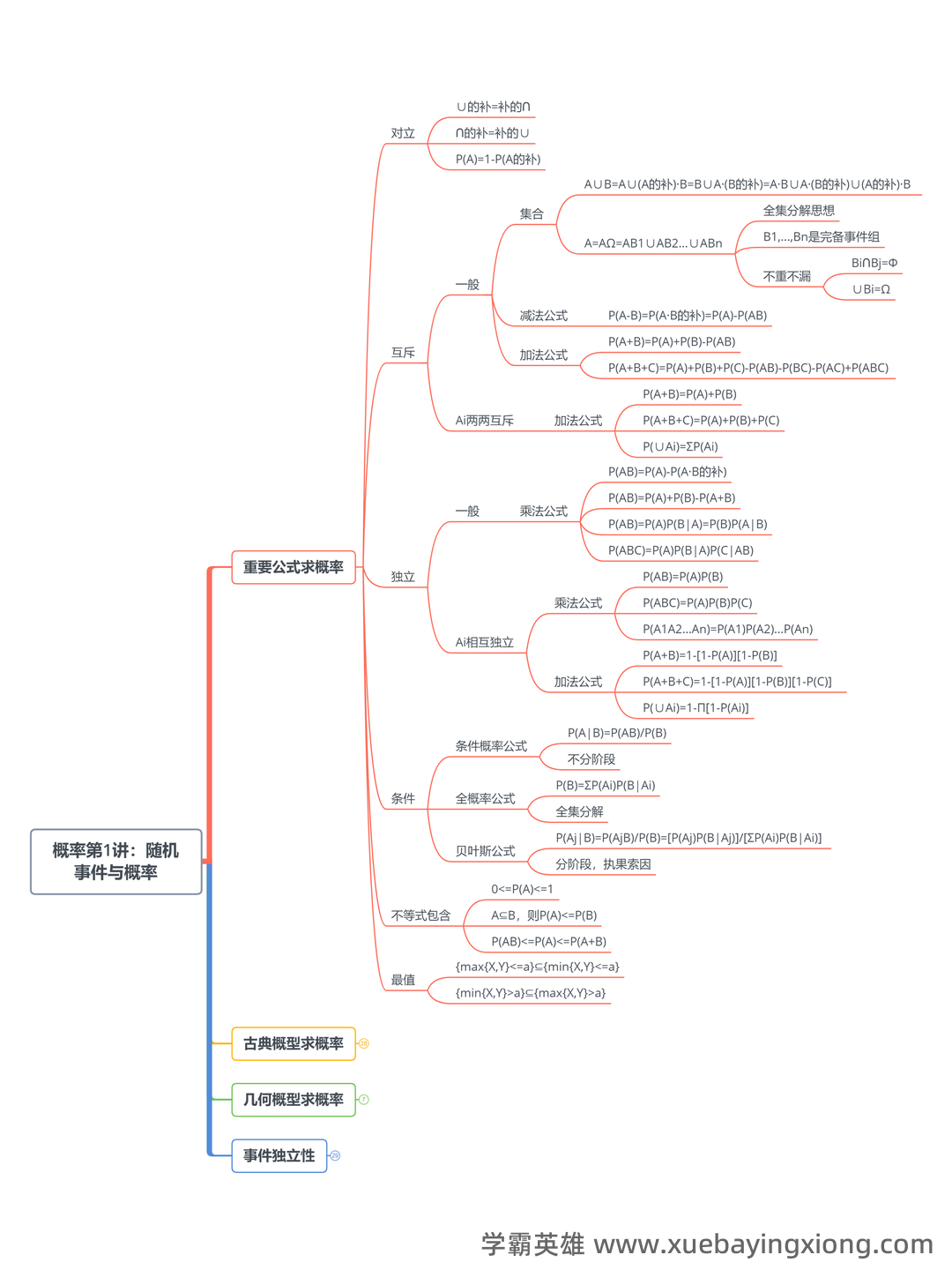
《概率论与数理统计》重点笔记+知识点总结+公式+试题及答案，复习考试速成资料！
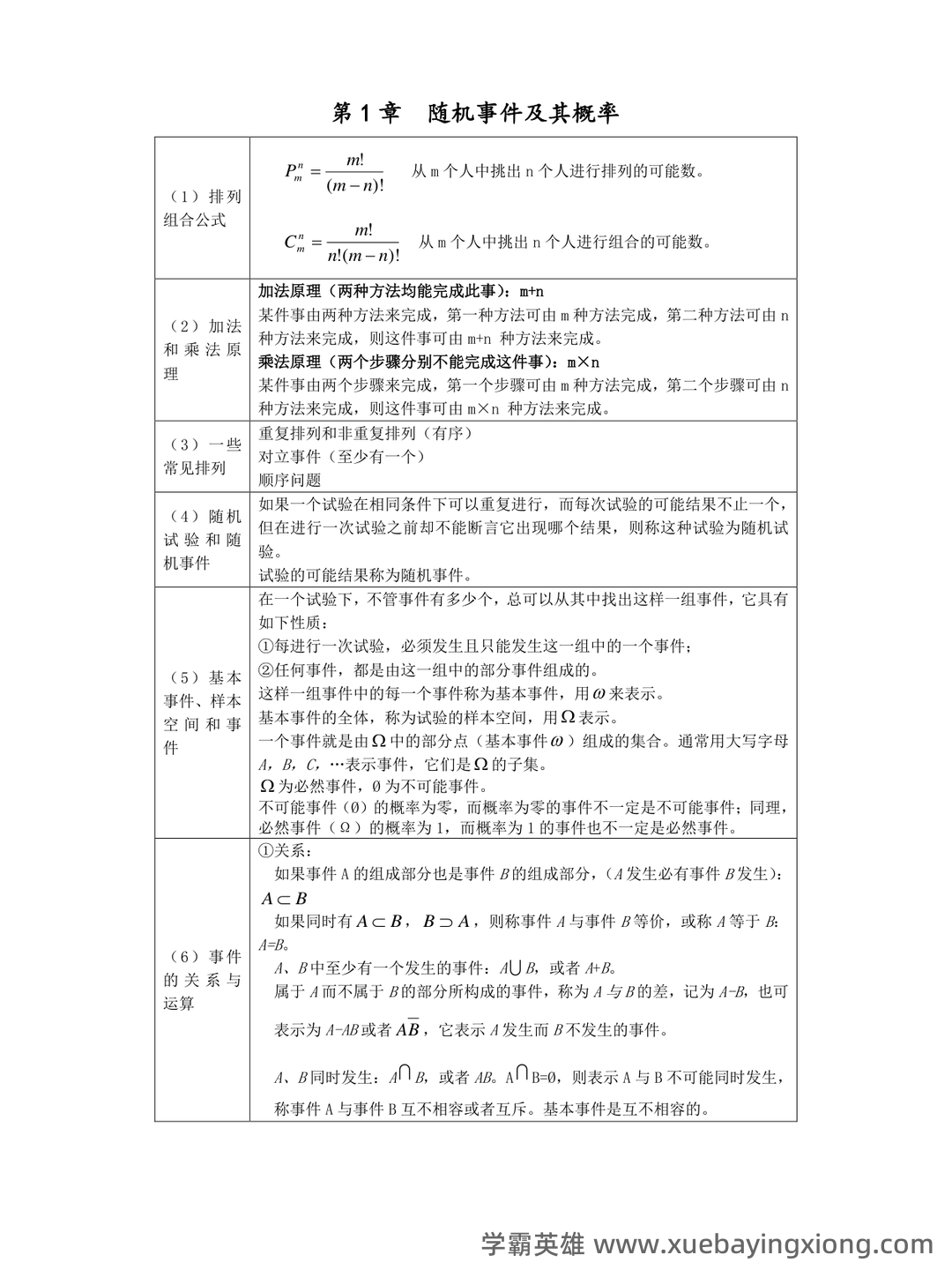
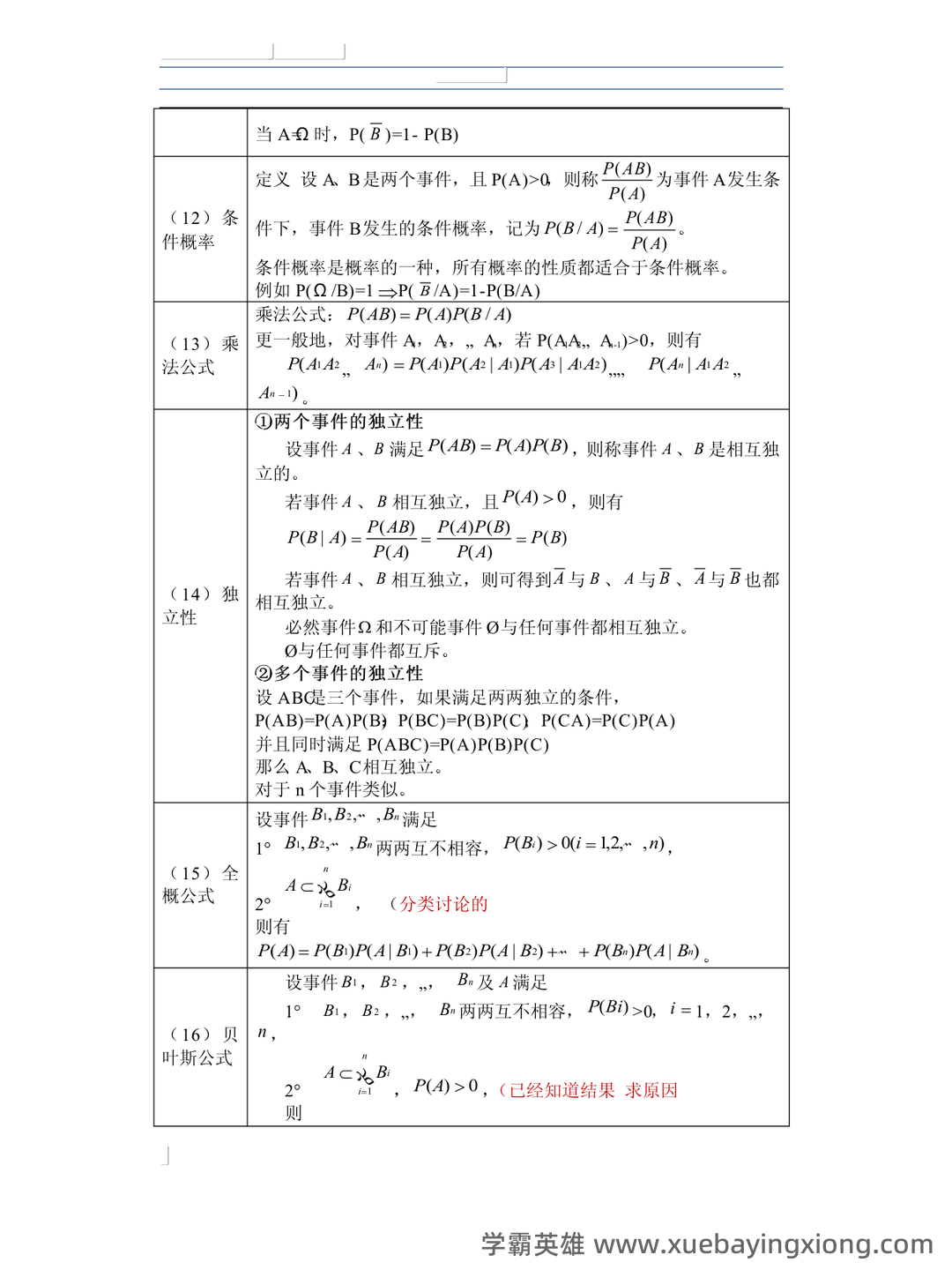
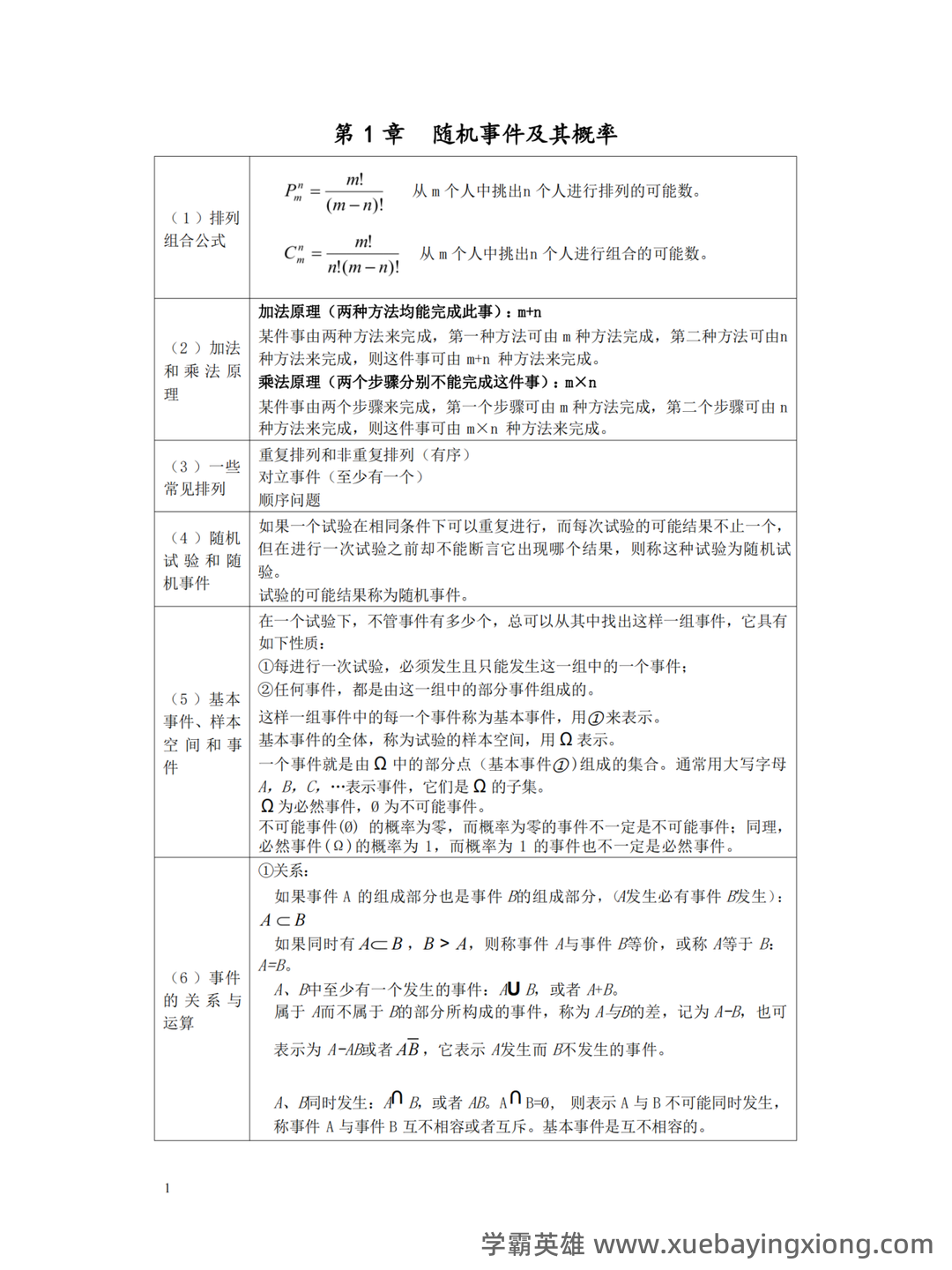
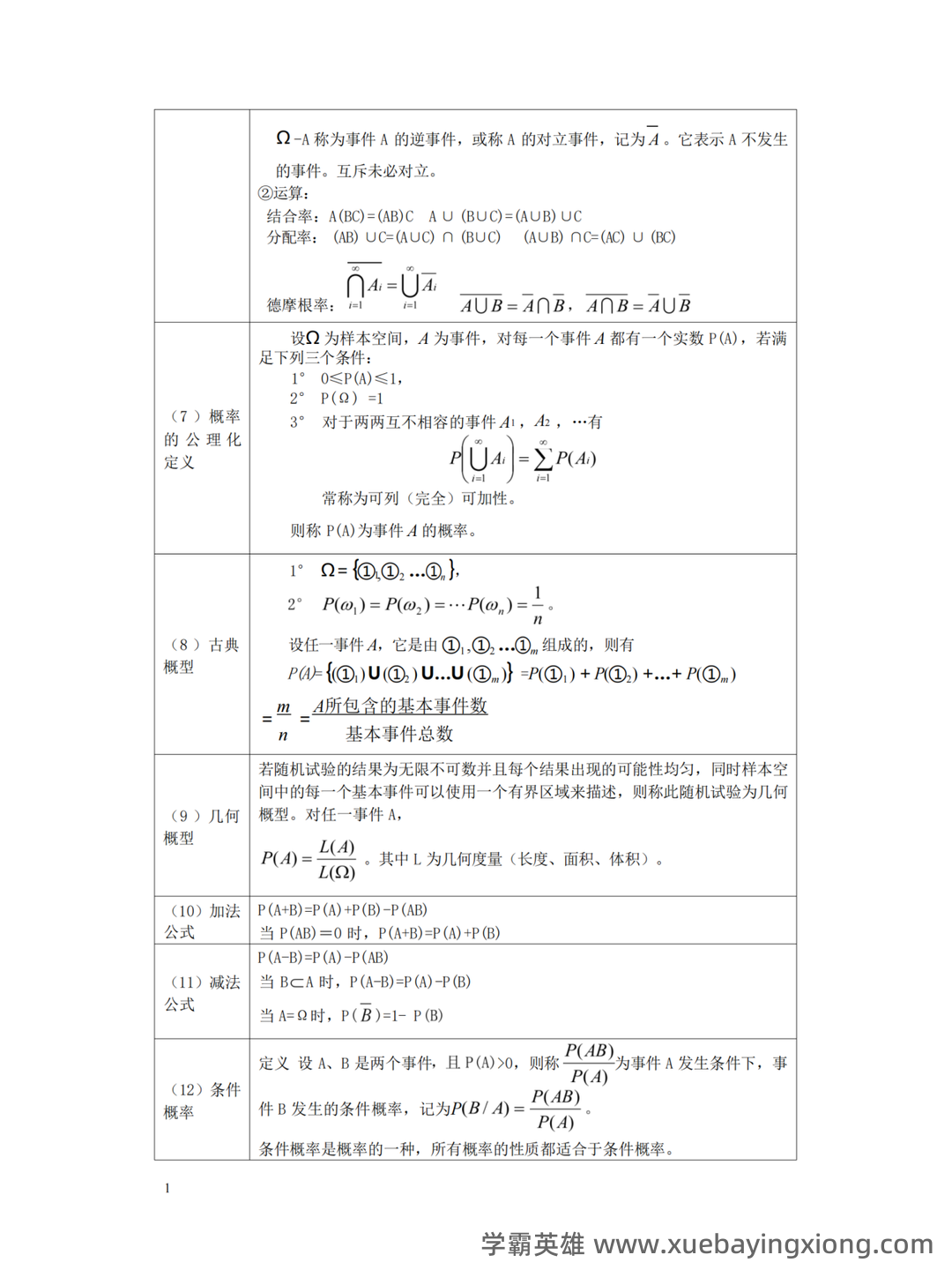
概率论与数理统计 想考好概率论与数理统计，这套速成资料绝对能帮你提速！它涵盖了核心知识点、关键公式，更有模拟试题及解析，让你在有限的时间内掌握考试要点。别再被复杂的理论搞得焦头烂额，跟着我们一步步拆解，轻松应对挑战。 首先，我们要明白概率论的核心在于概率的定义和应用。概率，简单来说，就是事件发生的可能性大小的量度。它总是介于0和1之间，0代表不可能，1代表必然。理解概率的计算方法至关重要，比如古典概型（如抛硬币、掷骰子），其概率计算直接依赖于样本空间中每个事件的概率相等。 随后，我们将深入探讨条件概率、贝叶斯定理和独立事件等核心概念。贝叶斯定理，公式为 P(A|B) = [P(B|A) P(A)] / P(B)，是概率论中最具实用价值的公式之一，它告诉我们如何在已知某些条件发生的情况下，重新评估某个事件的概率。独立事件的概率乘积是理解相关性的一大关键。 再来看看一些常用的公式：期望值的公式 E(X) = Σ[x P(x)]，方差的公式 Var(X) = E[(X-E(X))^2] ， 协方差的公式 Cov(X, Y) = E[(X-E(X))(Y-E(Y))]。 掌握这些公式，能帮助你更深入地理解数据的分布和相关性。 最后，附上几道模拟试题和答案： 例题1: 已知一个袋子里有3个红球和5个白球，随机取出一个球，求取到白球的概率。 答案: P(白球) = 5/8 = 0.625 例题2: 如果A和B两个事件不独立，且P(A) = 0.4， P(B) = 0.5， P(A∩B) = 0.2，求P(A|B)。 答案: P(A|B) = [P(B|A) P(A)] / P(B) = [P(B|A) 0.4] / 0.5 祝你复习顺利，考试一帆风顺！
展开
概率论与数理统计
2025-08-06
3次阅读
资料获取方式
温馨提示：登录学霸英雄官网后可获取更多大学生必备科目和考证等复习备考资料！